풀이

1. 문제에서 로마 문자의 순서는 중요하지 않고, 개별로 각각 더해서 계산한다고 했다. 즉, [1 5] 로 나오는 경우와 [5 1]로 나오는 경우가 같은 의미라는 것이다. (편의상 로마자는 숫자로 대체했습니다.)
2. 시간 복잡도를 미리 생각해보면, 시간 제한 2초는 2억개의 경우까지 탐색하는 것이 가능하다는 것이고, 완전탐색 (브루트포스)로 탐색하게 되면, $N=20$일 때, $4^N=2^{40}$ 을 의미하고 이는 시간 초과를 의미한다.
3. 즉, 특정 조건이 만족되면 그 이후는 거들떠도 보지않는 백트래킹으로 문제를 해결해야한다.
4. 앞에서부터 차례대로 숫자를 고른다고 했을 때, 뒤에오는 수를 자기보다 작은 값으로 지정할 필요는 없다.
5. 4.의 예시로 N이 3일때, [1 5] 로 시작하는 경우의 수를 탐색할때, 마지막에 1은 굳이 안가도 된다.
   [1 5 1]은 이미 [1]로 시작하는 경우에 존재하기 때문이다!!
   물론 순서는 [1 1 5]로 존재한다. 따라서, 우리는 선택하는 숫자들에 무조건 오름차순인 것으로 고르는 규칙을 세우도록 하자.
   
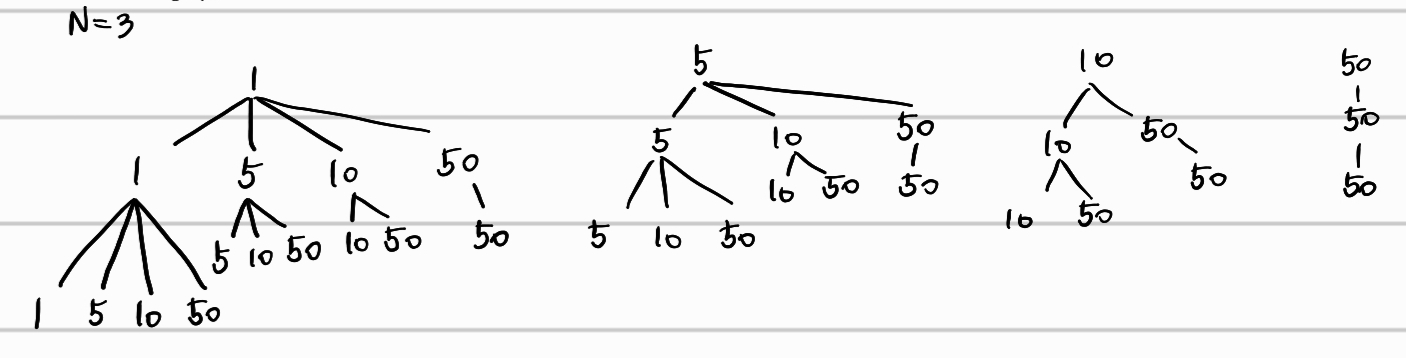
   위의 트리 구조로 보면 편하다.

# 16992 로마 숫자 만들기

N=int(input()) # N : 1~20
num=[1,5,10,50]
visited=[False]*1001
answer=0
def backtracking(idx,L,sum):
    global answer
    if L==N:
        if not visited[sum]:
            visited[sum]=True
            answer+=1
            return
        
        return

    for i in range(idx,4):
        backtracking(i,L+1,sum+num[i])


backtracking(0,0,0)
print(answer)

위의 코드에서

for i in range(idx,4):
	backtracking(i,L+1,sum+num[i])

이 부분을 통해 무조건 오름차순으로 함수가 재귀호출되는 것을 알 수 있다. 실제로 동작과정은 아래와 같다.

일부분을 그린 것인데, i=0 일때는 방문하지 않는 것을 볼 수 있다. 쉽게 이전 layer에서보다 작은 i값은 절대 가지않는다는 것을 명심하자.

6. 마지막으로 실제 합이 등장했는지의 여부를 visited 리스트로 표현하면 된다. answer를 1 더해주면서, 실제 그 합의 값이 (1001이하인 값) 등장했는지 여부를 1로 체크해주면 이전에 같은 합을 가졌던 경우를 제외할 수 있다.