부동 소수점

김동한·2024년 8월 5일

CS

목록 보기

6/13

정수 이진법

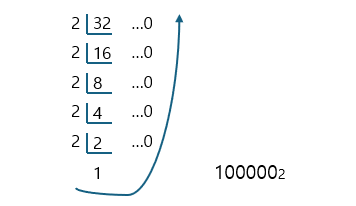
우리가 사용하는 10진수는 $10^n$ 에 해당하는 수를 기준으로 자릿수가 증가하지만, 컴퓨터는 0,1로 된 기계어를 사용한다. 10진수를 2진수로 변환하는 방법에 대해서 알아보자. 간단한 정수부터 예시로 생각해보자, $32_{10}$ 는 수의 이진 표현은 $100000_2$ 이다. 방법은 간단하다. 10진수 정수를 2로 나눠가면서 나머지를 구하다가 1이 될때까지 나누고 밑에서 거꾸로 읽으면 된다. 글로 보면 어렵지만 밑의 과정을 보면, 그렇게 어렵지않다.

하지만, 어디까지나 이는 정수에 대한 이야기다. 정수부와 소수부로 나뉘는 실수에서는 어떨까?

실수 이진법

실수범위로 확장되면, 정수부와 소수부를 포함하는 수도 표현 가능해야한다. 정수부는 위에서의 정수 이진화와 동일한 방법으로 진행한다. 소수부는 정수부에서의 이진화와 반대로 10진수에 2를 곱해가면서 1이나 0을 뽑으면 된다. 0이 나오면 종료하고, 위에서부터 결과를 읽어준다. 0.625를 이진수로 변환해보자.

$0.625\times 2=1.25$ → 1 추출 후 0.25로 다시 진행

$0.25\times 2=0.5$ → 0 추출 후 0.5로 다시 진행

$0.5\times 2=1.0$ → 1 추출 후 나머지 0

위 과정을 거쳐 나머지가 0이기 때문에, 변환을 종료하면 $0.625_{10}$ → $0.101_2$ 이 된다. 예를 들어, 실수 $32.625_{10}$ 가 주어지면, $1000000.101_2$ 로 변환된다. 10진수 기준으로 길지 않은 소수부가 2진수로 바뀌면 엄청 길어질 수 있다. 위의 예시는 $\frac n {2의 배수}$ 꼴의 분수로 예쁘게 표현되는 예시이다.

📌 2진수 변환시, 순환소수가 되며 벌어지는 일에 대해 자세하고 쉽게 설명해주신 코딩애플님의 영상 하나를 링크 해뒀다.

고정 소수점

쉽게 고정 소수점 표현 방식은 10진수를 2진수로 바꿔 그대로 넣는 방식이다. $7.625_{10}$ 는 $111.101_2$ 로 변환된다. 이를 아래와 같이 저장한다.

부호는 0→양수 1→음수를 뜻한다. 소수점의 위치는 미리 정해져있는 것으로 이동하지 않는다. 구현은 편하지만 사용하는 비트 수에 비해 표현할 수 있는 수의 범위와 정밀도가 낮다.

부동 소수점

부동 소수점에서는 그대로 수를 넣지 않고, 2진수로 변환한 결과에 추가로 정규화를 거친다.

정규화
여기서의 정규화 과정에선 2진수를 $1.$ xx $...\times 2^n$ 꼴로 변환하는 것을 말한다. 정수부에 1만 남을 때까지 소수점을 왼쪽이나 오른쪽으로 이동한다. 그리고 이동한 칸 수 만큼 n자리에 넣는다. 위의 $111.101_2$ 예시는, 정규화 과정을 거쳐서 $1.11101_2\times 2^2$ 가 된다.

IEEE 표준에 따르면, 실수를 저장하는데 32 비트(float)와 64 비트(double)를 사용하고, 32비트 기준 아래와 같은 구조를 가진다.

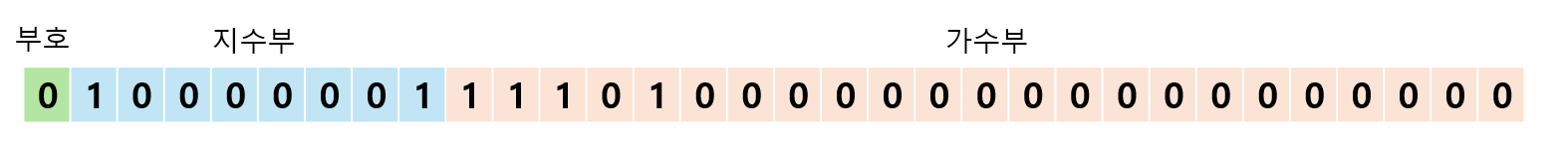
가수부 부분에 정규화 과정을 거친이후의 소수점 오른쪽의 숫자들을 그대로 넣는다. (남은 자리는 0)

지수부 붑분에는 n에 해당하는 값을 2진수로 바꾼 수를 넣는다. 이는 '10'이다 하지만 실제로 들어간 값은 다르다. 그 이유는 bias 때문이다. 32비트 기준 bias는 127로 규정되어있는데, 지수가 음수가 될 수 있기 때문에 더해지는 수이다. 위의 예시의 경우 2+127인 129의 이진표현이 입력된 것이다.

지수 자체에 부호를 표현하는 bit 하나를 더 부여하는 것이 아니라 일정의 threshold를 지정했다고 생각하자. 이로 써 10진수 기준 0~127 구간은 음수인 것이고, (bias를 더해도 127을 못넘으면 음수임) 128~255 구간은 양수를 표현하도록 만든 것이다.

참고로, double 자료형은 64비트 체계이고, 11비트의 지수부, 52비트의 가수부를 가진다. 그리고, bias는 1023이 된다. 2048개의 수를 표현할 수 있는 지수부를 가진다.

고정 소수점에 비해서 표현 가능한 수의 범위와 정밀도 측면에 우위가 있어, 정규화 과정을 거친 후, 실수를 표현하는 방식을 대부분의 컴퓨터 시스템에서 사용한다.