신장 트리
신장 트리는 모든 노드를 포함하면서, 사이클이 존재하지 않는 그래프를 의미한다. 이는 트리의 성립 조건이기도 하다.
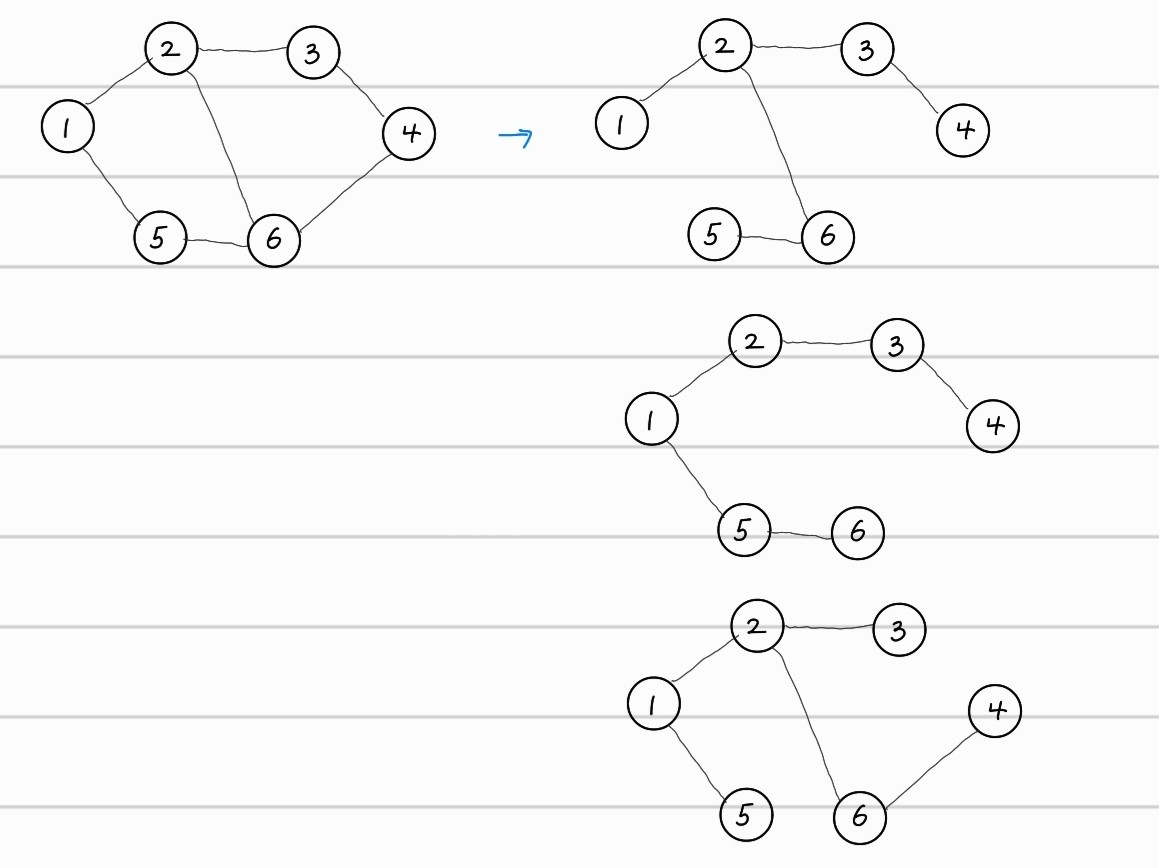
위와 같이 모든 노드를 포함하고, 사이클이 존재하지않는 것을 신장 트리라고 하며, 한개의 그래프에서 여러개의 신장트리가 존재할 수 있다.
크루스칼 알고리즘
최소한의 비용으로 신장 트리를 찾아야 할 때가 있다.
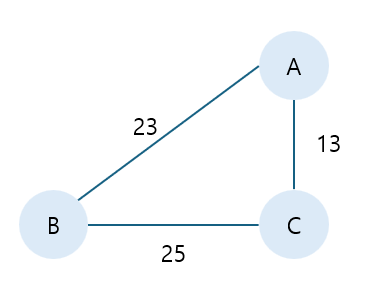
위처럼 3개의 도시 A,B,C가 있고 각 도시를 잇는 도로가 있다고 생각해보자. 최소한의 비용으로 모든 도시를 연결하려면 어떻게 해야할까? 위는 간단한 경우라서, 실제 경우의 수들을 계산할 수 있다.
- 23+13=36
- 23+25=48
- 13+25=38
이렇게 세가지 경로가 가능하고, 최종적으로, 아래와 같이 연결한 경우가 최소한의 비용이 드는 것을 알 수 있다.
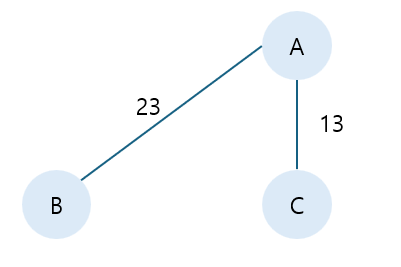
위처럼 간단한 경우는 다 세볼수 있지만, 노드와 간선의 개수가 많아지면 모든 경우를 count하기 힘들다. 따라서, 최소 비용으로 만들 수 있는 신장트리를 찾는 알고리즘인 크루스칼 알고리즘이 사용된다.
크루스칼 알고리즘은 그리디 알고리즘으로 분류된다. 모든 간선에 대해서 정렬을 수행한 후, 거리가 짧은 간선부터 집합에 포함시킨다.
- 간선 데이터를 비용에 따라 오름차순으로 정렬한다.
- 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인한다.
2.1 사이클이 발생하지 않는 경우 최소 신장 트리에 포함시킨다.
2.2 사이클이 발생하는 경우 최소 신장 트리에 포함시키지 않는다.- 모든 간선에 대해 2번 과정을 반복한다.
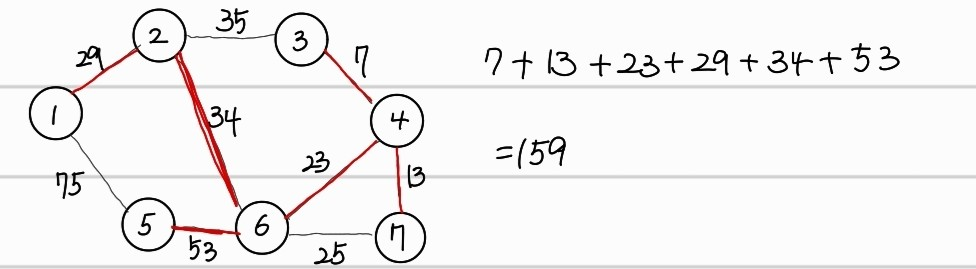
최종적으로 최소 신장 트리에 포함되는 간선의 개수가 '노드의 개수-1' 과 같다는 특징이 있다. 크루스칼 알고리즘의 핵심원리는 사이클을 이루는 간선을 제외하고 최소 비용의 간선을 집합에 추가하는 것이다. 단계별로 확인해보자.
크루스칼 알고리즘 동작 과정
실제로는 전체 간선 데이터를 리스트에 담은 후 정렬한 상태로 존재하지만, 가독성을 위해서 노드 데이터 순서로 테이블의 데이터를 나열했다.
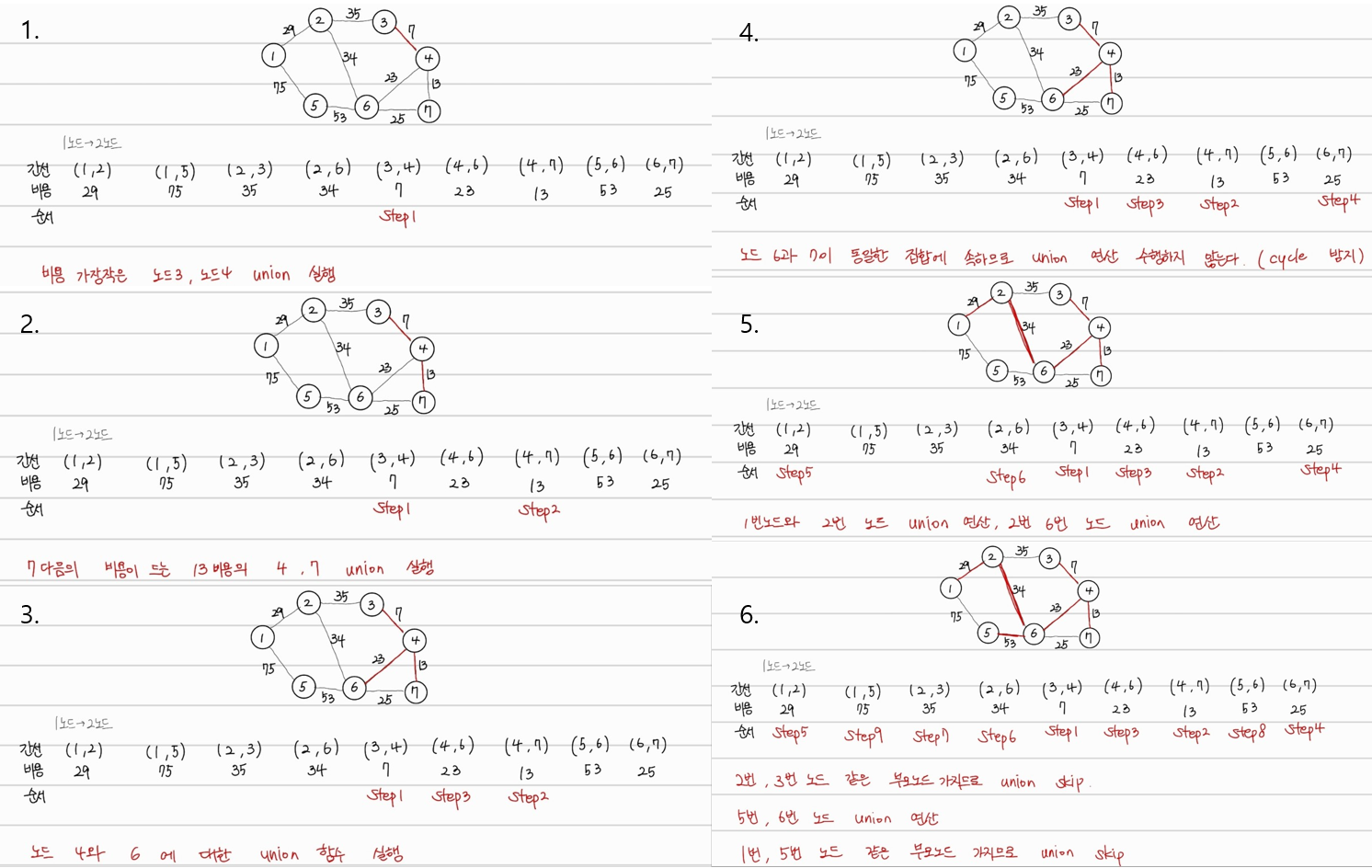
최종적으로 다음과 같은 최소신장 트리를 찾을 수 있다.
이전의 union find 코드를 응용하여 크루스칼 알고리즘을 구현하자.
- python code
def find_parent(parent,x):
if parent[x]!=x:
parent[x]=find_parent(parent,parent[x])
return parent[x] # 부모 테이블에 바로 root node 저장
def union_parent(parent,a,b):
a=find_parent(parent,a)
b=find_parent(parent,b)
if a<b: # 값이 더 작은 노드를 가리키게 트리 생성
parent[b]=a
else:
parent[a]=b
v,e=map(int,input().split())
parent=[0]*(v+1)
edges=[]
result=0 # 모든 간선 cost의 합
# 자기 자신 노드 크기로 부모 테이블 초기화
for i in range(1,v+1):
parent[i]=i
for _ in range(e):
a,b,cost=map(int,input().split())
edges.append((cost,a,b))
edges.sort() # 크루스칼 알고리즘을 위해서 데이터 정렬 꼭 해야함
for edge in edges:
cost,a,b=edge
if find_parent(parent,a)!=find_parent(parent,b):
union_parent(parent,a,b)
result+=cost
print(result)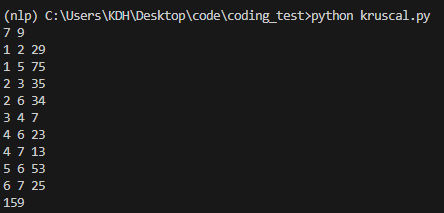
크루스칼 알고리즘은 간선의 개수가 E개 일때 의 시간 복잡도를 가진다. 이는, 알고리즘에서 시간이 가장 오래걸리는 부분이 간선을 정렬하는 작업이기 때문이다. 따라서,
edges.sort()에 해당하는, 정렬 부분이(파이썬 내장 라이브러리의 정렬 알고리즘은 을 보장한다.) 곧 해당 알고리즘의 시간 복잡도 라는 것을 알 수 있다.
Reference
이것이 취업을 위한 코딩 테스트다 with 파이썬

