위상 정렬

위상 정렬은 정렬 알고리즘의 일종이다. 순서가 정해져있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘이다. 정확히는, 방향 그래프의 모든 노드를 '방향성에 거스르지 않도록 순서대로 나열하는 것'이다.

📌 진입 차수
진입차수란 특정한 노드로 '들어오는' 간선의 개수를 의미한다.

위상 정렬 알고리즘은 아래와 같이 동작한다.

1. 진입차수가 0인 노드를 큐에 넣는다.
2. 큐가 빌 때까지 다음의 과정을 반복한다.
   2.1 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
   2.2 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.

원소가 V번 꺼내질 때까지 큐는 비어있으면 안된다. 만약 노드의 개수인 V번 만큼 큐에서 꺼내지 못했는데 큐가 빈다면, 사이클이 발생한 것을 의미한다. 기본적으로, 위상정렬을 사용할 문제는 사이클이 발생하지 않는다는 것을 명시하는 경우가 많아 크게 걱정하지 않아도 된다. 위상정렬은 아래와 같이 동작한다.

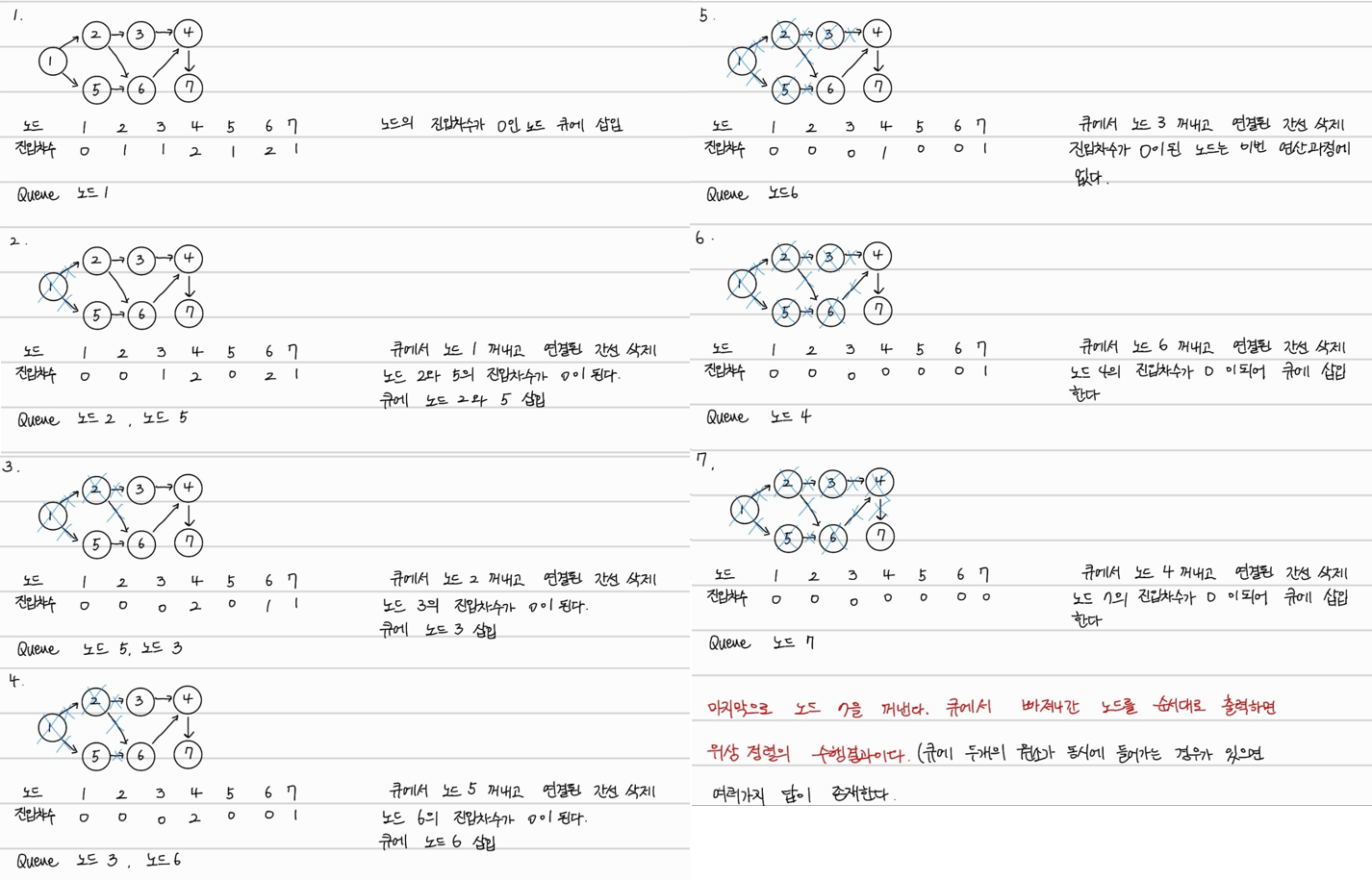
현재 진입차수가 0인 노드가 여러개 있어서 두개 이상의 노드를 한번에 큐에 입력하는 경우가 생긴다면, 어떤 노드를 먼저 넣는지에 따라서, 결과가 달라질 수 있다. 위의 예시에서도 2번 과정에서 2번 노드를 먼저 넣는지, 5번 노드를 먼저 넣는지에 따라 결과가 다르다

• 2번 노드 먼저 넣을때
  1-2-5-3-6-4-7
• 5번 노드 먼저 넣을때
  1-5-2-3-6-4-7

아래는 위상 정렬을 구현한 파이썬 코드이다.

• python code

from collections import deque

v,e=map(int,input().split())
indegree=[0]*(v+1) # node 별 진입차수

graph=[[]for i in range(v+1)]

for _ in range(e):
    a,b=map(int,input().split())
    graph[a].append(b)
    indegree[b]+=1

def topology_sort():
    result=[]
    q=deque()

    for i in range(1,v+1):
        if indegree[i]==0:
            q.append(i) #진입차수가 0인 node queue에 삽입

    while q:
        current=q.popleft()
        result.append(current)
        for i in graph[current]:
            indegree[i]-=1 # 현재 노드와 연결된 간선 삭제(진입차수 1씩 감소)
            if indegree[i]==0:
                q.append(i)

    print("위상정렬 결과: ",end="")
    for i in result:
        print(i, end=" ")

topology_sort()

위상 정렬의 시간 복잡도는 $O(V+E)$이다. 위상 정렬을 수행할 때는 차례대로 모든 노드를 확인하면서, 출발하는 간선을 차례대로 제거해야한다. 노드와 간선을 모두 확인하기 때문에 $O(V+E)$의 시간이 소요된다.

Reference

이것이 취업을 위한 코딩 테스트다 with 파이썬