다익스트라 알고리즘은 한 지점에서 다른 특정 지점까지의 최단 경로를 구해야 하는 경우 사용할 수 있는 최단 경로 알고리즘이다. 플로이드 워셜 알고리즘은, 모든 지점에서 모든 지점까지의 최단 경로를 구해야 하는 경우 사용할 수 있는 알고리즘이다.

플로이드 워셜

• 시간 복잡도 : $O(N^3)$

다익스트라 알고리즘과 다르게, 2차원 리스트에 '최단 거리' 정보를 저장한다. 모든 노드에 대해 다른 모든 노드로 가는 최단 거리 정보를 담아야하기 때문이다. N번의 단계에서 매번 $O(N^2)$의 시간이 소요되기 때문에 총 $O(N^3)$의 시간이 소요된다. 플로이드 워셜 알고리즘의 점화식은 아래와 같다.

A노드와 B노드 사이의 최단 거리는, 기존에 있던 A에서 B로 직접 이동하는 경우와 K노드를 거쳐서 이동하는 경우를 비교하여 작은 값을 최단거리로 설정한다.

각 단계에서는 어떤 노드를 거쳐 가는 지를 선택한다. 현재 확인하고 있는 노드를 제외하고 N-1개의 노드중에서 서로 다른 노드 (A,B) 쌍을 골라야한다. 예를들어, 1번 노드를 확인중이라면, 1번 노드를 제외한 노드 중에서 두개의 노드를 순서있이 고르는 모든 경우의 수를 고려해야한다. 그렇게 해야, 선택한 두 노드가 직접 연결된 경우, 선택한 두 노드 사이에 1번 노드를 방문하는 경우의 거리 차이를 계산할 수 있다.

이는 ${}_{n-1}P_2$ 개의 쌍을 확인해야한다는 것을 의미한다. 이는 $O(N^2)$의 시간이 걸리고 총 N단계 수행하기 때문에, 시간 복잡도는 $O(N^3)$으로 계산된다.

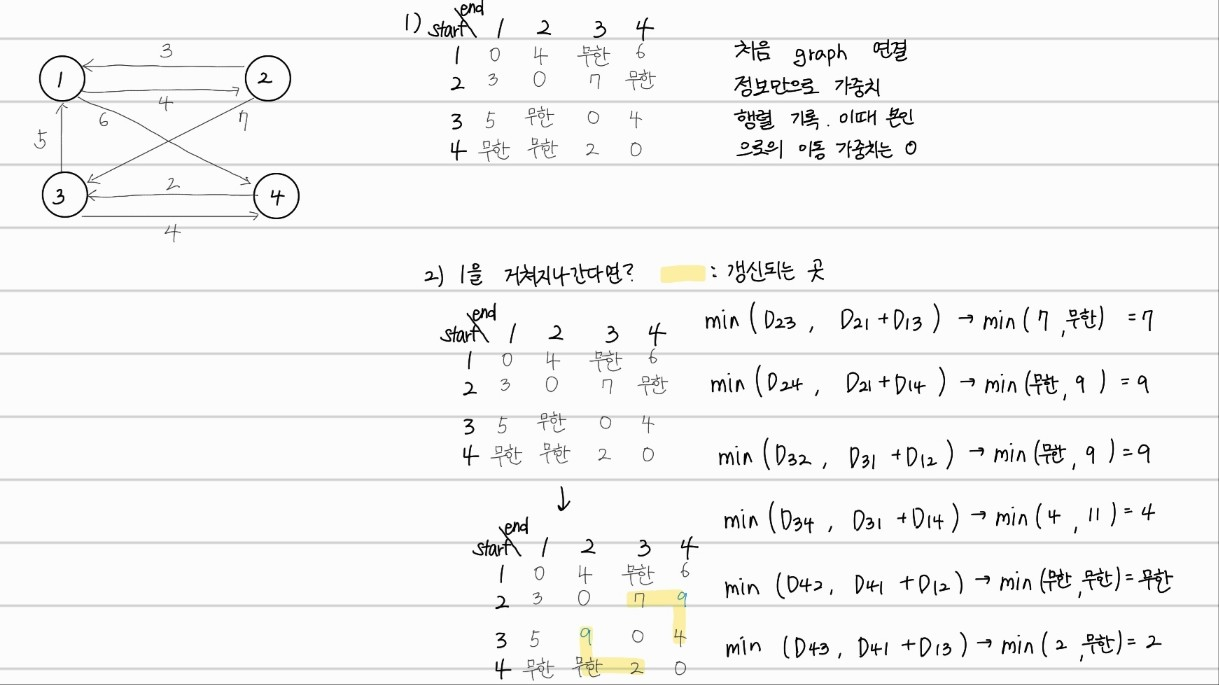
위와 같은 방법으로 진행된다. 첫번째 단계를 나타낸 그림으로, node 1을 거쳐서 지나갈때를 기준으로하여, 나머지 2,3,4번 노드를 순서를 고려하여 두개 선택하는 경우 모두에 대해서, 1을 거쳐서 가는 것이 더 작은지, 아니면 직접 가는게 더 작은지 비교하여 갱신하는 과정이다.

같은 연산을, 2번 노드 기준, 3번,4번 노드를 기준으로 해서 진행하면 최종 결과는 다음과 같다.

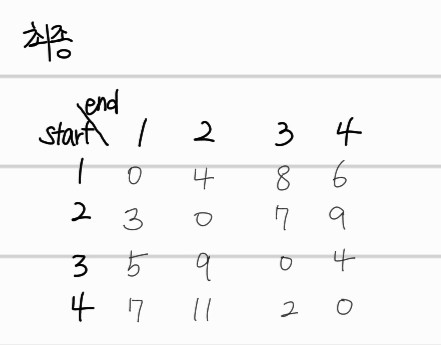
예를들어, 1번 노드에서 4번 노드로 가는 최단 거리는 6인 것이고, 4번 노드에서 2번 노드로 가는 최단 거리는 11이다. 위의 2차원 배열은 row index에서 출발해 column index에 도착할때 array[row][column] 값 즉 해당 index 위치의 value가 최단 거리를 나타낸다. 플로이드 워셜 알고리즘은, 다이나믹 프로그래밍을 다익스트라 알고리즘은 그리디 알고리즘을 기반으로 한다. 아래는 python 코드로 구현한 것이다.

• python code

INF=10000
n,m=map(int,input().split())
graph=[[INF]*(n+1) for _ in range(n+1)]
for a in range(1,n+1):
    for b in range(1,n+1):
        if a==b:
            graph[a][b]=0
            
for _ in range(m):
    a,b,c=map(int,input().split()) # a에서 b로 가는데 드는 비용 c
    graph[a][b]=c
    
for k in range(1,n+1):
    for a in range(1,n+1):
        for b in range(1,n+1):
            graph[a][b]=min(graph[a][b],graph[a][k]+graph[k][b])
            
for a in range(1,n+1):
    for b in range(1,n+1):
        if graph[a][b]==INF:
            print("INFINITY",end=" ")
            
        else:
            print(graph[a][b],end=" ")
    print()

재귀함수를 통해서 이를 구현할 수 있다. 생각보다 코드 구현은 어렵지않다. 이전에 언급한 점화식을 토대로 작성하면 된다.

Reference

이것이 취업을 위한 코딩 테스트다 with 파이썬