본 포스트는 [모두를 위한 딥러닝 시즌2] 강의를 기반으로 작성하였습니다.
Linear Regression
머신러닝에 대해 공부하다 보면, 가장 먼저 나오는 개념이 바로 Linear Regression(선형 회귀)입니다. Linear Regression이란 여러 개의 학습 데이터들이 있다고 할 때, 그 학습 데이터들을 가장 잘 나타낼 수 있는 하나의 직선을 찾는 방법입니다.
Hypothesis
이 직선은 아래의 식 처럼 나타낼 수 있습니다.
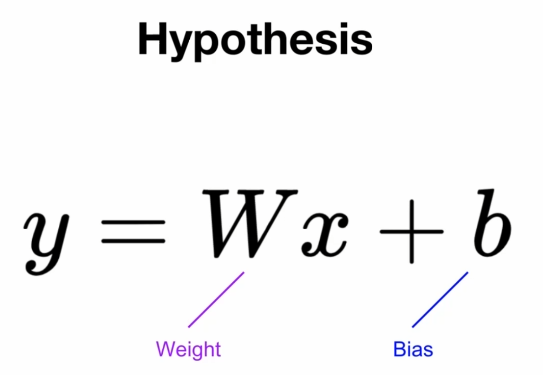
여기서 입력값 x에 곱해지는 W를 weight, 더해지는 b를 bias라고 합니다. 우리는 반복되는 기계 학습을 통해서, 데이터들을 잘 나타내는 W와 b를 찾아야 합니다.
loss
여기서 의문이 듭니다. 데이터를 잘 나타낸 다는 것을 어떻게 알 수 있을까? 기계 학습에서는 loss function(손실 함수)을 통해 확인할 수 있습니다.
SSE (Sum Squared Error)
그 중 가장 간단한 방법이 단순히 실제 값에서 예측 값을 빼서 제곱하는 방법입니다. 이 값들을 모두 더해 평가하는 방법을 SSE(Sum Squared Error)라고 합니다.
이 방식의 문제점은 값이 큰 이유를 알 수 없다는 것이다. 데이터의 양이 많아서인지, 데이터의 오차가 커서인지를 알 수 없습니다.
MSE (Mean Sqaured Error)
그래서 나온 방법이 MSE 방법입니다. 평균을 구하기 때문에, 위에 나온 문제점을 해결할 수 있습니다.
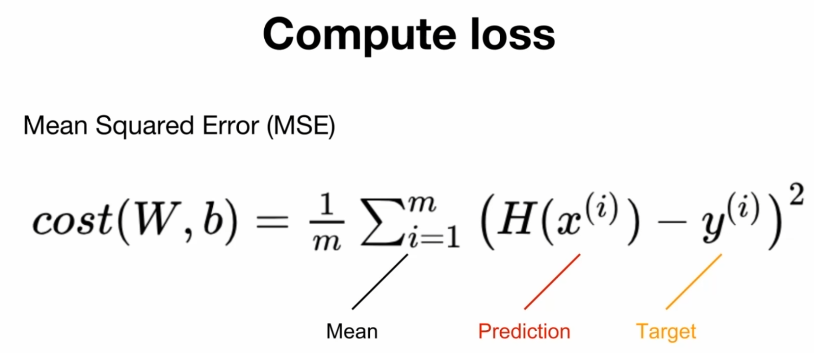
Pytorch를 통해 구현한다면,
torch.mean((hypothesis - y_train) ** 2)
# 직접 구현
torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')
# 내장 라이브러리처럼 사용할 수 있습니다.
Gradient Descent
loss function을 통해 loss를 구했다면, 그 loss를 줄이기 위해 모델을 개선해야 합니다. 가장 대표적인 방법이 Gradient Descent(경사하강법)입니다.
미분을 통해 loss function의 기울기를 계산해서 기울기가 0이 되는 방향으로 learning rate 만큼 weight와 bias를 이동시킵니다.
torch.optim 라이브러리를 사용하면, 모델 개선 optimizer를 이용할 수 있습니다. 가장 유명한 SGD를 사용해 보겠습니다.
hypothesis = x_train * W + b
cost = torch.mean((hypothesis - y_train) ** 2)
# 또는 cost = torch.nn.MSELoss()
optimizer = optim.SGD([W, b], lr=0.01)
optimizer.zero_grad() # gradient 초기화
cost.backward() # gradient 계산
optimizer.step() # 모델 개선정리
과정을 정리하면 다음과 같습니다.
1. 데이터 정의
2. Hypothesis 초기화
3. Optimizer 정의
4. Hypothesis 예측
5. Cost 계산
6. Optimizer로 학습
(4~6 반복)
