최소비용으로 모든 거리 돌기!

DKf·2023년 9월 20일

Algorithm

목록 보기

2/9

안녕하세요. 오늘은 모든 지역을 방문한다고 가정할 때, 최소비용이 얼마일까?라는 내용으로 포스팅을 준비해봤습니다. 프로그래머스에서 섬 건너기 문제에서 낭패를 맛봐 포스팅을 했씁니다! 사람들이 흔히 착각하는 알고리즘으로 최소비용과 최단거리인데요. 이 두가지는 엄연히 다릅니다.. 오늘은 크루스칼 알고리즘을 위주로 공부해봤습니다.

최단 거리 알고리즘 : 어떻게 하면 가장 빨리 갈 수 있는가? (다익스트라, A*알고리즘)

최소 비용 알고리즘 : 가장 적은 비용으로 모든 지역을 방문할 수 있을 까? (크루스칼, 프림 알고리즘)

🎓 사전지식

먼저 최소 비용 알고리즘 중 크루스칼 알고리즘을 이해하기 위해 신장트리와 서로소 집합 자료구조를 이해하고 계셔야 합니다.

신장트리(Spanning Tree)

신장트리는 두가지의 조건을 만족하는 트리 구조입니다.
1. 모든 노드가 연결되어 있다.
2. 사이클이 존재하지 않는다. (트리의 조건을 만족합니다.)

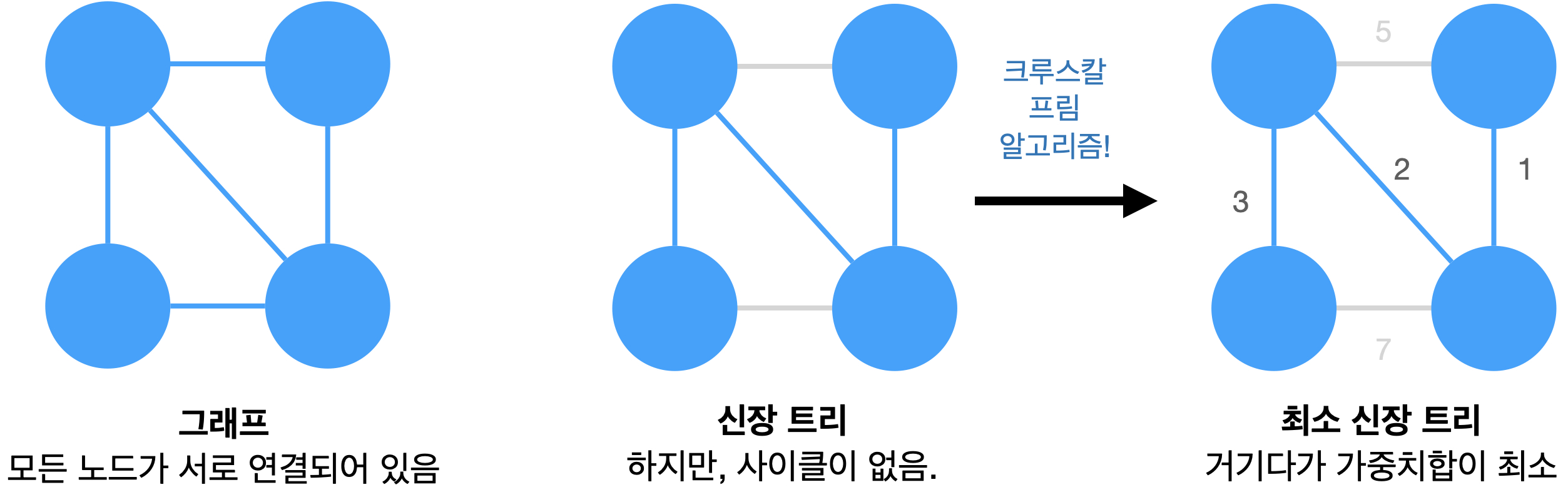
상위 그림을 보면, 간선의 가중치 합이 최소인 트리를 최소 신장 트리(Minimum Spanning Tree)라고 부릅니다.

서로소 집합 자료구조(Disjoint set)

서로소 집합 자료구조는 다음과 같이 공통 원소가 없는 두 집합을 의미합니다. 이 개념은 추후 그래프 알고리즘에서 용이하게 사용됩니다. 간선에 의해 사이클이 생기는지 안생기는지를 체크하는 알고리즘을 통해 노드를 찾거나 합칠 때 유용하게 사용됩니다.

서로소 집합 : {1, 2}, {3, 4}
서로소 집합이 아니다. : {1, 2}, {2, 3}

노드를 찾거나 합칠 때 유용하게 사용한다고 했는데 그럼, 어떻게 사용하는 걸까요? 주로 사이클을 판별할 때 사용합니다. 사이클을 판별해서 사이클이 돌지 않으면 최소 신장 트리임을 알 수 있죠. 또, 간선의 최소 비용도 확인할 수 있죠.

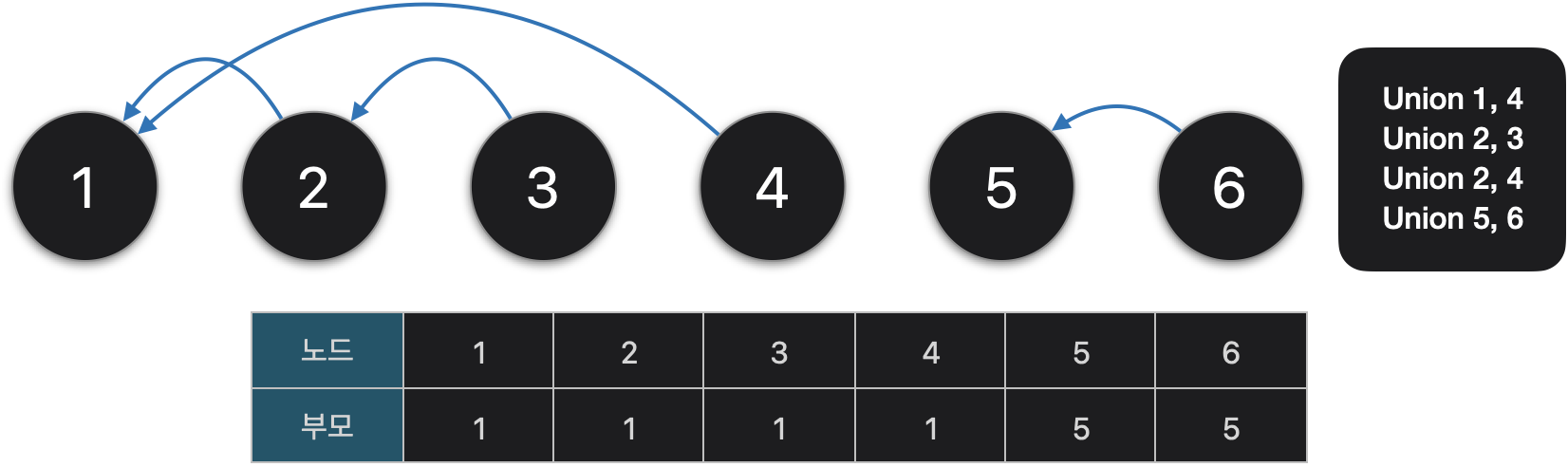
다음과 같은 노드들이 있다고 가정해봅시다. 2,3,4번 노드는 근본적으로 1번과 이어져있고 5,6번 끼리 이어져 있습니다. 우리는 이제 {1, 4}, {2, 3}, {2, 4}, {5, 6} 원소들이 서로 속한 집합인지 확인하고 합치는 작업을 진행합니다.

# 노드의 개수 : 6, 간선의 개수 : 4
# {1, 4}, {2, 3}, {2, 4}, {5, 6}

v, e = map(int, input().split()) # 노드, 간선
parent = [0] * (v+1) # 노드의 개수로 부모 테이블을 생성합니다.

# 부모 테이블에 노드 값을 자기 자신으로 초기화 합니다.
for i in range(1, v+1):
    parent[i] = i

def find_parent(parent, x):
    # 루트 노드가 아니라면, 루트노드를 찾을 때 까지 재귀 호출
    if parent[x] != x:
        return find_parent(parent, parent[x])
    return parent[x]


def union_parent(parent, a, b):
    # 두 원소가 속한 집합 합치기
    a = find_parent(parent, a)
    b = find_parent(parent, b)

    if a < b:
        parent[b] = a # 가장 적은 값 넣기
    else:
        parent[a] = b


for i in range(e):
    a, b = map(int, input().split())
    union_parent(parent, a, b)

그리고 사이클을 판별해보겠습니다.

cycle = False

for i in range(e):
    a, b = map(int, input().split())
    # 사이클이 발생할 경우 종료
    if find_parent(parent, a) == find_parent(parent, b):
       cycle = True
       break
    
    # 사이클이 발생하지 않은 경우 합집합 수행
    else : union_parent(parent, a, b)

path Compression(경로 압축)

Union-Find 알고리즘은 순서에 따라 최악의 경우 연결리스트와 같은 형태가 될 수 있습니다. 그래서 저는 좀 더 효율적인 시간 복잡도를 위해 거쳐간 노드를 루트에 다이렉트로 연결하는 방법을 사용했습니다. 이렇게 되면 $O(V)$ 에서 $O(V + M\log N) = O( M\log V)$ 으로 갖게 됩니다.

def find_parent(parent, x):
    # 루트 노드가 아니라면, 루트노드를 찾을 때 까지 재귀 호출
    if parent[x] != x:
        return find_parent(parent, parent[x])
    return parent[x] # 경로 압축

Union-By-Rank

이 방법은 크기가 작은 트리를 큰 트리의 루트(root)에 이어 붙이는 방법을 의미합니다. 이 방법을 사용하기 위해 각 트리마다 rank라는 배열으로 기억해두었다가 rank가 큰 트리에 합치게 됩니다.

# union by size
rank = [1 for _ in range(n)]
def union(a, b):
	a = find(a)
	b = find(b)
	
	if rank[a] < rank[b]:
		a, b = b, a # swap
	
	parent[b] = a
	rank[a] += rank[b]

# union by height
rank = [1 for _ in range(n)]
def union(a, b):
	a = find(a)
	b = find(b)

	# 한쪽이 큰 경우
	if rank[a] < rank[b]:
		a, b = b, a # swap
        # parent[a] = b
	else:
		parent[b] = a
    	# rank가 서로 같은 경우
		if rank[a] == rank[b]:
			rank[a] += 1

[참조] 서로소 집합(Disjoint Set) & 유니온 파인드(Union find) - yoongrammer

관련 문제 풀어보기 [백준] 10775 - 공항

📌 크루스칼 알고리즘

크루스칼 알고리즘은 가장 적은 비용으로 노드를 연결할 수 있는 알고리즘으로 그리디 알고리즘(Greedy)으로 분류됩니다.

💡크루스칼 알고리즘이 왜 탐욕 알고리즘인거죠?
우선, 탐욕 알고리즘은 현재의 상황에서 최적의 답을 찾는 알고리즘입니다. 크루스칼 알고리즘도 마찬가지로 사이클이 존재하지 않은 상황에서 최소 비용이 되는 답을 반복하여 최적의 해를 구하기 때문에 탐욕 알고리즘으로 분류되는 것입니다.

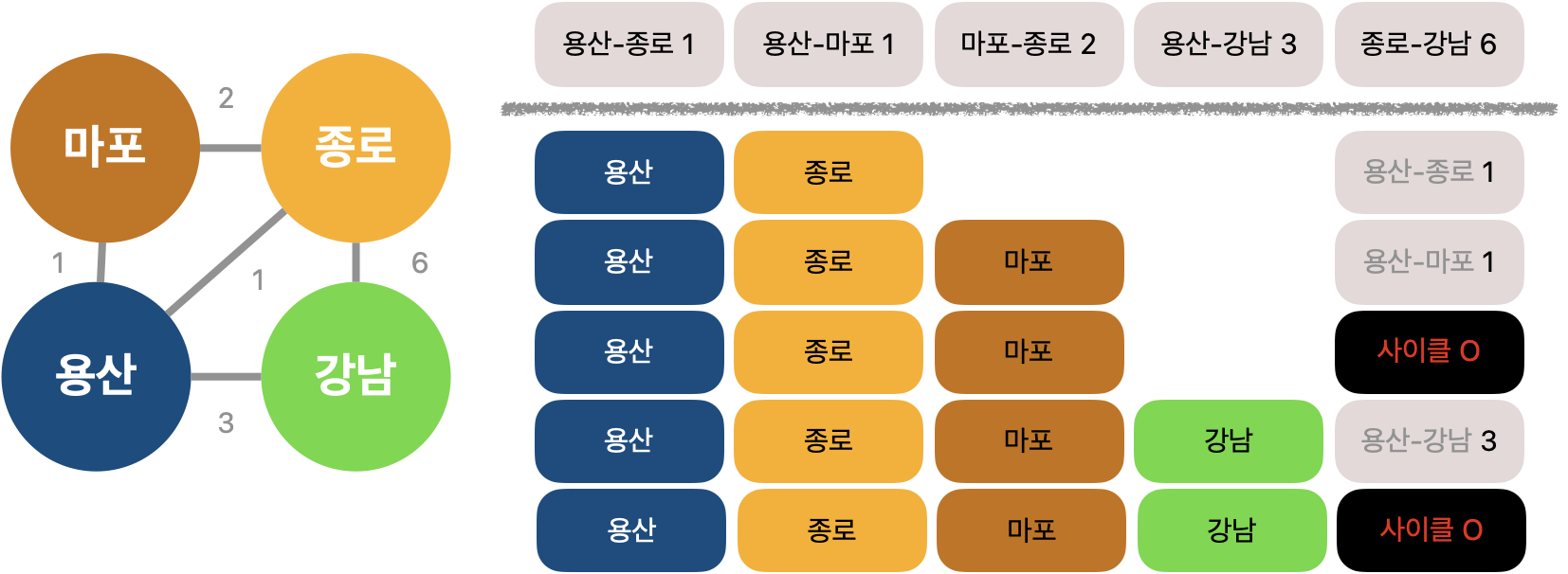
우선 간선을 정렬한 다음, 비용이 가장 적은 간선 부터 집합에 포함시킵니다.

이 때, 사이클이 발생하는 간선은 집합에 포함하지 않습니다.


최종비용 = 0
부모테이블 = [노드만큼]
  
간선들.sort(key=비용)

간선을 하나씩 확인하여 사이클이 발생하는지 확인합니다.

사이클이 발생하지 않은 경우에만 집합에 포함합니다.

for 간선 in 간선들:
    노드 a == 노드 b?
    합치기(a, b)
    최종비용 += 간선

이때 노드들은 부모 테이블의 부모 노드여야 합니다.

🏄‍♂️ 문제

팀 결성 문제 풀어보기

난이도 : ⭐️⭐️
풀이시간 : 20분
제한 시간 : 2초

학교에서 학생들이 0번부터 N번까지 번호를 부여했습니다. 처음에는 모든 학생이 서로 다른 팀을 구분되어 N+1개의 팀이 존재합니다. 이때 선생님이 '팀 합치기'와 '같은 팀 여부 확인' 연산을 사용할 수 있습니다.

팀 합치기 연산으로 두 팀을 합치는 연산입니다. 0 a b 형태로 주어집니다.
같은 팀 여부 확인 연산으로 1 a b 연산으로 같은 팀이 속해 있는지 확인합니다.

선생님이 M개의 연산을 수행할 때, '같은 팀 여부 확인'에 대한 연산 결과를 출력하세요.

입력예시

7 8 # N, M
0 1 3 # 연산, a, b
1 1 7
0 7 6
1 7 1
0 3 7
0 4 2
0 1 1
1 1 1

풀이

우선, 인원과 연산을 입력 받고 Union-Find 문제를 풀기 위해 인원 별 부모 테이블을 만들어 부모 값이 동일하면 같은 팀이고 동일하지 않으면 다른 팀임입니다.

N, M = map(int, input().split()
parent = [0] * (N+1)

for i in range(0, N+1):
    parent[i] = i

이제 선생님의 연산을 받아 0인 경우는 팀합치기, 1인 경우는 같은 팀 여부를 확인해 같은 팀이면 YES를 출력합니다.

def find_team(parent, x):
    if parent[x] != x:
        parent[x] = find_team(parent, parent[x])
    return parent[x]


def union_team(parent, a, b):
    a = find_team(parent, a)
    b = find_team(parent, b)
    if a < b:
        parent[b] = a
    else:
        parent[a] = b
        
for i in range(M):
    operation, a, b = map(int, input().split())
    if operation == 0:
        union_team(parent, a, b)
    elif operation == 1:
        if find_team(parent, a) == find_team(parent, b):
            print('YES')
        else:
            print('NO')

섬 연결하기

N개의 섬 사이에 다리를 건설하는 비용(costs)가 주어질 때, 최소의 비용으로 모든 섬이 통행 가능하도록 마들 때 필요한 최소 비용을 return 하시오.

다리를 여러번 건너더라도, 도달할 수 있으면 통행 가능합니다.

섬의 개수 n은 1이상 100이하입니다
costs의 길이는 ((n-1)*n / 2)입니다.
같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
연결할 수 없는 섬은 주어지지 않습니다.

n	costs	return
4	[[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]]	4

[프로그래머스] 42861 - 섬 연결하기

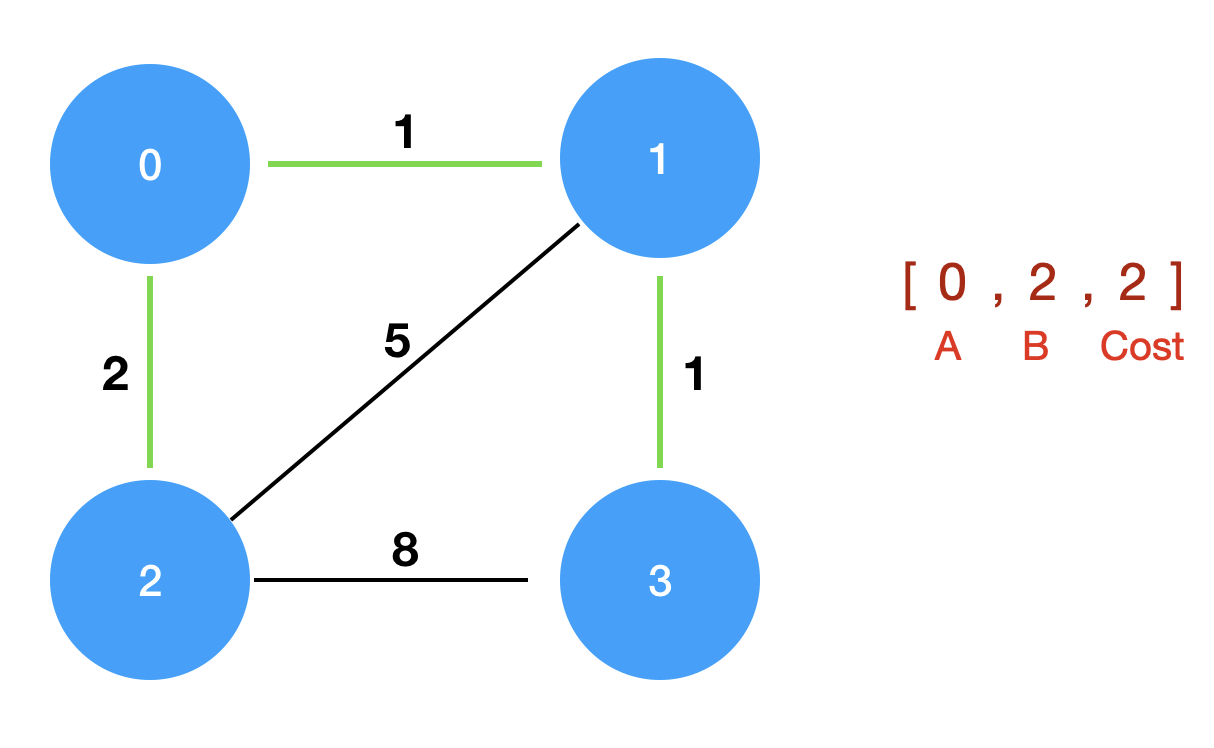
풀이

먼저 간선을 비용 기준으로 오름차순 합니다.

costs.sort(key = lambda x : x[2])
# [[0, 1, 1], [1, 3, 1], [0, 2, 2], [1, 2, 5], [2, 3, 8]]

낮은 가중치의 간선 부터 사이클이 형성하는 간선이라면 제외(continue)하고 그렇지 않으면 connect(연결되는 집합)에 추가합니다.

즉 중복이되는 경우를 방지하기 위해 set 자료구조를 사용했으며 반복문을 돌면서 크루스칼 알고리즘을 이용해 최소비용을 구합니다.

connect = set([costs[0][0]) # 연결이 확인되는 집합
# {0}

    while len(connect) != n:
        for cost in costs:
            # 사이클이 허용되는 노드들인 경우
            if cost[0] in connect and cost[1] in connect:
                continue
            # 사이클이 허용되지 않은 노드들인 경우
            if cost[0] in connect or cost[1] in connect:
                connect.update([cost[0], cost[1]])
                answer += cost[2] # answer에 비용 추가
                break
     return answer