안녕하세요. 오늘은 해시테이블에 대한 개념을 정리해보려고 합니다.
해시(Hash)?
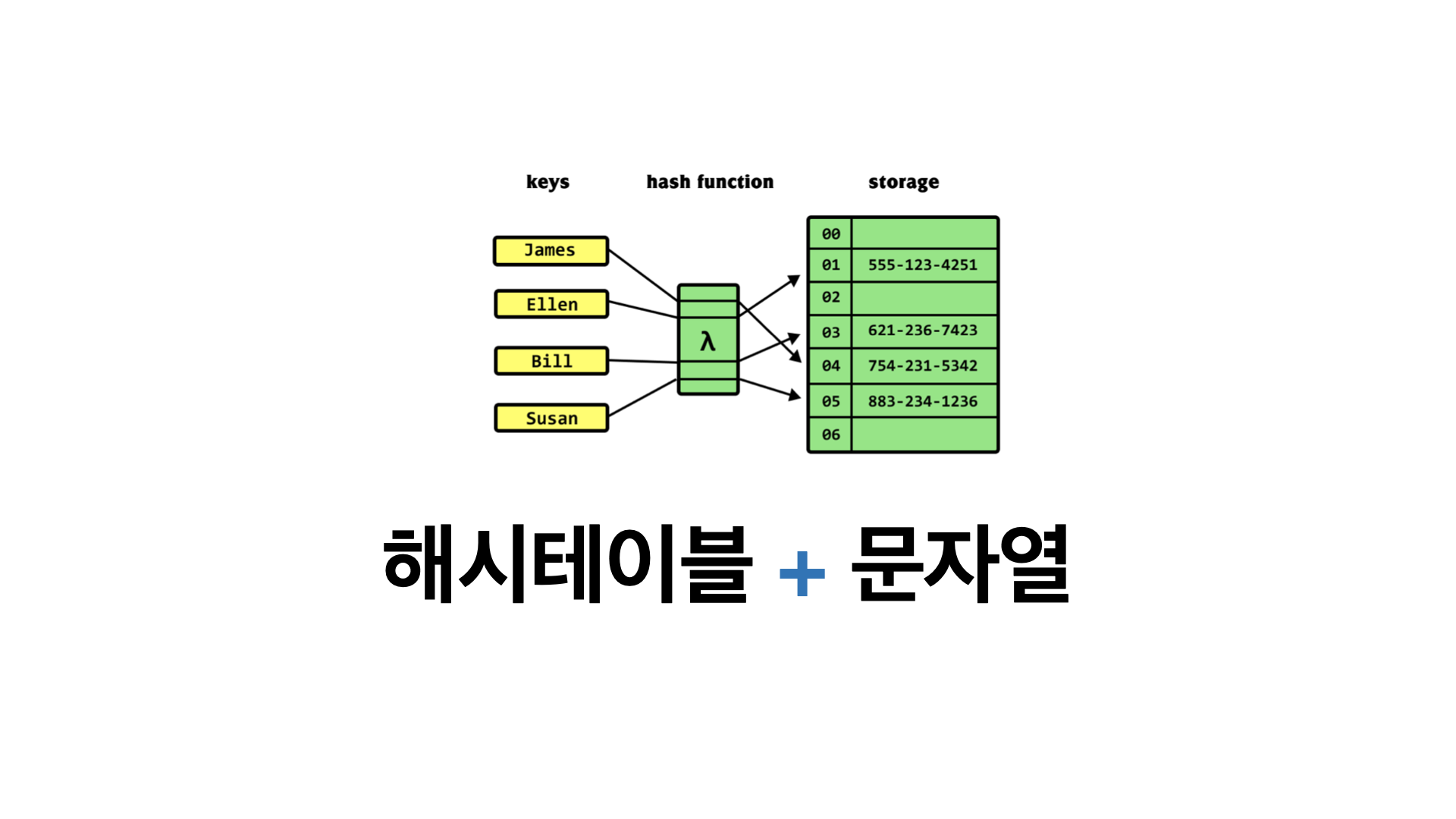
해시 구조는 키(key)로 접근하여 값(Value)를 반환하는 데이터 구조를 의미합니다. 여기서 해시(Hash)의 의미는 해시함수에 key를 대입하여 나온 결과 값을 의미합니다. 그렇다면 해시 함수는 무엇일까요? 해시함수는 키를 값으로 변환해주는 알고리즘을 의미합니다.
해시 구조는 왜 필요한가요?
만약에 배열(array)을 통해 데이터를 찾아낸다면 인덱스(index)를 통해 찾으실 수 있을 것입니다.
그런데 만약 인덱스의 크기가 크다면 어떻게 될까요? 해당 인덱스를 찾기위한 시간이나 배열 메모리 비용도 증가하게 될 것입니다.
해시구조는 이러한 단점을 보완할 수 있는 장점을 가지고 있습니다. 임의의 크기를 가진 인덱스를 고정된 크기로 매핑할 수 있죠. 그리고 키를 통해 바로 값을 찾을 수 있다보니 데이터를 찾기 위해선 해시 구조는 일반적으로 의 시간 복잡도를 가집니다.
분할 상환 방식의 복잡도 : 원소 삽입보다 읽기가 더 많이 쓰이기 때문에 시간을 상쇄합니다.
해시 구조는 저장 및 검색 속도가 빠릅니다. 그러나 저장공간(버킷) 또한 데이터 공간 만큼 필요합니다.
해시 구조는 주로 어디에 사용되나요?
해시 구조는 검색이나 조회에 빠른 속도를 내다보니 검색이 많이 필요한 경우나 캐시를 구현해야하는 경우 중복을 확인하기 위해 사용합니다. 또다른 예로, 해당 그래프가 사이클이 발생하는지 확인하기 위해 DFS나 BFS를 사용하는 것보다 모든 자원에 고유번호를 등록하여 고유 번호와 동일한 값이 존재한다면 사이클이 발생하는 것으로 확인할 수 있습니다.
해싱(Hashing)과 해시 테이블(Hash Table)
해싱은 해시함수를 통해 임의의 길이(key)를 고정된 크기의 값(Hash)으로 변환하는 작업을 말합니다. 해싱은 이진탐색트리나 배열에 비해 훨씬 빠른 속도로 데이터를 탐색하거나 삽입, 삭제 할 수 있습니다. 이렇게 변환된 데이터를 저장하는 자료구조가 해시 테이블인 것입니다.
해시 테이블이 있기전에 아주 간단한 테이블이 있습니다.
Direct Address Table
이름 그대로 키 값을 주소로 사용하는 테이블을 말합니다. 키(key)가 17이면 17이라는 인덱스에 데이터를 저장하는 것을 말합니다. 이러한 경우에는 최대 키를 알고 있어야 할 뿐더러 키값이 골고루 분포가 되어 있지 않으면 메모리 낭비가 발생할 수 밖에 없습니다.
Hash Table
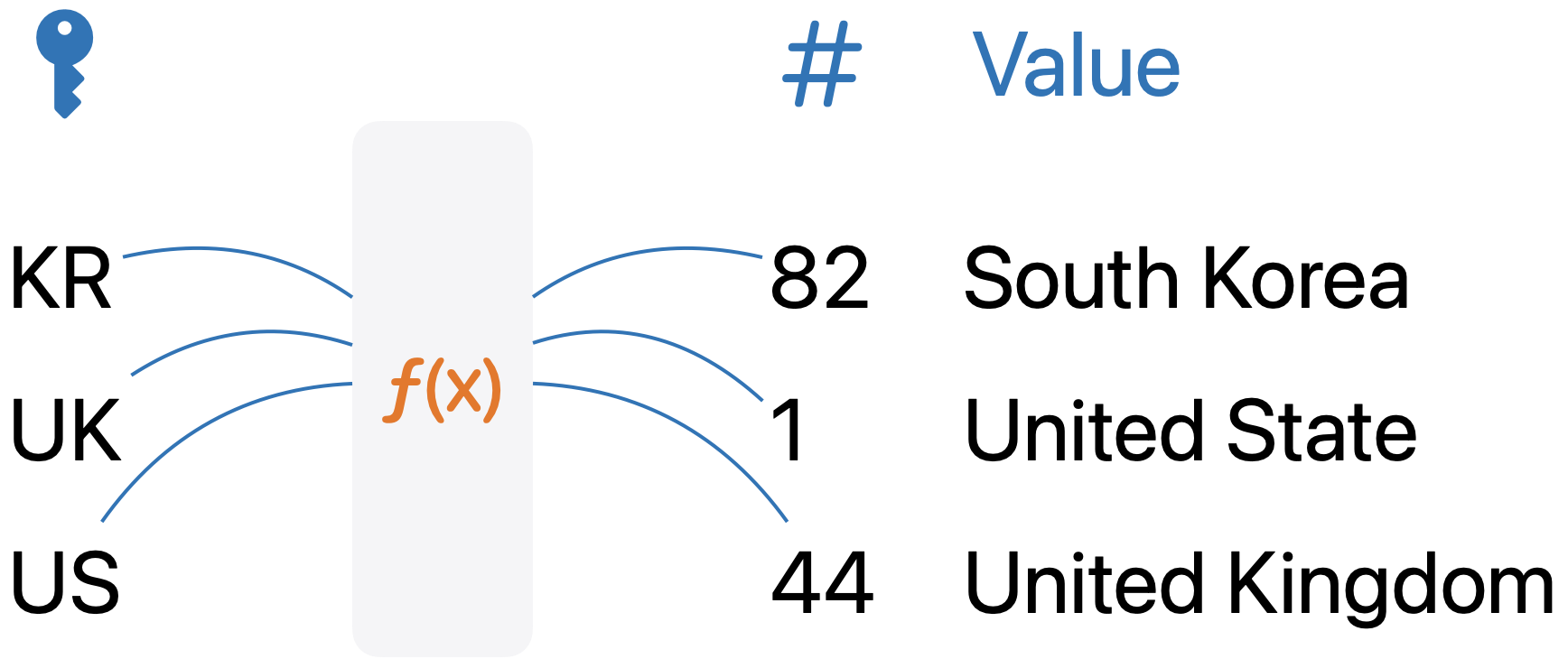
이번엔 해시함수를 사용해 해시값을 인덱스로 변환해 키 값과 데이터를 저장하는 자료구조입니다. 위 그림에서 해시(#)와 값(Value)사이에 인덱스를 통해 접근하는 구조를 말합니다.
class HashTable:
def __init__(self):
# 해시 테이블의 공간 : 100
self.table_length = 100
self.hash_table = list([None for i in range(self.table_length)])
def hash_function(self, key):
# 해시 함수 : 문자열의 철자마다 숫자로 만들어 합을 구합니다. 그 다음 테이블 길이와 나눕니다.
ord_sum = 0
for letter in key:
ord_sum += ord(letter)
return ord_sum % self.table_length
def insert(self, key, value):
# hash_value(=key) , value
self.hash_table[self.hash_function(key)] = value
def read(self, key):
# key 값을 이용해 값 반환
return self.hash_table[self.hash_function(key)]
def print(self):
for idx, value in enumerate(self.hash_table):
if value: # is not None
print(idx, value)
ex_table = HashTable()
ex_table.insert('Kang', 7459)
ex_table.insert('Kim', 8345)
ex_table.insert('Lee', 7500) # Idi 와 동일한 해시값을 가짐
ex_table.insert('Idi', 4523) # 해결을 위해 넓은 범위의 숫자를 생성할 수 있도록 수정이 필요함.
print(ex_table.read('Kang'))
ex_table.print()
Hash Function(해시 함수)
해시 함수는 임의의 길이 데이터를 고정된 길이의 데이터로 매핑하는 함수를 의미합니다. 대표적인 해시 함수 알고리즘으로 SHA-1, SHA-256, Dictionary등이 있습니다.
나눗셈을 이용한 해싱 방식
가장 기본적인 해시함수입니다.
num = [123, 45, 392, 45]
a = list
for i in nums:
a.append(i%7)
인코딩을 이용한 해싱 방식
str객체를 byte 객체로 변환하는 방법입니다.
to_byte = "hello".encode() # 문자열을 인코딩 -> byte
sum = 0
for byte in to_byte:
sum += byte # 문자 하나하나 바이트 씩 더함
print(sum) # 최종 byte의 합해시라이브러리를 이용한 해싱 방식
앞서 소개한 sha256을 사용한 방식으로 블록 암호화 기법으로 사용되는 방법입니다.
import hashlib
data = 'seoul1!'.encode() # 문자열을 이진코드로 변경
hash_object = hashlib.sha1() # 해시 객체 생성
hash_object.update(data) # 유니코드 해시 암호화
hex_dig = hash_object.hexdigest() # 6진수 숫자를 두배의 길이를 가진 문자열 객체로 반환
'''
딕셔너리
- a[3] = [1, 2, 3] # 변수에 리스트 대입
- a.keys() # 딕셔너리 뷰 객체 반환
- a.items() # 딕셔너리 뷰 객체 반환
- a.get(key) # 키로 값 얻기
- a.clear() # 초.기.화
'''💡 딕서너리의
get()함수
딕셔너리에서는 유용한데 잘 사용하고 있지 않았던 함수입니다.사람마다 다르겠지만 저는 이 함수를 잘 사용하지 않았기 때문에 문제 풀 때 제대로 접근을 못했었다는,,,get 함수는 키에 대한 value 값을 반환하는데 보통get(key, default=None)으로 이루어져 있기 때문에 키가 존재하지 않으면 에러를 발생하지 않고None을 리턴하게 됩니다. 그렇다면if a.get('nonekey')로 사용할 수 있겠죠.
해시 충돌이 발생하게 된다면?
만약에 앞앞 코드인 Lee와 Idi는 동일한 해시값을 갖습니다. 이러한 경우 해시 충돌(Hash Collision)이 발생하게 됩니다. 물론 이러한 경우 제산법(Division)이나 제곱법(Mid-Square), 폴딩법(XOR Folding), 숫자 분석법, 호너의 룰등 다양한 방법으로 교체하여 해시 메모리를 넓힐 수 있습니다. 그러나, 아무리 해시 함수를 잘 작성한다 한들 완벽하게 충돌은 피할 수 없습니다. 그래서 충돌을 처리하는 방법이 필요합니다.
충돌을 해결하는 대표적인 방법
- 오픈 해싱
- 체이닝 방법(Chaining)
- 클로즈 해싱
- 탐사 방법(Open Addressing, Probing) : 선형 탐색, 이차 탐색
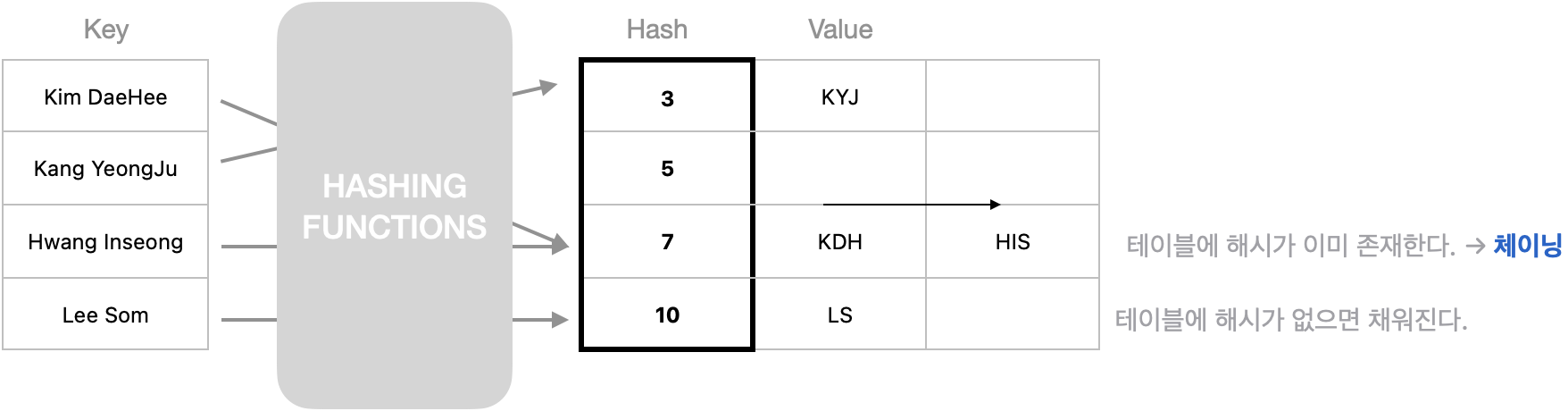
체이닝
오픈 해싱 기법 중 가장 대표적인 방법입니다. 해시 충돌이 발생한 경우 연결리스트 또는 이중 리스트를 이용해 연이어 데이터를 추가하는 방법입니다. 체이닝의 단점으로 한다면, 데이터가 많을 수록 메모리도 그만큼 낭비가 될 수 있다는 것입니다.
def chain_hash(hash_table, key, value):
h_key = hash(key) # 키(key)로 해시 함수를 거쳐 해시 값을 받습니다.
hash_table[h_key].append(value) # 해시 값 위치에 value를 연이어 넣습니다.
return hash_table
간단히 이중 리스트로 구현할 수 있지만 연결 리스트로 구현하면 복잡하지만 더 빠른 성능을 낼 수 있습니다.
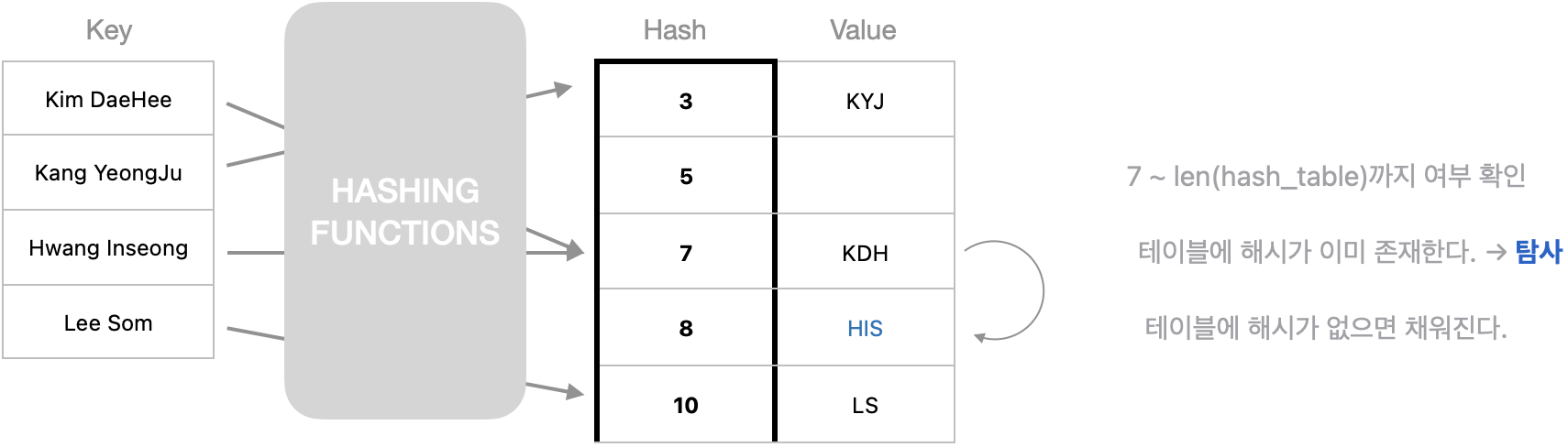
탐사
충돌이 발생하면 다음 요소가 비어있는지 확인하고 비어있는 경우 저장하는 방식입니다. 충돌이 발생하면 다음 다음 다음 다음을 찾다보니 군집화가 발생하는 단점이 있습니다.
def prob_hash(hash_table, key, value):
h_key = hash(key) # 키(key)로 해시 함수를 거쳐 해시 값을 받습니다.
# Load Factor #
while True:
# 해시 테이블에 있는 슬롯에 값이 이미 존재하는 경우
if len(hash_table[h_key]) == 1:
h_key+=1 # 인덱스를 올리고 다시 while로 돌아간다.
if h_key == len(hash_table):
h_key = 0 # 만약 마지막 자리라면 앞으로(0) 돌아간다.
# 해시 테이블에 있는 슬롯에 값이 존재하지 않는 경우
else:
hash_table[h_key].append(value) # 비어있으면 바로 넣어준다.
return hash_table이차 탐사의 경우 탐사 순서에 단계를 이차식을 이용하여 결정합니다.
이러한 어드레싱 방법은 테이블에 저장되는 데이터가 고르게 분포하지 않아 뭉친다는 단점이 존재합니다. 이를 군집화(Clustering)이라고 하는데요. 이러한 클러스터들이 점점 커지게 되면 다른 클러스터와 합치게 되어 특정 위치에 데이터가 몰리게 되는 현상이 일어납니다. 특정 구간에 몰리게 되니 탐색하는 시간도 오래 걸리기 때문에 해싱의 효율성도 낮아지게 됩니다. 이러한 키들을 잘 분산시키기 위해 도와주는 것이 로드팩터(Load Factor) 라고 합니다.
로드 팩터는 해시테이블에 저장된 데이터 개수 N을 버킷 개수 K로 나눈 것과 동일합니다. 로드 팩터가 증가할수록 테이블의 성능은 감소하게 됩니다. 대표적인 예로 비둘기집 원리가 있습니다. 비둘기가 셋인데 집이 둘이면 두 비둘기는 충돌이 일어날 수 밖에 없고 이는 성능을 감소시키게 됩니다. 보통 75% 정도 공간이 차있으면 새로운 테이블을 생성해줍니다.

# LOAD FACTOR
# 만약 테이블 사용 공간이 75%를 넘으면,
if len(hash_tavle) - hash_table.count([]) >= int(len(hash_table)*0.75):
hash_table.extend([[] for _ in range(int(len(hash_table)*0.5))]) # 공간 확대
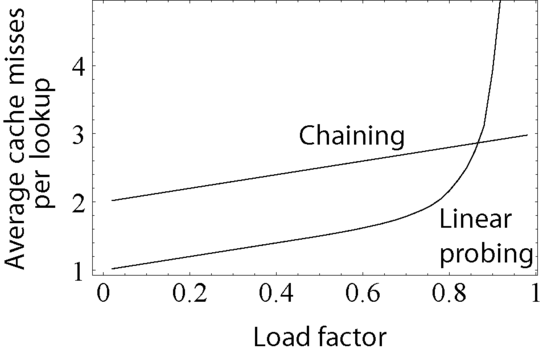
파이썬에서는 두가지 충돌 해결 방법 중에서 오픈 어드레싱을 사용하는 편입니다. 그 이유는 일반적으로 체이닝을 사용하는 연결리스트보다 딕셔너리를 사용하는 것이 더 메모리 할당을 필요하지 않기 때문입니다. 오픈 어드레싱 방법이 체이닝보다 성능이 더 좋습니다. 그러나 80%이상 슬롯을 사용하게 되면 성능 저하가 일어나 로드팩터를 줄여 성능을 저하하는 게 좋습니다.
문제) 베스트 앨범
import pandas as pd
def solution(genres, plays):
answer = []
# 장르별 트랙과 재생수를 담은 딕셔너리
dict1 = {}
# 장르별 재생 수 합계를 담은 딕셔너리
sum_dict = {}
# 데이터화
for idx, (genre, play) in enumerate(zip(genres, plays)):
if genre not in dict1:
dict1[genre] = [(idx, play)]
else:
dict1[genre].append((idx, play))
if genre not in sum_dict:
sum_dict[genre] = play
else:
sum_dict[genre] += play
# 합계 순서대로 정렬 -> 정렬된 순서대로 인덱스와 재생수를 꺼내 최대 2개까지(:2) answer에 넣음
for (k, v) in sorted(sum_dict.items(), key=lambda x:-x[1]):
for (i, p) in sorted(dict1[k], key=lambda x:-x[1])[:2]:
answer.append(i)
print(sorted(dict1['classic'], key=lambda x:-x[1])[:2])
return answer