안녕하세요. 오늘은 완전 탐색에 대해 배워보고 실제로 이를 효율적으로 해결하기 위한 이분탐색에 대해서도 알아봅시다.

완전탐색과 브루트 포스?

완전 탐색(Exhaustive Search)은 가능한 모든 경우의 수를 탐색하여 최적의 결과를 찾는 방법을 의미합니다. 모든 경우의 수를 탐색하기 때문에 최적의 해를 찾을 수 있다는 정확성은 보장하지만 그만큼, 시간과 메모리 소모도 크기 때문에 시간 복잡도가 $O(N)$ 혹은 $O(N^2)$이 될 수 있습니다.

💡 경우의 수
경우의 수는 한번의 시행에서 일어날 수 있는 사건의 가지 수를 의미합니다. 주사위 던지기의 경우 경우의 수는 {1, 2, 3, 4, 5, 6} 중 하나인 셈이죠. (6가지)

그렇다면, 브루트포스(Brute Force)는 무엇을 의미할까요?
브루트 포스는 우리가 알고 있는 완전탐색이랑 동일한 것 아니냐 생각하실 것입니다. 하지만 브루트 포스는 완전탐색을 이용해 결과를 도출하는 알고리즘으로 목적이 다릅니다. 그렇다면, 브루트 포스 알고리즘 말고도 어떤 알고리즘이 있는지 완전 탐색 알고리즘에 대해 자세히 알아봅시다. 완전 탐색 알고리즘의 종류로는 다음과 같습니다.

• 브루트 포스(Brute Force) $O(nm)$
• 비트 마스크(Bit Mask): $O(2^n * n)$
• 백 트래킹(Back Tracking): $O(n!)$, 비선형 구조
• 순열(Permutation) $O(n!)$
• 재귀 함수(Recursion) $O(n)$
• DFS, BFS: $O(V+E)$, 비선형 구조

이 알고리즘들은 모두 경우의 수에 따라 결과를 도출시킨다는 공통점이 존재합니다.

브루트 포스(Brute Force)

브루트 포스 알고리즘은 앞에 명시한 대로 완전탐색을 이용한 알고리즘입니다. 정확성 100%의 예상된 결과를 도출하지만 그만큼 경우의 수가 많을 수록 시간이 오래걸린다는 단점이 존재합니다.

주로 반복문이나 재귀 함수를 이용해 문제를 해결하곤 합니다. 만약에 다음과 같이 holland loves new iPhone Pro 15 라는 문자열에서 i라는 철자를 찾는다고 가정했을 때 어떻게 찾을 수 있을까요? 간단히 반복문을 작성하면 됩니다. 물론, $O(N)$이라는 시간 복잡도를 갖겠죠.

def sequentialSearch(string, value):
    for i in range(len(string)):
        if string[i] == value: # 해당 원소가 값이랑 같은 경우
            return i
    return False

x = 'holland loves new iPhone Pro 15'
value = 'i'

print(sequentialSearch(x, value))

만약에 i가 아니라 new라는 문자열이라면 어떻게 구현해야할까요?
다음과 같이 투포인터(Two-Pointer)기법으로 구현할 수 있습니다.

def sequentialSearch(string, value):
    string_pointer = 0
    value_pointer = 0
    # 만약 value 포인터를 다채웠거나 string 포인터를 다채우게 되면 리턴
    while string_pointer != len(string) and value_pointer != len(value):
        # 철자가 맞는 경우 두 포인터를 +1
        if string[string_pointer] == value[value_pointer]:
            string_pointer += 1
            value_pointer += 1
        else:
            # 철자가 틀린 경우 두번째 문자열 부터 다시시작, value 초기화
            string_pointer = string_pointer - value_pointer + 1
            value_pointer = 0
    # 만약 value 포인터가 다 맞는 경우 
    return string_pointer - value_pointer if value_pointer == len(value) else None


x = 'Holland loves new iPhone Pro 15'
value = 'Pro'

print(sequentialSearch(x, value))

💡 투 포인터 기법(Two Pointer)
투 포인터 기법은 다음과 같이 문자열 검색 뿐만아니라 특정합을 가지는 연속된 수열을 찾거나 정렬된 두 리스트의 결과를 낼 때도 사용합니다.

재귀 함수(Recursion)

반복문을 통해 최선의 답을 도출하는 브루트 포스(Brute Force) 방법 뿐만아니라 자기 자신을 호출하여 모든 가능한 경우의 수를 체크하면서 최적의 해답을 얻는 방식인 재귀 함수(Recursion)도 존재합니다.
재귀함수는 반복문을 사용하는 것보다 코드가 간결하지만, 스택 범위가 제한되어 있어 오버플로우가 발생할 수 있다는 단점이 존재합니다.

n = 5

# 반복
num = 5
for i in range(n):
    num +=i
print(num)

# 재귀
def sums(n):
    # 종료 조건(Base Case) 필수
    if n ==1:
        return 1
    return n + sums(n - 1)
print(sums(n))

대표적으로, 재귀 함수하면 피보나치 수열 또는 하노이탑 문제가 있습니다.

'하노이의 탑'은 (Tower of Hanoi) 프랑스의 수학자 에두아르 뤼카가 1883년 소개한 문제이다. '작은 원반 위에 큰 원반을 올릴 수 없다'는 규칙을 가지고 있는데, 알고리즘으로는 재귀함수의 좋은 예제가 된다.

다음과 같이 A,B,C의 하노이 탑이 존재 할 때, A탑에 있는 원판 n개를 C탑으로 옮기려고 합니다. 이럴 때, A번에서 C번으로 옮기는 최소 횟수를 구하시오.

def solution(n):
    answer = []
    def hanoi(start, target, inter, n): # 인자 순서 넣어주는 게 좀 헷갈렸음.
        if n == 1:
            answer.append([start, target])
        else:
            # 원판 N-1을 A에서 B로 이동
            hanoi(start,inter,target,n-1)
            # 제일 밑에 있는 원판을 C로 이동
            hanoi(start,target,inter,1)
            # B에 있는 원판을 목적지 C로 이동
            hanoi(inter,target,start,n-1)
            
    hanoi(1,3,2,n)
    
    return answer

하노의 탑 문제 - 프로그래머스 →

백 트래킹

백 트래킹(Back Tracking)은 가능한 경우의 수를 탐색하는 과정(promising) 중 막히게 되는 경우 다시 돌아가 다른 경로를 탐색(pruning)하는 알고리즘입니다.

• 경우의 수를 줄일 수 있지만 재귀 함수를 사용하기 때문에 스택 오버플로우가 발생할 수도 있습니다.
• BFS는 인접 노드들을 큐에 넣고 뽑아내는데 큐에 크기가 증가하기 때문에 DFS로 하는게 더 좋은 방법입니다.

대표적인 예제로 홀짝만들기 3x3 행렬, N-Queen등이 문제들이 대표적입니다.
그 중에서 그나마 난이도가 낮은 홀짝 만들기 예제입니다.

A,B,C 세사람이 각자 가지고 있는 숫자들을 하나씩 줄 세운다고 가정했을 때, 짝수나 홀수가 연속으로 나오면 안되는 조건입니다. 이때, 만들 수 있는 숫자를 모두 구하면 됩니다. (순서는 A-B-C)

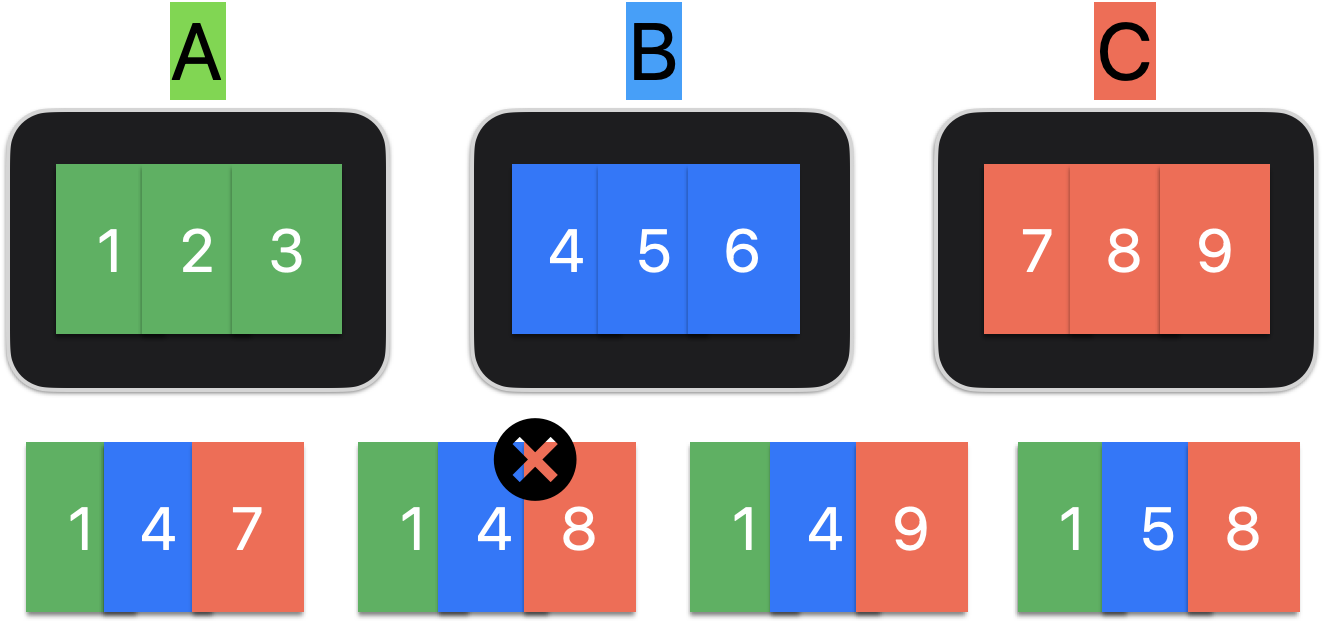
numbers = [[1,2,3],[4,5,6],[7,8,9]] # ABC 숫자를 차례대로 담은 2차원 배열

def solution(numbers):
    answer = []
    return dfs(numbers, 0, answer, [])
    # numbers
    # depth(현재 깊이):0
    # answer
    # history(depth까지의 숫자)

print(solution(numbers))
# [[1, 4, 7], [1, 4, 9], [1, 6, 7], [1, 6, 9], [2, 5, 8], [3, 4, 7], [3, 4, 9], [3, 6, 7], [3, 6, 9]]

백 트래킹에는 두가지 방법을 사용합니다.

• Promising(조건 체크) : 짝수나 홀수가 연속으로 나오면 안된다.
• Pruninig(가지치기) : 조건에 만족하지 않은 경우 돌아간다.

1. 만약 모든 숫자를 다 돌았을 경우(즉, A→B→C)

만약 depth 가 numbers 의 끝까지 도달했을 경우(즉, A→B→C)까지 도달했을 경우, 이 경우에는 숫자가 모두 조건에 맞다는 의미으므로 history 를 answer에 넣어줍니다. 그리고 다시 반복을 진행합니다.

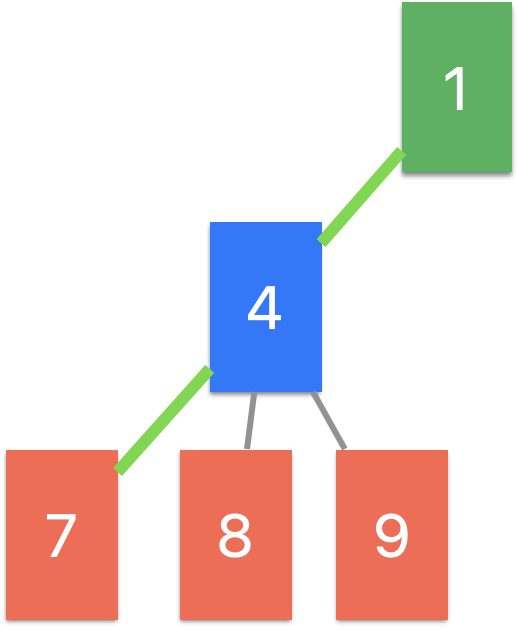
def dfs(numbers, depth, answer, history):
    # 깊이가 len(number)가 되면 수를 다 채웠기 때문에 정답을 반환합니다.
    if depth == len(numbers):
        answer.append(history[:])
        return

2. history 가 비어있는 경우(” ”→ A)

만약 가장 첫번째 숫자를 history 안에 넣어야 할 경우 숫자를 넣어주고 depth 를 +1 추가해줍니다.

if not history:
        # 
        for n in numbers[depth]:
            new_history = history[:]
            new_history.append(n)
            dfs(numbers, depth + 1, answer, new_history)

3. history가 비어있지 않은 경우(A→B or B→C)

만약 history 가 비어있지 않는다면(두번째로 추가해야하는 경우부터를 의미), 맨 마지막에 넣은 숫자와 현재 숫자를 비교해 연속되지 않는다면 history에 넣고 depth을 추가해줍니다.
해당 수가 일치하지 않는다면 dfs 재귀 함수를 돌지 않고 회귀할 것입니다. 이런식으로 반복하고 모든 수를 다돌게 되면 history 는 answer에 담길 것입니다.

else:
        for n in numbers[depth]:
            # 마지막 숫자가 짝수 이고 N이 홀수의 경우
            if history[-1] % 2 == 0 and n % 2 != 0:
                new_history = history[:]
                new_history.append(n)
                dfs(numbers, depth + 1, answer, new_history)

            # 마지막 숫자가 홀수 이고 N이 짝수의 경우
            if history[-1] % 2 != 0 and n % 2 == 0:
                new_history = history[:]
                new_history.append(n)
                dfs(numbers, depth + 1, answer, new_history)

결론적으로 백트래킹 문제는 상태 공간트리에서 제약조건에 만족(CSP)한 경우에 해를 찾는 문제이기 때문에 조건에 만족할 수록 깊이를 추가하는 것과 모든 조건을 만족했을 때 재귀함수를 마치는 조건이 중요한 것 같습니다.

💡 비트마스킹과 DFS, BFS는 포스팅할 내용이 길어 따로 포스팅할 예정입니다.

이분 탐색

정렬된 데이터를 대상으로 중앙 값을 이용해 검색하는 알고리즘입니다. 만약 데이터의 개수가 1,000만개를 넘게 되면 탐색 시간의 효율성을 위해 이진 탐색을 사용해야 합니다. 이럴 때 input() 함수로 입력하는 것보다 readline() 함수를 사용하면 시간 초과를 피할 수 있습니다.

• 시간 복잡도는 퀵 정렬과 비슷하게 절반씩 데이터가 줄어들기 때문에 $O(\log N)$입니다.
• 인덱스를 통해 중앙 값을 구할 때 소수점을 버립니다.

장단점

• 장점 : 탐색 조건이 적어 단순하다.
• 단점 : 데이터 양이 많은 경우 단순 반복을 해야하니 시간과 메모리가 많이 소비한다.

def binarySearch(array, target, start, end):
    while start <= end:
        # 1. 전체 데이터에서 중앙값을 선택합니다.
        mid = (start + end) // 2
        
        # 2. 중앙값과 찾고자 하는 값을 비교합니다.
        if array[mid] == target:
           return mid
        # 3-a. 중앙 값이 찾고자 하는 값보다 크다면 왼쪽 부분의 중앙 값을 취합니다.
        elif array[mid] > target:
             end = mid - 1
        # 3-b. 중앙 값이 찾고자 하는 값보다 작다면 오른쪽 부분의 중앙 값을 취합니다.
        else:
             start = mid + 1
     return None

• 재귀를 이용한 경우

# 재귀함수로 구현한 경우
def binary_search_recursion(array, target, start, end):
    # 정렬이 되어있지 않은 경우
    if start > end:
        return None 
    
    mid = (start + end) // 2 # 중간점 반환
    
    # 찾고자 하는 데이터가 중간값, 중간 초과, 중간 미만 일 경우
    if array[mid] == target: 
        return mid
    elif array[mid] > target:
        return binary_search_recursion(array, target, start, mid-1)
    else:
        return binary_search_recursion(array, target, mid + 1, end)

그외 탐색 알고리즘

KMP 검색

문자열 안에서 부분 문자열을 검색할 때, 실패한 위치를 기반으로 필요 없는 문자열을 건너뛰고 다음 번 검색 위치를 결정하는 알고리즘입니다.

BM 검색

검색할 문자열의 끝에서 부터 비교하다가 일치하지 않은 문자를 만나면 검색할 문자열 만큼 이동해 검색을 수행하는 알고리즘입니다.

참고

https://adjh54.tistory.com/197