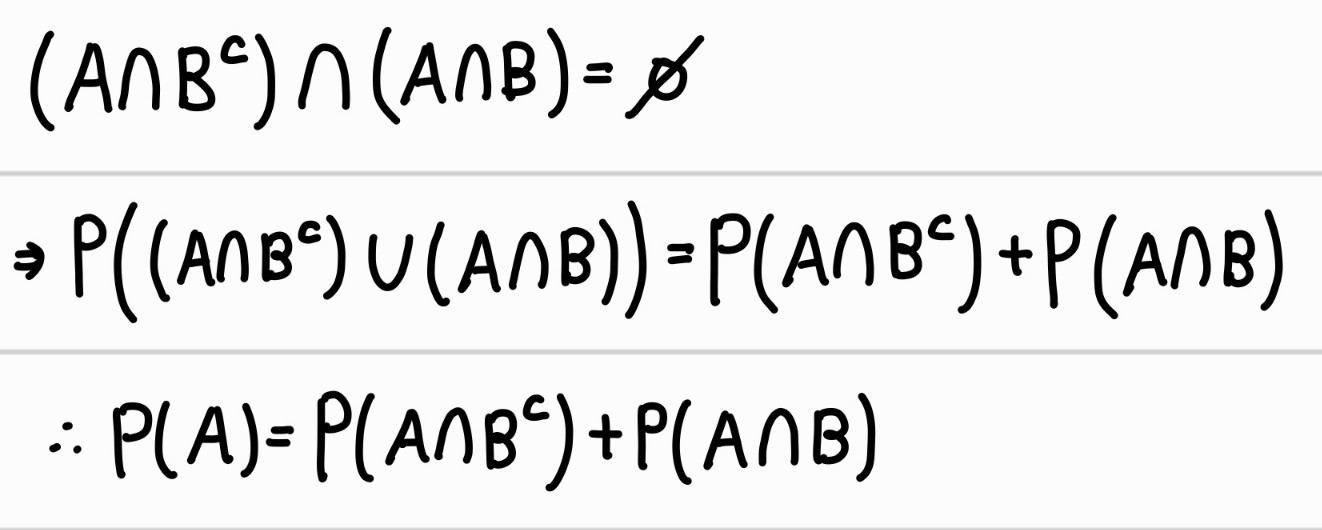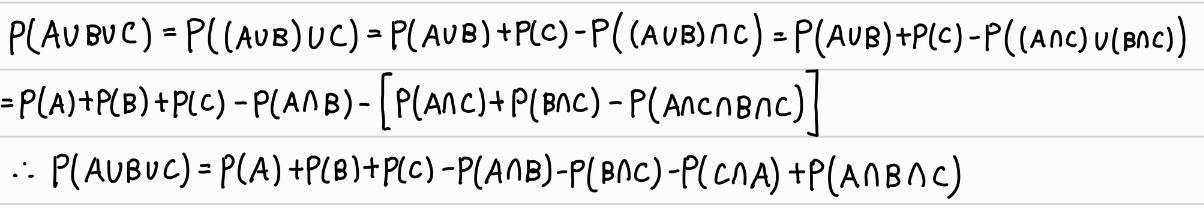확률 공리의 응용 : 파티션, 중요한 항등식

STATS·2023년 6월 16일

수리통계학

목록 보기

3/40

확률 공리의 응용

확률 공리는 확률론의 논리적 기반으로, 이를 통해 여러 정리를 증명하면 유용한 도구들을 얻을 수 있다.
여기서 도구라 함은 실제 세계의 문제를 수학의 영역으로 끌고 올 때, 논리적 오류 없이 도움을 받을 수 있는 항등식, 개념 등을 의미한다.

파티션

다음 조건을 만족하는 표본 공간 $\Omega$ 에 대한 사건들 $A_1, A_2, ..., A_k$ 가 있다고 하자.

$\bigcap_{i=1}^k A_i = \empty$
$\bigcup_{i=1}^k A_i = \Omega$

위 조건은 MECE(Mutually Exclusive, Collectively Exhaustive)라고도 한다.

조건 1.은 어떤 사건도 오버랩되는 경우의 수가 없다는 것을 의미한다. 다시 말해 어떤 사건 집합도 공통된 원소(=시행 결과)를 가질 수 없으므로, 한 사건이 발생할 경우 나머지 $A_i$ 는 모두 발생하지 않는다.

조건 2.는 각각의 사건 집합에 들어 있는 시행 결과들을 모두 모으면 시행의 모든 결과를 표현할 수 있다는 뜻이다. 따라서 시행 결과가 무엇이든 $A_i$ 중 하나는 발생하게 된다.

조건 1과 2를 종합하면, $A_i$ 사건들은 절대 같이 발생하는 경우가 없지만, 반드시 하나는 발생하게 된다는 특이한 성질을 가진다. 이는 파티션이라는 성질이며 후에 다룰 베이즈 정리, 다변량 확률 변수 개념에서 매우 중요하고 요긴하게 사용된다.

이런 조건 아래에서, 표본 공간 $\Omega$ 의 임의의 사건 $B$ 에 대해 다음 정리는 참이다.

P(B) = P(A_1 \cap B) + P(A_2 \cap B) + ...+P(A_k \cap B) = \sum_{i=1}^k P(A_i \cap B)

증명

예를 들어 무작위로 방에 들어오는 사람의 키를 측정하는 확률 시행을 한다고 하자.
그렇다면 $\Omega = \{(h, s) \lvert 0 < h \le 250, \ h \in \R, s \in \{"Male", "Female"\}\}$ 로 키와 성별에 대한 표본 공간을 설정할 수 있다.

물론 키가 250 이상인 사람이 존재한다면 이 표본 공간은 잘 정의된 표본 공간이 아니지만, 예시를 위해 그런 사람은 없다고 하자.

$A_i = \{(h, s) | 10 * (i-1) < h \le 10 * i, \ s \in \{"Male", "Female"\} \}$ 로 정의하자. $A_i$ 는 10cm 구간으로 표본 공간을 자른 사건들이 된다. (단 $1 \le i \le 25$ )

$A_i$ 는 위의 파티션의 두 조건을 만족한다. 따라서 파티션의 성질을 사용할 수 있게 된다.
사건 $B$ 를 "피측정자가 남자인 사건"으로 정의하면, $A_i \cap B$ 는 "피측정자가 남자이고, 키가 $10 * (i-1)cm$ 초과 $(10 * i)cm$ 이하인 사건"이 된다.