수리통계학

내일 날씨, 주식의 등락, 스포츠 경기의 승패처럼 우리의 일상에 큰 영향을 미치지만, 실제로 일이 일어나기 전에는 결과가 불확실한 사례들이 많다. 기상청에서 일기 예보를 해도 틀리는 경우가 많고, 반드시 오를 거라 생각한 종목이 속절없이 떨어지는 경우가 부지기수다. 이

사건과 확률 확률론에서는 사건에 확률을 부여하고, 이를 통해 사건 간의 관계성을 파악하거나 더 발전된 확률론의 개념으로 연결한다. 사건의 언어적인 정의 측면에서 보자면, 사건에 확률을 부여하는 것은 굉장히 직관적이다. "내일 비가 올 확률이 20%야"라는 일상적인 말

확률 공리의 응용 확률 공리는 확률론의 논리적 기반으로, 이를 통해 여러 정리를 증명하면 유용한 도구들을 얻을 수 있다. 여기서 도구라 함은 실제 세계의 문제를 수학의 영역으로 끌고 올 때, 논리적 오류 없이 도움을 받을 수 있는 항등식, 개념 등을 의미한다. 파티션

표본 공간의 축소 세상은 너무 복잡하다. 대부분의 확률 시행은 많은 결과들을 내포하고 있어 쉽게 분석하기가 힘들다. 만약 시행의 결과들 중 일부만 떼어서 관찰할 수 있다면 분석의 복잡성을 낮추는 데 용이할 것이다. 예를 들어 수학과 영어 점수를 측정하는 시행이 있다고

지금까지 예시로 봤던 확률 시행의 결과들, 즉 표본 공간의 원소들은 숫자가 아닌 경우도 있었다. 그러나 이런 경우 시행에 대해 수학적으로 분석하는데 한계가 있게 된다.따라서 확률론에서는 표본 공간의 원소들을, 일련의 숫자들로 바꾸는 작업을 진행한다. 이 변환 과정의 규

확률 변수의 확률 함수 확률 변수의 서포트가 표본 공간이라면, 새로운 사건(서포트의 부분 집합)도 정의할 수 있다. 새로운 사건이 정의된다면, 이들에 대한 새로운 확률도 부여할 수 있을 것이다. 따라서 서포트의 사건들에 확률을 부여할 확률 함수를 새로 정의해야 한다.

확률 변수 $X$의 확률 함수나 분포 함수를 알고 있다고 할 때, $X$에 관한 함수 $Y = g(X)$의 분포를 알고 싶은 경우가 있다. $X$의 분포 정보를 바탕으로 $g(X)$의 분포를 알아내는 과정을 확률 변수의 변환이라고 한다. 확률 변수의 변환은 다양한 분포

확률 변수는 표본 공간의 사건들을 연구자의 관심에 맞게 숫자로 재구성하는 기준의 역할을 한다. 그런데 보통 한 실험에 대해 오직 하나의 관심을 가지는 경우는 적을 것이다.예를 들어 학생의 수능 성적을 표본 공간으로 하는 확률 시행을 한다고 하자. 그렇다면 표본 공간 $

다변량 누적 분포 함수 다변량 확률 분포에서도 일변량 확률 분포와 동일하게 누적 분포 함수(CDF)가 존재한다. 정의도 일변량에서와 동일하지만, 확률 변수가 여러 개라는 것만 다르다. $$ F{X1, X2, ..., Xn} (x1, x2, ..., xn) = P(X1

주변 확률 함수 결합 확률 함수는 $n$개의 확률 변수를 모아 놓은 확률 벡터에 대한 확률 함수로 생각할 수 있었다. 반대로 결합 확률 함수를 알고, 그 중 한 확률 변수의 확률 함수를 알고 싶을 때는 주변 확률 함수를 이용하면 된다. 예를 들어 $f{X1, X2, .

확률 변수 $X, Y$의 독립은 CDF, MGF, PMF/PDF를 이용해 확인할 수 있다.$$X \\perp Y \\\\iff F{X, Y}(x, y) = F_X(x)F_Y(y) \\\\iff f{X, Y}(x, y) = fX(x)f_Y(y) \\\\iff (if \\

베르누이 시행(분포) 확률 변수 $X \ (1 \le i \le n)$가 다음 조건을 만족하면, $X \sim B(p)$라고 한다. 확률 시행의 결과로 $X$는 0과 1 두가지의 값만 가진다. 따라서 시행 결과를 이분법으로 보려는 경우, 예를 들면 성공과 실패, 한

확률 변수열 $X1, X_2, ..., X{y+r}$에 대해 $X_i \\sim B(p), \\ iid$일 때,확률 변수 $Y$를 $Y$ = $r$번 성공까지의 실패 횟수로 정의하면 $Y \\sim NB(r, p)$라고 한다.예를 들어 성공 확률이 1/3인 독립적인 베

포아송 분포는 기준 간격이나 시간, 거리, 공간에서 특정 사건이 발생하는 횟수에 대한 확률 분포다. 예를 들어 1년 동안 태풍이 한국에 직접적으로 닿는 횟수, 08:00부터 17:00까지 학교 정문에 사람이 들어오는 사건의 횟수들을 포아송 분포로 모델링할 수 있다.포아

감마 분포는 지수 분포와 비슷하게 대기 시간, 제품의 신뢰도 등의 확률 분포에 사용된다. 지수 분포가 첫번째 사건이 일어날 때까지의 시간에 대한 확률 분포라고 한다면, 감마 분포는 이를 확장하여 $\\alpha$번째 사건이 일어날 때까지의 시간에 대한 확률 분포를 의미

카이제곱 분포는 $\\alpha = \\frac{r}{2} \\ (r \\in \\N), \\ \\beta = 2$인 경우의 감마 분포를 의미한다. 굳이 감마 분포의 특수한 경우에 이름까지 붙이는 이유는 모분산 추정, 독립성 검정 등 다양한 통계적 검정에서 활용되기 때

정규 분포는 중심 극한 정리와 가설 검정에서 중요한 역할을 하는 통계학의 핵심적인 확률 분포다. 정규 분포의 성질을 도출할 때는 표준정규분포를 이용해 도출하는 경우가 많다.$$Z \\sim N(0, 1) \\ {} \\f_Z(z) = \\frac{1}{\\sqrt{2\

$Z \\sim N(0, 1), V \\sim \\chi^2(r), Z \\perp V$라고 하자. 이 때 T분포는 다음과 같이 정의한다.$$T = \\frac{Z}{\\sqrt{V/r}} \\sim t\_{(r)}$$T 분포의 확률 함수는 다음과 같이 유도할 수 있다

확률 변수 $X$에 관심이 있지만, 정확한 확률 함수 $f_X(x)$를 모른다면 이 확률 함수를 주어진 정보를 이용해 추정할 필요가 있다. 확률 함수를 모른다는 것에는 두가지 상황이 있다. I) X가 어떤 확률 분포를 따르는 지도 모른다는 것과 II) X의 확률 분포(

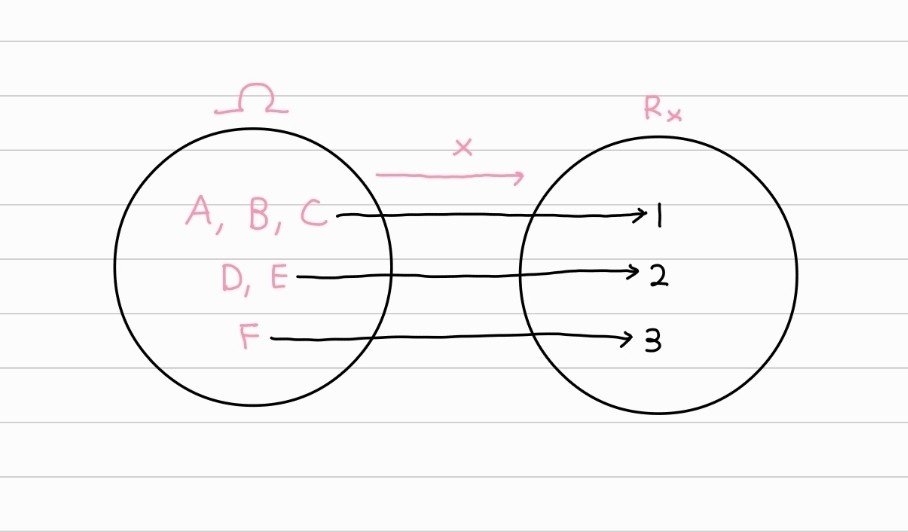
확률변수 $X$가 어떤 분포를 따르는지도 모를 때, 분포의 모수에 의존하지 않는 비모수 추정을 통해 확률 함수를 탐색할 수 있다.$X$가 확률 함수 $p(x)$를 가지는 이산 확률 변수라고 하자. $X_1, X_2, ..., X_n$은 $X$의 랜덤 표본이고, $R_X

점 추정은 직관적이지만 추정량이 실제 모수와 동일할 가능성이 떨어진다. 점 하나로 다른 점을 맞추는 것이기 때문이다.연속형 확률 변수의 경우에는 $P\_\\theta(\\hat{\\theta} = \\theta) = 0$이다. 즉 모수가 $\\theta$의 값으로 주어

$X1, X_2, ..., X_n$을 $N(\\mu, \\sigma^2)$를 따르는 랜덤 표본이라고 하자.$\\bar{X}$, $s^2$이 각각 표본 평균, 표본 분산일 때, 다음과 같은 T분포 확률 변수를 생각할 수 있다.$$T = \\frac{\\bar{X} - \

서포트가 $(a, b)$인 확률 변수 $X$의 랜덤 표본 $X_1, X_2, ..., X_n$이 있다고 하자.이 때 $Y_i\\ (1 \\le i \\le n)$를 랜덤 표본 중 $i$번째로 작은 것이라고 하면, 다음을 만족한다.$$a < Y_1 < Y_2

$Y_1, Y_2, ..., Y_n$이 $a < Y_1 < Y_2 < ...< Y_n < b$를 만족하는 순서통계량이라고 하자.sample range는 표본의 최댓값과 최솟값의 차로, $Y_n - Y_1$으로 정의한다.midrange는 표본의

확률 변수 $X$가 CDF $F(X)$를 가진다고 하자. 이 때 p-백분위수(0 < p < 1)는 $F(\\epsilon_p) = p$를 만족하는 $\\epsilon_p$로 정의한다.즉 p-분위수는 누적된 데이터의 밀도를 나타내는 통계량이다. 예를 들어 $\

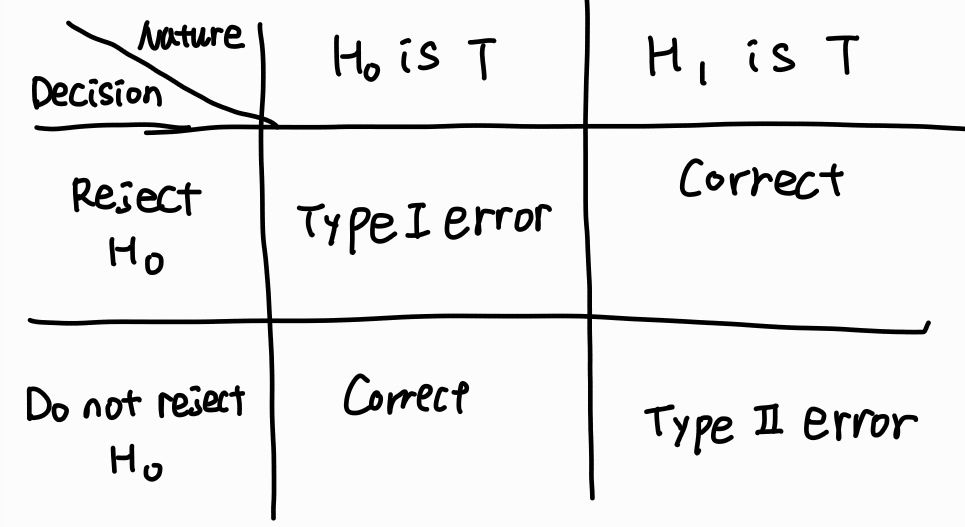
가설 검정 확률 변수 $X$가 관심의 대상이고, $X$의 확률 함수가 $f(x; \theta)$로 주어진다고 하자. 이 때 $\theta$는 $\theta \in \Omega$를 만족하는 모수다. 먼저 가설은 모수의 값에 대한 주장을 의미한다. 예를 들어 $\thet

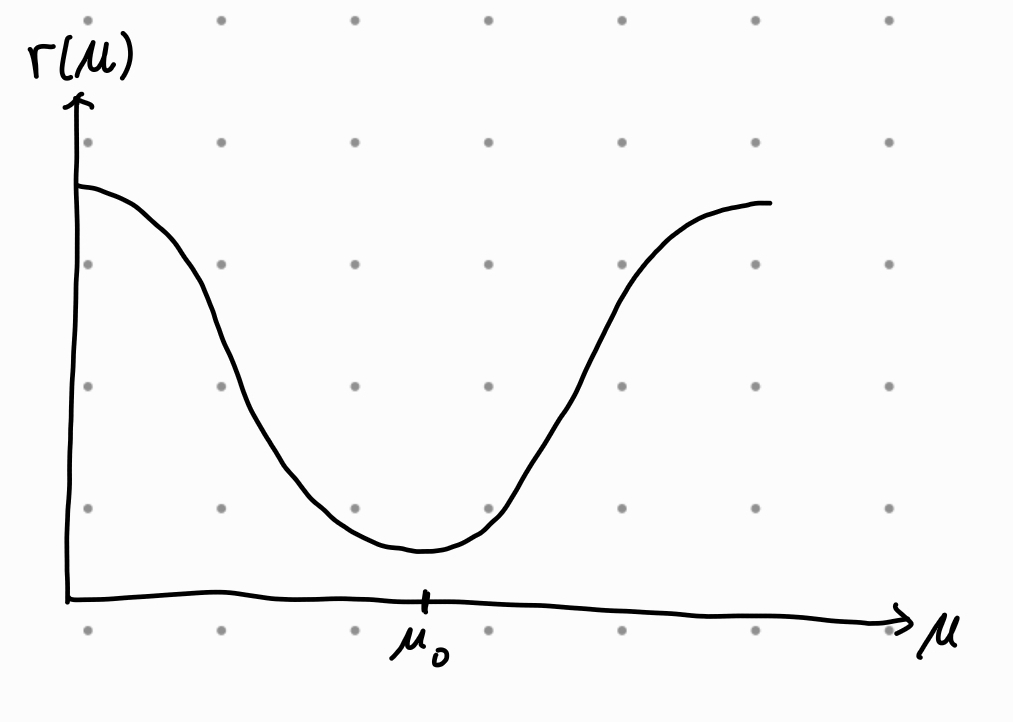
양측 검정 양측 검정과 신뢰 구간의 관계성 p-value

$(X1, X_2, ..., X{k-1}) \\sim multinomial(n, p1, ..., p{k-1})$ 일 때, 표본의 크기가 충분히 크다면 다음 확률 변수는 카이제곱 분포를 근사적으로 따른다.$$Q{k-1} = \\sum{i=1}^k \\frac{(X_i -

확률 변수의 수렴이라는 개념을 잘 이해하기 위해, 배경지식이 되는 실수열의 수렴을 알아보자.실수열 $an$이 상수 $a$로 수렴하면 $lim{n \\rightarrow \\infin}= a$이다.직관적으로 $n$이 커질수록 $a_n$의 값은 $a$ 근처에 존재한다는 것

확률 수렴의 성질 확률 수렴하는 확률변수열은 유용하게 사용될 수 있는 몇가지 성질들을 가진다. 확률 수렴하는 확률변수열의 합 상수배된 확률 수렴하는 확률변수열 x=a에서 연속인 함수 g에 대한 확률 수렴 추정량의 일치성 모수 $\theta$에 대한 추정량 $Tn

${Xn}$이 확률변수열이고, $X$가 확률변수일 때, 각각 $F{X_n}$과 $F_X$를 $X_n$과 $X$의 CDF라고 하자. $C(F_X)$를 $F_X$가 연속인 점들의 집합이라고 할 때,$$\\lim \\limits{n \\to \\infin} F{X_n}(x)

표본공간의 분할(파티션) 베이즈 정리

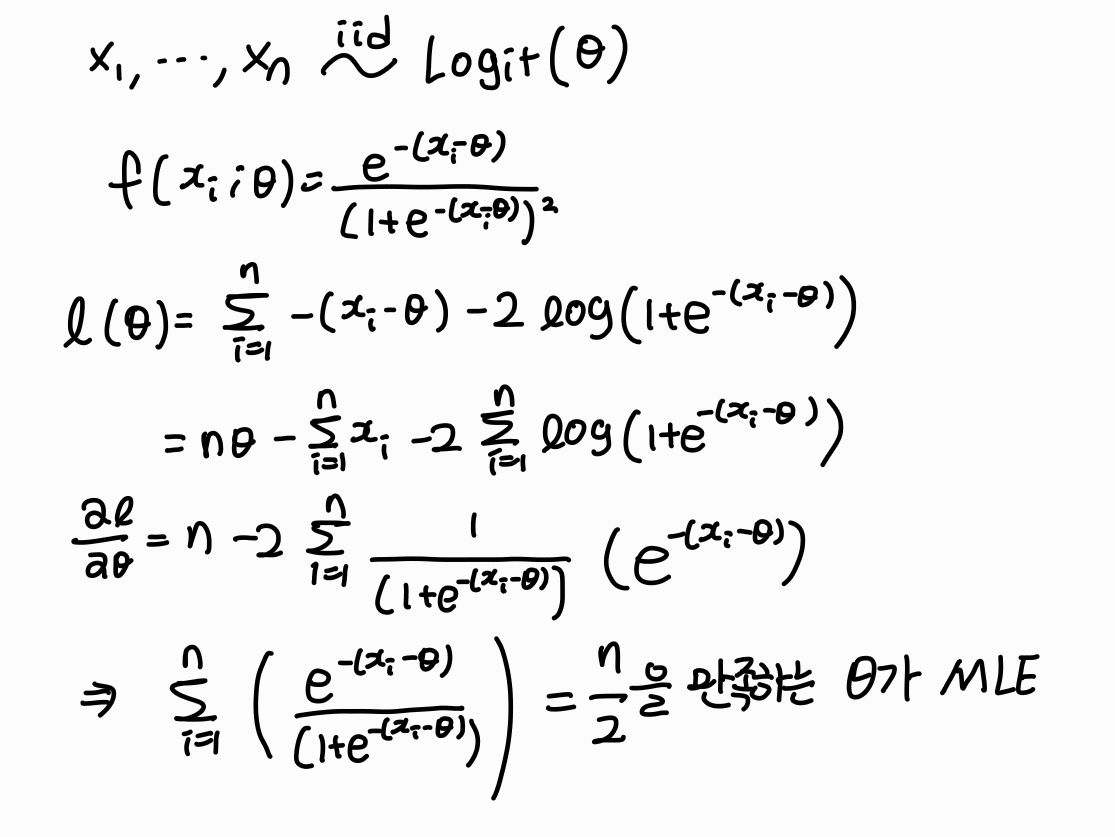
$X_1, ..., X_n$이 동일한 pdf $f(x;\\theta), \\ \\theta \\in \\Omega$에서 각각 독립적으로 추출된 랜덤 표본이라고 하자.$L(\\theta;x) = L(\\theta) = \\prod\_{i=1}^n f(x_i;\\theta

정칙조건 정칙조건은 이론/논리적 전개의 용이성을 위해 가정하는 조건들을 의미한다. 확률 함수들은 $\theta$에 대해 단사다. 즉 $\theta \neq \theta '$이면 $f(xi; \theta) \neq f(xi; \theta ')$이다. 확률 함수들은 가

모수벡터가 $\\theta = (\\theta_1, ..., \\theta_k)$인 확률분포에서 랜덤 표본 $X_1, ..., X_n$을 추출한다고 하자.확률분포의 $r$차 모적률은 $E(X^r)$이다. 만약 MGF가 존재할 경우 $E(X^r) = \\frac{d^r}

추정량도 확률변수이기 때문에 확률시행의 결과에 따라 값이 달라진다. 바람직한 추정량의 경우 추정량의 값이 모수와 거의 비슷해야 모수 추정의 의미가 있다.따라서 모수와 추정량의 거리를 재는 측도를 설정한 후, 그 측도를 바탕으로 추정량의 성능을 평가한다.보통 모수와 추정

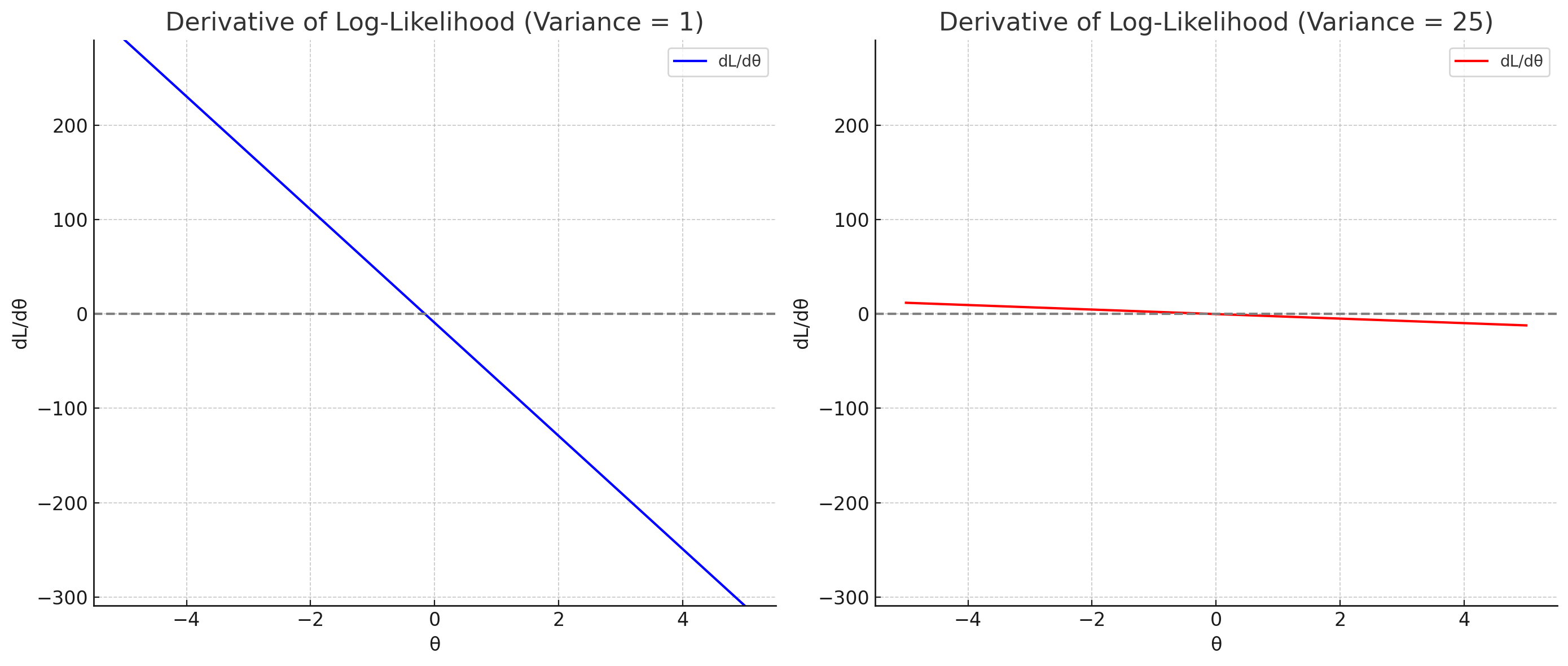
피셔 정보량의 정의는 다음과 같다.$$I(\\theta) = E \\left{\\frac{\\partial}{\\partial \\theta} log f(X ; \\theta)}^2\\right$$피셔 정보량은 흔히 "표본이 모수를 추정하는데 얼마나 많은 정보를 주는가

최소분산비편향추정량(MVUE)는 비편향추정량 중에서 분산이 가장 작은 추정량을 의미한다. 추정량의 모수와의 평균적인 거리를 나타내는 지표인 MSE는 다음과 같이 편향과 분산으로 분리 가능하다.$$MSE = Var(\\hat{\\theta})+(bias)^2$$그런데 비

$X = (X_1, ..., X_n)$의 결합 확률밀도함수가 $f(x_1, ..., x_n; \\theta_1, ... \\theta_k)$일 때, $S(X) = (S_1(X), ..., S_l(X))$를 $l$개의 통계량 벡터라고 하자.이 때 조건부 확률변수 $(X_

$X_1, ..., X_n$의 결합 확률 함수가 $f(x_1, ..., x_n;\\theta)$일 때, $S(X) = (S_1(X), ..., S_k(X))$를 $k$개의 통계량이라고 하자.$S$가 결합충분통계량 $\\Leftrightarrow$ $f(x_1, ...,