확률 변수

확률 변수

지금까지 예시로 봤던 확률 시행의 결과들, 즉 표본 공간의 원소들은 숫자가 아닌 경우도 있었다. 그러나 이런 경우 시행에 대해 수학적으로 분석하는데 한계가 있게 된다.

따라서 확률론에서는 표본 공간의 원소들을, 일련의 숫자들로 바꾸는 작업을 진행한다. 이 변환 과정의 규칙이 되는 함수를 확률 변수라고 한다. 조금 더 엄밀한 정의는 다음과 같다.

확률 시행의 표본 공간 $\Omega$에 대해, 확률 변수 $X$는 다음과 같은 함수다.

즉 확률 변수는 시행의 모든 결과 각각을 규칙에 따라 한 실수에 대응시키는 함수의 역할을 한다.
그리고 $X$의 치역 $\equiv$ $X(\Omega)$를 X의 서포트 / 공간이라고 한다.

예를 들어 게임에서 아이템의 강화를 생각해보자.
$\Omega = \{"강화 \ 성공", "강화\ 유지", "강화\ 실패"\}$
그러나 이 표본 공간은 원소들이 숫자가 아니기 때문에, 확률 변수를 이용해 표본 공간을 숫자로 나타내려 한다.

첫 번째 케이스는 성공과 유지는 1로, 실패는 0으로 변환하는 것이다.

이 케이스에서는 $X$의 서포트가 $\{0, 1\}$이 된다.

그러나 반드시 위와 같이 확률 변수를 정의할 필요는 없다. 다른 케이스를 보자.

따라서 표본 공간에 대한 확률 변수의 정의는 연구자가 탐구하려는 부분에 따라 다르게 정의할 수 있다.

위의 예시에서는 만약 실패하느냐 나머지 결과가 나오느냐가 궁금하다면 첫번째 확률 변수를 이용할 수 있고, 각 결과에 따라 가중치를 다르게 주고 싶다면 두번째 확률 변수를 이용할 수 있다.

주의할 점은 확률 변수는 확률과는 관련이 없는 함수다. 확률 변수의 역할은 오직 각 시행 결과를 특정한 실수로 대응하는 것이다. 따라서 대응시키는 실수는 0과 1 사이뿐만 아니라 음수, 매우 큰 수가 될 수도 있다.

확률 변수와 실제 확률의 관계에 대해서는 뒤의 '확률 변수와 확률 함수'에서 다룬다.

확률 변수 : 변수 vs 함수?

확률 변수는 분명히 이름은 변수인데 역할은 함수라고 하는 것이 앞 뒤가 맞지 않아 보인다.

이를 이해하기 위해 함수 $f(x)$를 생각해보자. $f(x)$는 각각의 x를 다른 값들로 대응하는 함수의 역할을 한다. 그러나 x가 정해지고 나면, $f(x)$는 하나의 값의 역할을 하기도 한다.
즉 f(x)는 x의 값에 따라 값이 달라지는 변수의 성질과, x를 다른 값으로 대응하는 규칙이라는 함수의 성질을 모두 가지고 있는 것이다.

이 관점에서 볼 때, 확률 변수 $X$를 동일한 맥락으로 이해할 수 있다.

1. 확률 변수 X의 변수의 성질
   확률 변수 X는 확률 시행의 결과로 $s \in \Omega$가 정해지고 나면, $X(s)$는 하나의 값으로 정해진다. 보통 $X(s)$를 $X = X(s)$로 표현하므로, $X$는 시행의 결과에 따라 달라지는 변수의 특성을 가진다.

2. 확률 변수 X의 함수의 성질
   위에서 봤듯이 확률 변수는 표본 공간의 각 원소를 실수로 대응하는 함수의 역할을 한다. 따라서 이 경우 $X$는 함수의 성질을 가진다.

확률 변수 : 표본 공간의 파티션

표본 공간 $\Omega$의 각 원소(시행 결과) 각각은 서포트의 한 숫자로 대응된다.
반대로 서포트의 입장에서 $\Omega$를 바라보면, 서포트의 각 숫자들이 $\Omega$의 부분 집합으로 대응한다고 볼 수 있다.

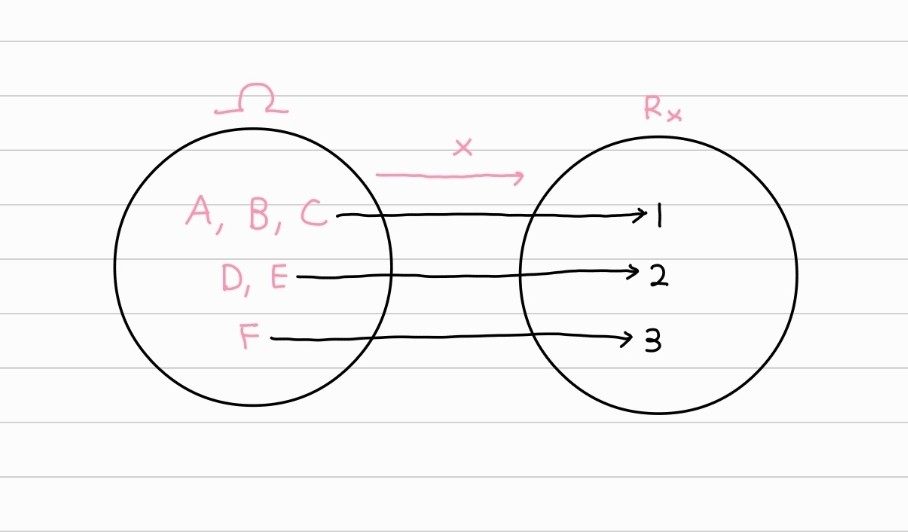예를 들어 위와 같이 A, B, C가 1로 대응하고, D, E가 2로 대응하고 , F가 3으로 대응하는 확률 변수 X가 있다고 하자.

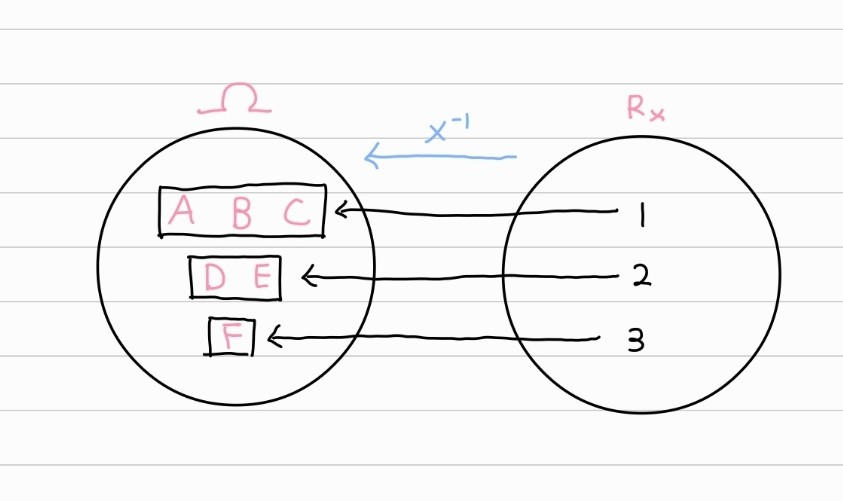그렇다면 서포트의 입장에서는 각 값이 표본 공간의 부분 집합(사건)으로 대응된다. 더 중요한 특성은 이렇게 대응하는 사건들은 모두 파티션을 이룬다는 것이다.

이는 표본 공간의 값들이 서포트로 1. 모두 대응되고, 2. 오직 한 값으로 대응되기 때문에 생기는 특성이다.

새 표본 공간으로서의 확률 변수

서포트를 곧 표본 공간의 파티션으로 생각할 수 있다는 것은 중요한 의미를 가진다.
이렇게 되면 서포트 자체를 시행의 새로운 표본 공간으로 사용할 수 있기 때문이다.

이 것이 중요한 이유는 복잡한 표본 공간을 연구자의 관심에 따라 의미있는 숫자들로 변환할 수 있고, 혹은 표본 공간을 몇 개의 숫자로 단순화 할 수 있기 때문이다.