[BOJ/Python] 1182 부분수열의 합

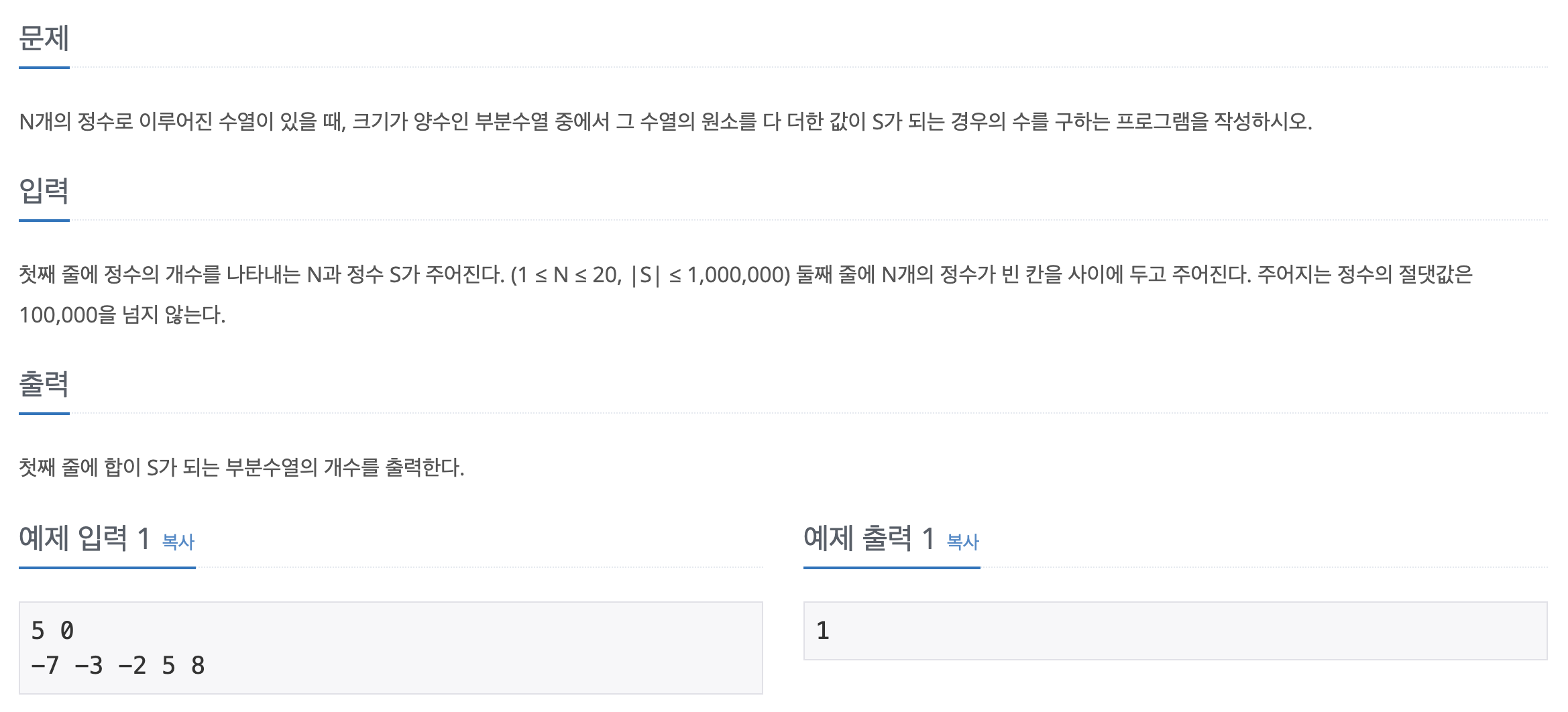
📌 문제

[백준] 1182 부분수열의 합

📌 풀이

1. 완전 탐색 가능 여부 판단

문제에서 수열의 개수는 총 N개, 최대 20개.
부분 수열을 만드는 경우의 수는 N개의 원소 각각을 선택하냐/마냐의 문제이므로 가능한 경우의 수는 2^20 = 약 100만개.
이는 시간 제한 안에 모두 탐색할 수 있는 충분한 개수!
(CPU에 따라 차이가 있긴 하지만, 일반적으로 1초 동안 약 1억번의 연산이 가능함.)

cf) 부분 수열은 반드시 연속되어야 하는 것은 아님!

2. 부분 수열 만들기

재귀 함수 사용하기!

0번째 원소부터 N-1번째 원소들에 대해 배열에 포함할지 안할지를 재귀적으로반복해서 부분 수열 만들기
해당 문제에서는 부분수열의 "합"이 중요하므로, 현재까지 구한 수열의 합을 재귀로 넘겨주면서 탐색하면 된다.
탐색한 원소의 개수가 N개가 되면 탐색을 종료하고, 현재 합이 S와 일치한다면 정답값에 +1 해준다.

📌 코드 설계

1. 문제의 입력값 받기
2. 재귀 함수: 모든 부분 수열 탐색하기
3. 정답 출력하기

📌 정답 코드

from itertools import combinations

# 입력
N, S = map(int, input().split())
numbers = list(map(int, input().split()))

# 부분수열의 합이 S인 경우의 수를 저장하는 변수
answer = 0

# 모든 부분수열의 조합 탐색
for r in range(1, N + 1):  # 부분수열의 길이를 1부터 N까지 탐색
    for subset in combinations(numbers, r):  # r개의 원소를 가지는 부분수열 생성
        if sum(subset) == S:  # 부분수열의 합이 S인지 확인
            answer += 1

# 출력
print(answer)