[BOJ/Python] 2210 숫자판 점프

📌 문제

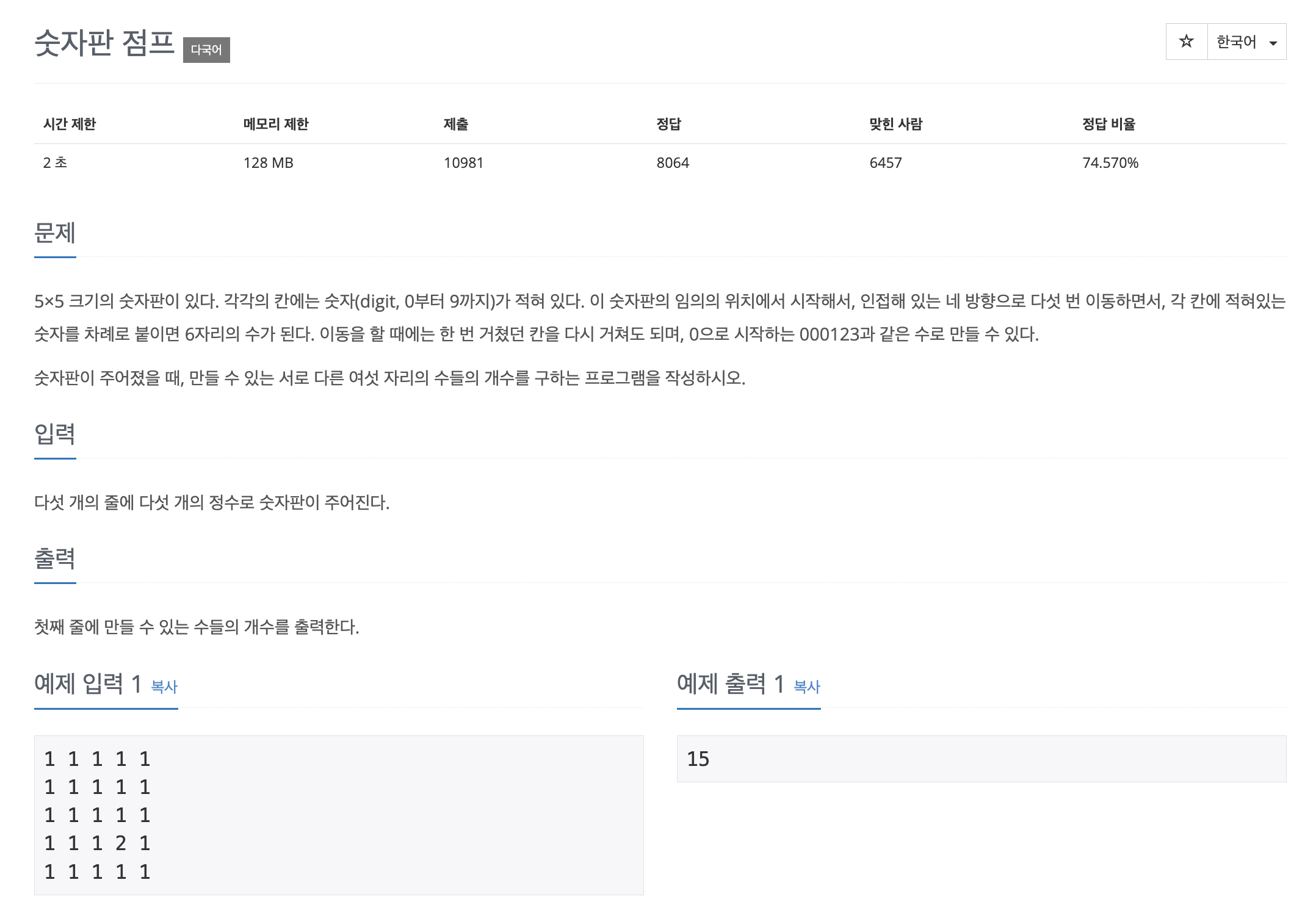
[백준] 2210 숫자판 점프

📌 풀이

1. 완전 탐색 가능 여부 판단

• 시작 위치: 25개의 경우 (5*5 숫자판의 임의의 위치에서 시작하므로)
• 이동: 4^5 (네 방향으로 5번 이동하므로)
• 총 경우의 수: 25*4^5 = 25600 ⇒ 충분히 완전 탐색 가능!

2. 완전 탐색 구현

1. 임의의 위치 (x, y) 에서 시작하기
2. 다섯 번 이동하면서 해당 위치의 숫자를 string에 이어 붙이기
3. string의 길이가 6이 되면 탐색 중단하기
4. 각 위치에서 상/하/좌/우로 이동하는 경우를 재귀로 탐색하기
   • 해당 문제에서는 한 번 거쳤던 칸도 다시 거칠 수 있으므로 DFS 와 달리 방문 여부 기록할 필요 X
   • 💡 상하좌우 이동 팁: dx = [-1, 1, 0, 0], dy = [0, 0, -1, 1] 을 만들어 놓고 사용하면 한 노드의 상,하,좌,우 위치를 쉽게 계산 할 수 있음!

      for i in range(4):
          nx = x + dx[i]
          ny = y + dy[i]

📌 코드 설계

1. 문제의 입력값 받기
2. 재귀 함수: 다섯 번 이동하는 탐색 구현하기
3. 탐색 진행하기
4. 정답 출력하기

📌 정답 코드

import sys

board = []
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]

# 1. 입력값 받기
for _ in range(5):
    arr = sys.stdin.readline().split()
    board.append(arr)
    
answer = set()

# 2. 재귀 함수: 다섯 번 이동하는 탐색 구현하기
def dfs(x, y, now):
    now += str(board[x][y])
    if len(now) == 6: # answer 의 길이가 6이 되면 탐색 중단
        answer.add(now)
        return
    
    for i in range(4):
        nx = x + dx[i]
        ny = y + dy[i]
        
        if nx < 0 or nx >= 5 or ny < 0 or ny >= 5:
            continue
        dfs(nx,ny,now)
    

# 3. 탐색 진행하기
for i in range(5):
    for j in range(5):
        dfs(i,j,"")


# 4. 정답 출력하기
print(len(answer))