★ [LeetCode/Python] 42. Trapping Rain Water

📌 Problem

[LeetCode] 42. Trapping Rain Water

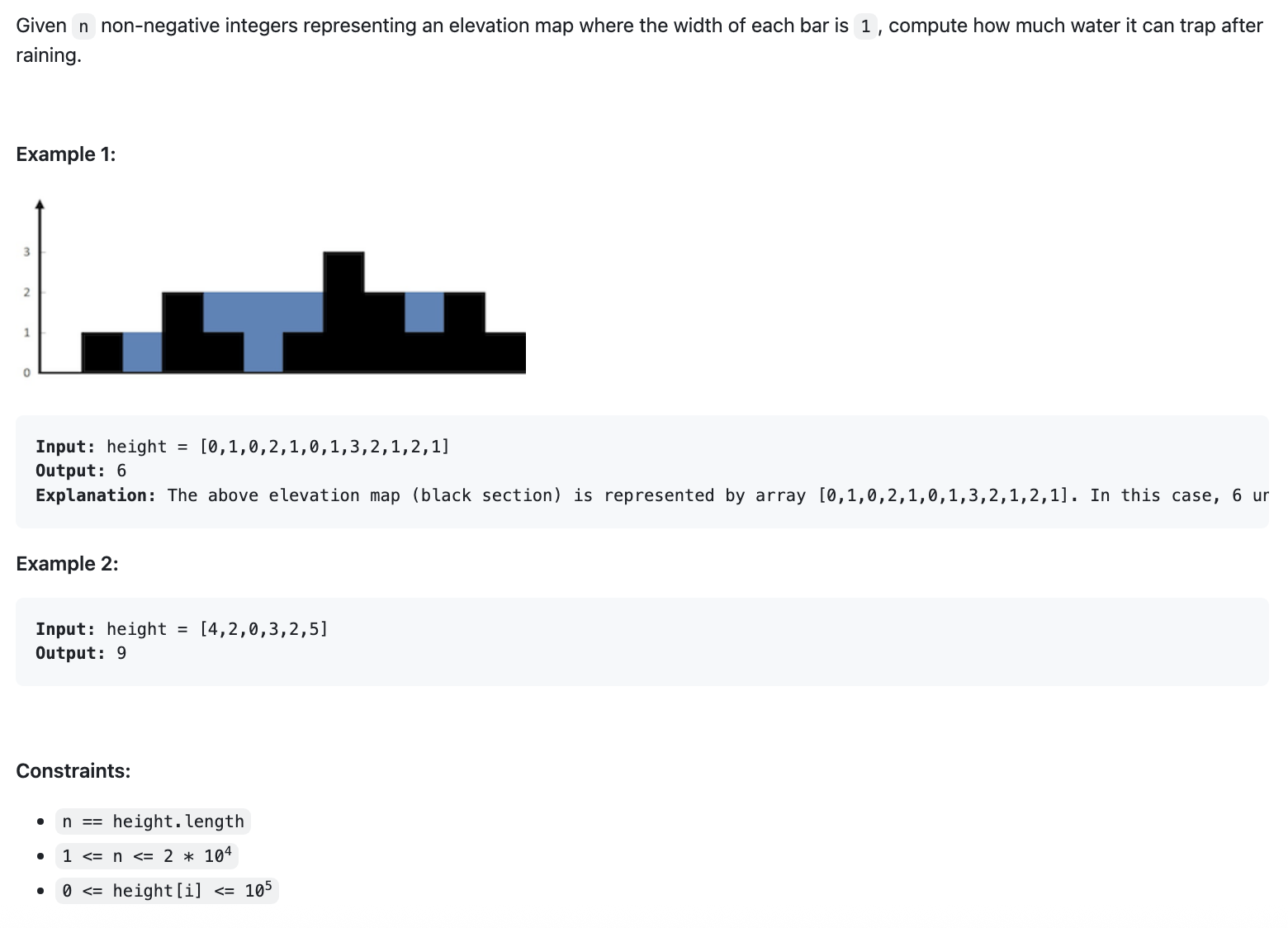
📌 Solution

Idea

칸 i 위에 고일 물의 높이:

$\min(\text{leftMax}_i, \text{RightMax}_i) - \text{height}_i$

여기서 $\text{leftMax}_i$는 왼쪽(포함)에서의 최대 높이, rightMax_i는 오른쪽(포함)에서의 최대 높이에 해당함.
즉, 양쪽 벽 중 더 낮은 벽이 물 높이를 결정함.

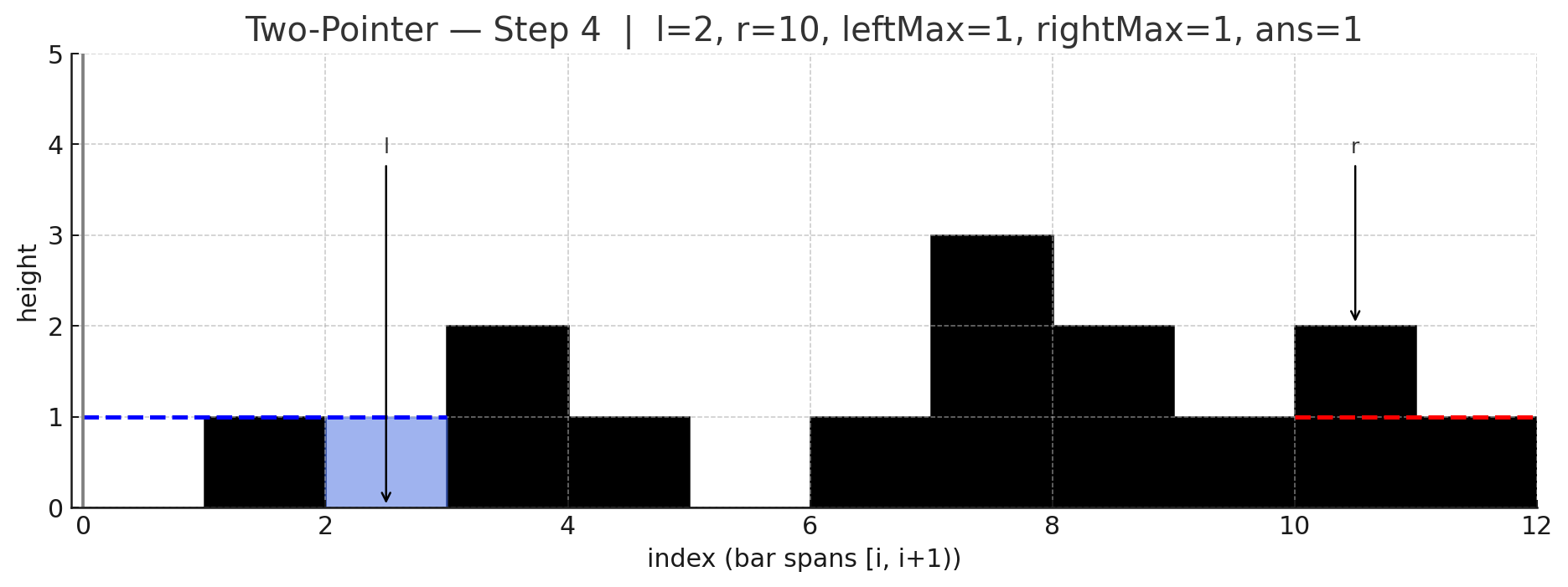
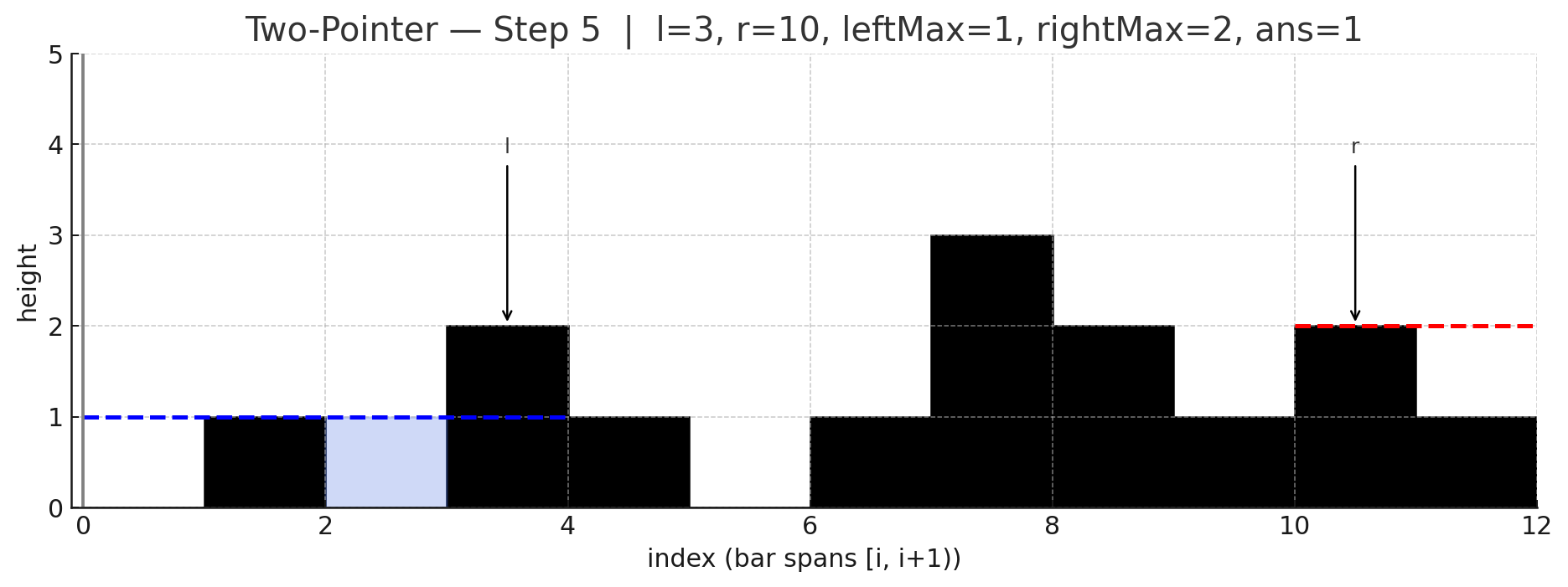
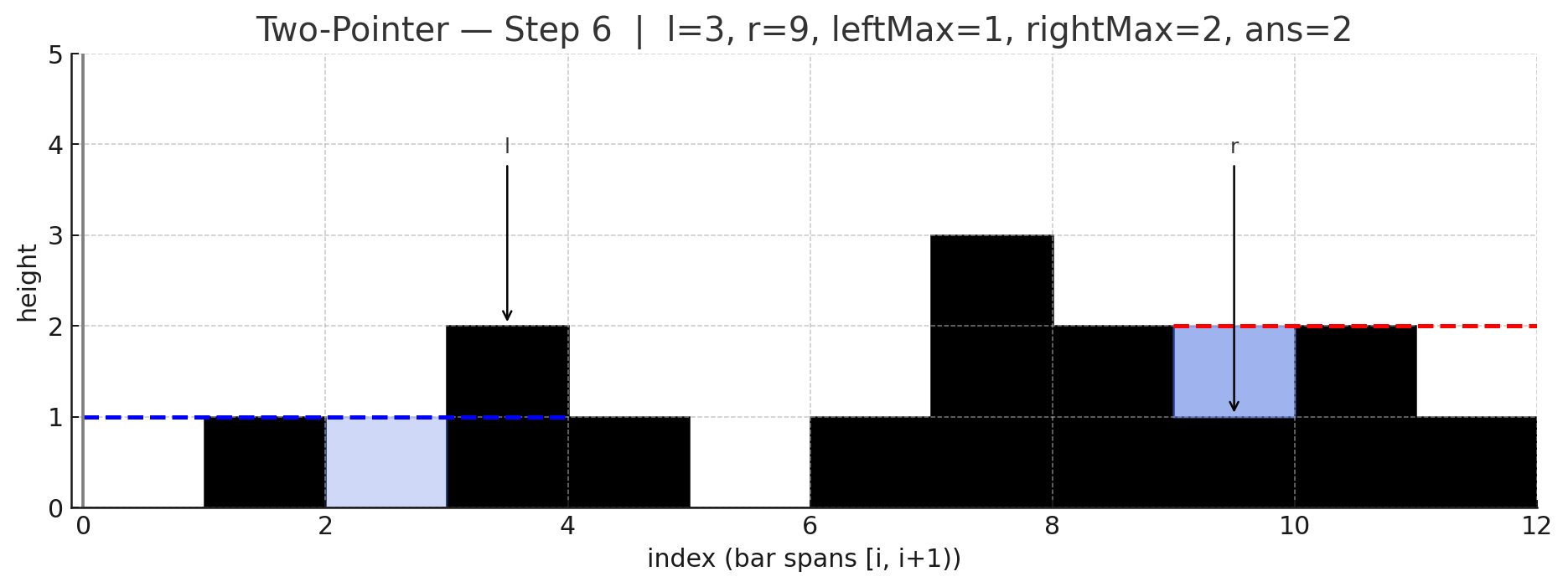
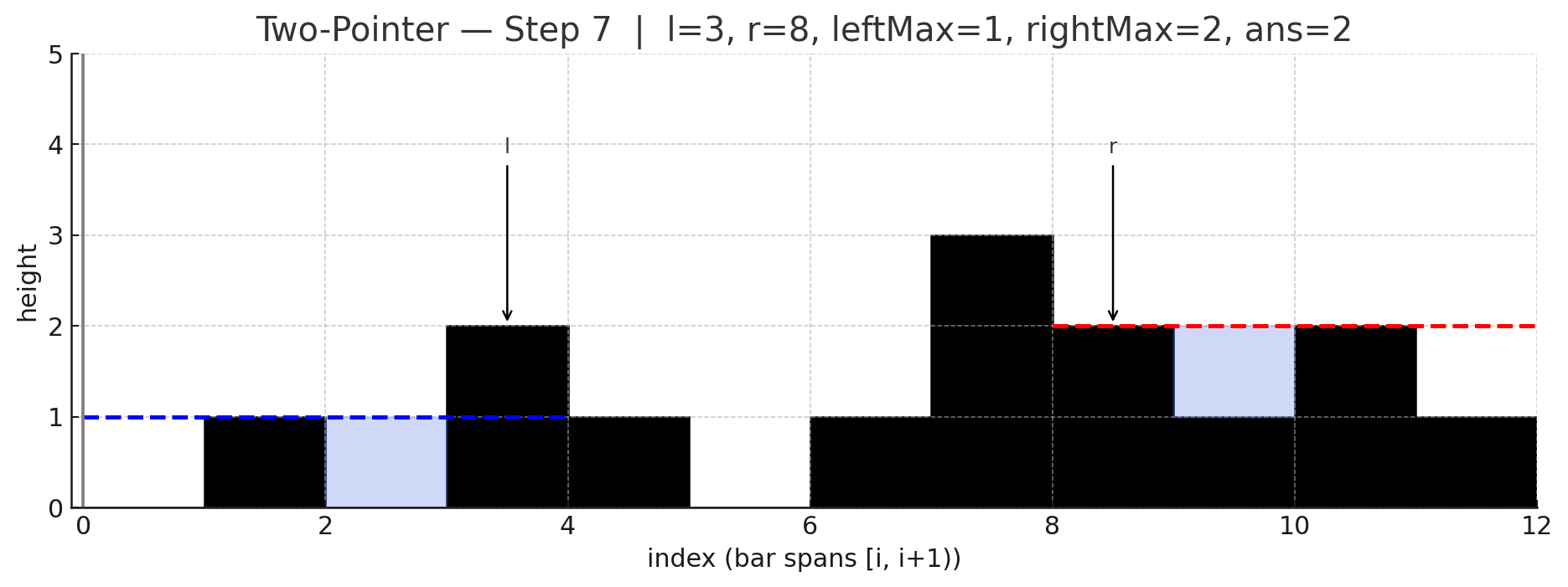
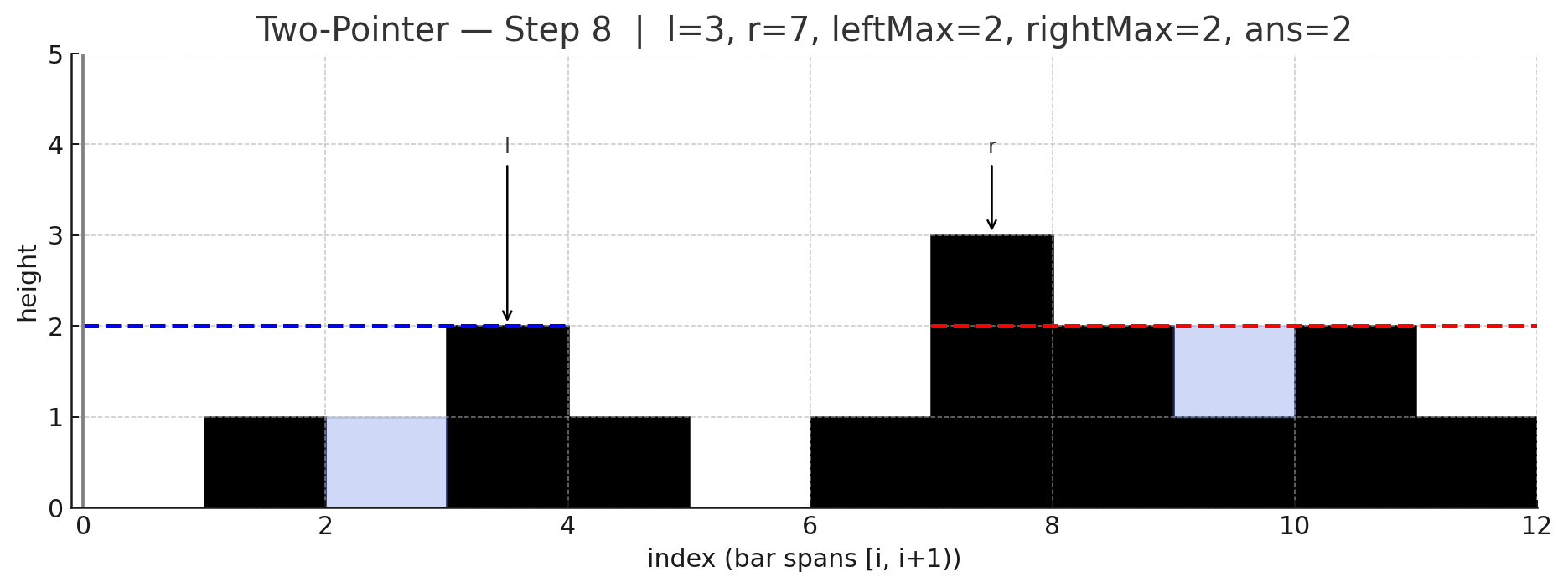
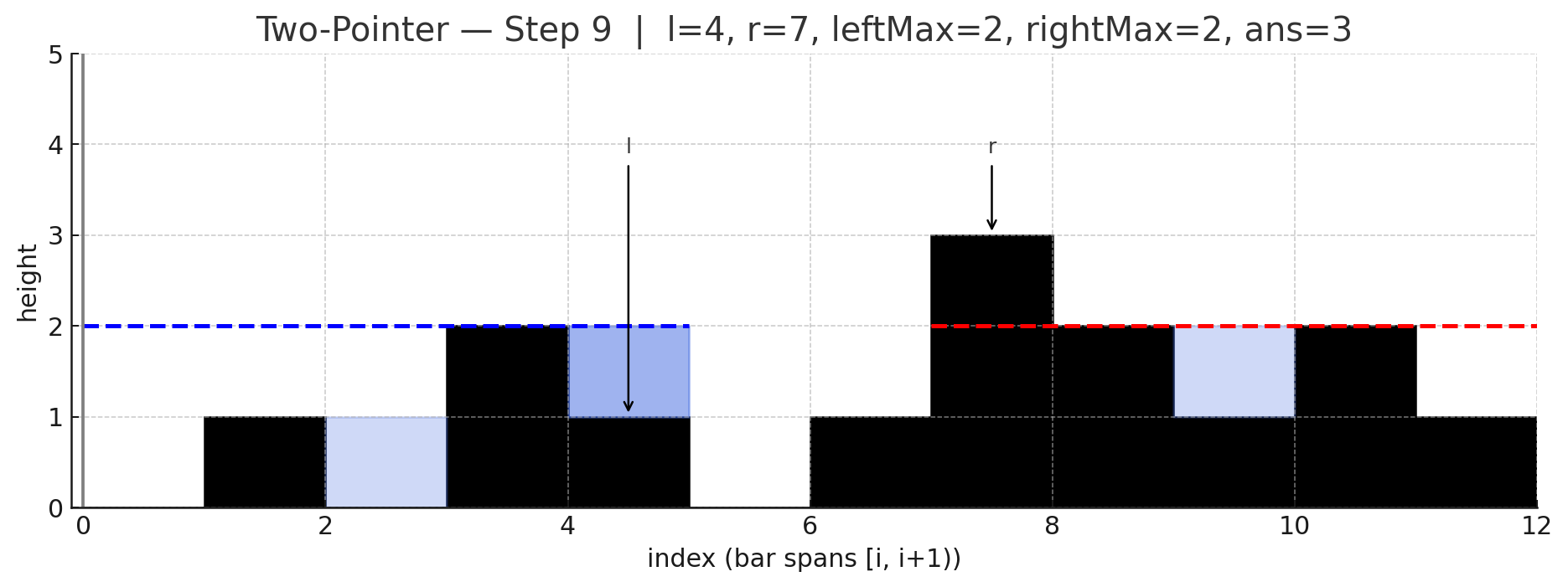
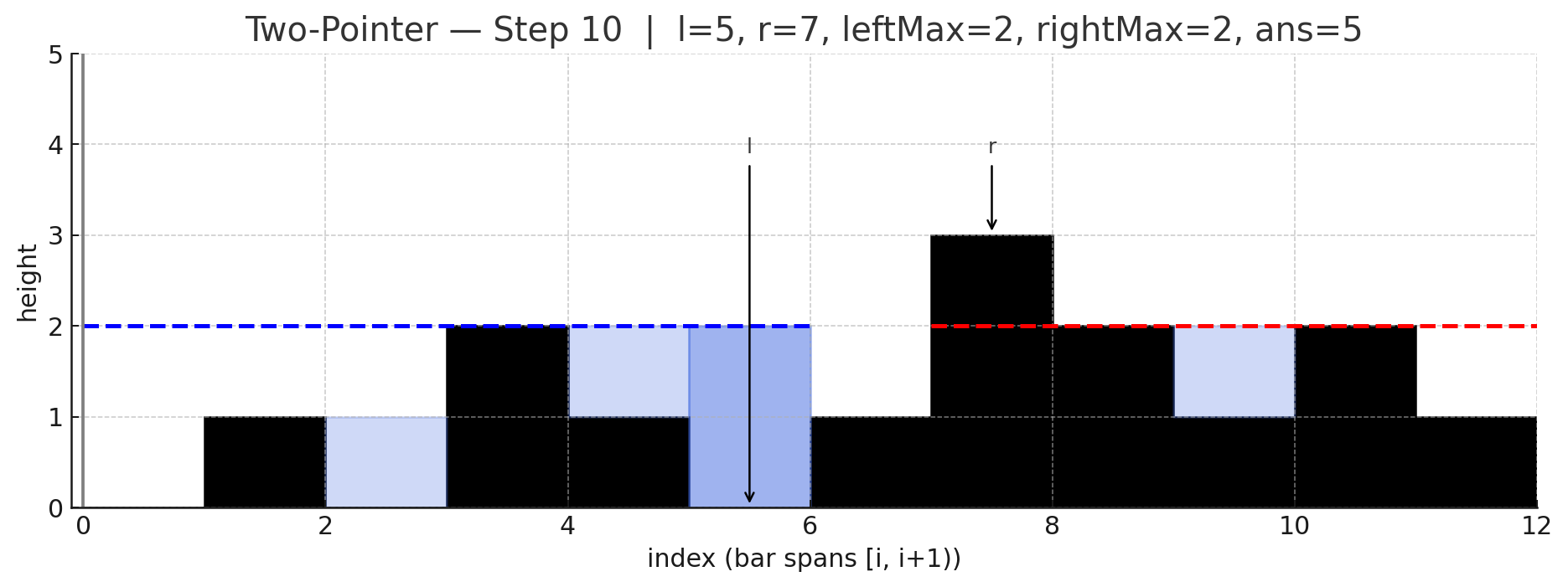
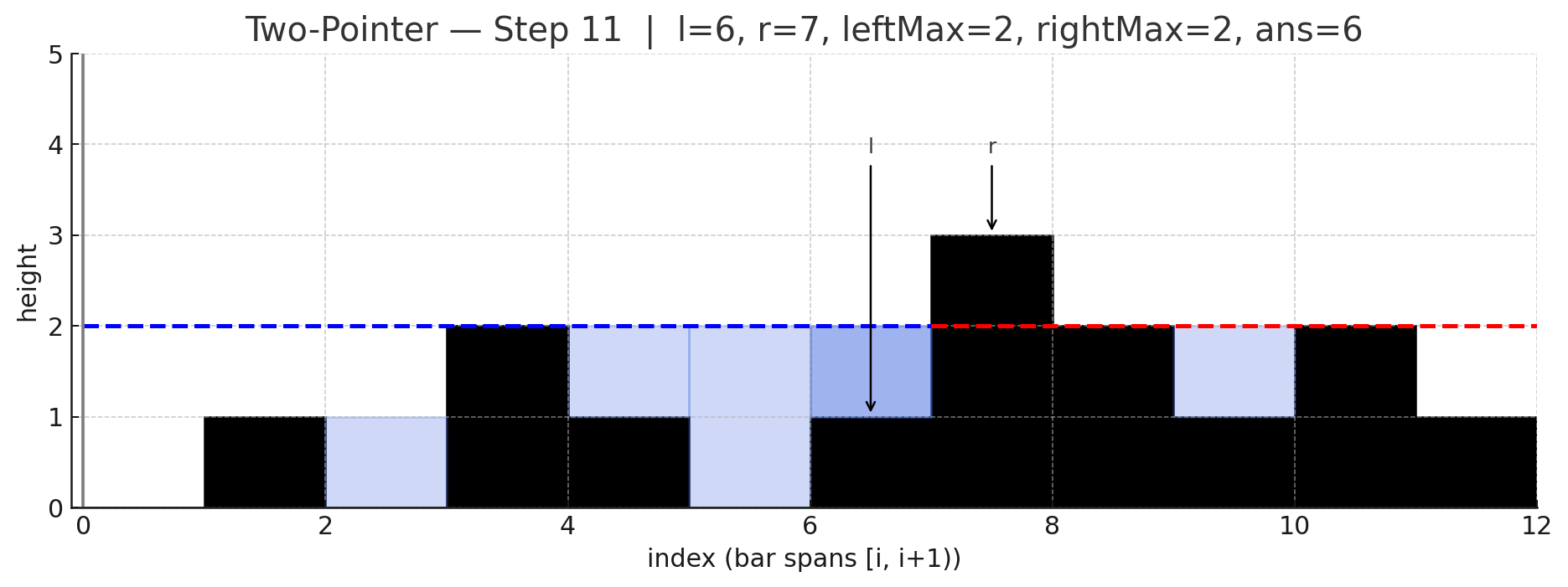
두 포인터 아이디어는 양끝에서 시작해 더 낮은 쪽을 한 칸씩 확정지어가며 처리하는 것인데, 낮은 쪽은 이미 반대편에 "그보다 낮지 않은 (= 더 높거나 적어도 같은 높이의) 벽"이 존재하므로, 그 위치의 물 높이는 자기 쪽 최대 높이만으로 안전하게 계산할 수 있음.

포인터 l(왼쪽), r(오른쪽), 그리고 현재까지의 leftMax, rightMax를 유지함.

만약 height[l] < height[r]라면, 오른쪽에는 최소 height[r] 높이의 벽이 존재함을 의미하므로, 이때 l 위치의 물 높이는

⁡$\min(\text{leftMax}, \text{RightMax}) - \text{height}_l$

인데, rightMax ≥ height[r] > height[l]이므로 좌측에서 가능한 물 높이는 leftMax에 의해 제한됨.
따라서 l에서 더 높은 오른쪽 벽을 "기다릴 필요 없이" 지금 leftMax - height[l]를 더해도 됨을 알 수 있음. 이후 더 오른쪽으로 가며 rightMax가 커져도 min(leftMax, rightMax)의 최소값은 이미 leftMax였기 때문에 l의 물량이 바뀌지 않음.

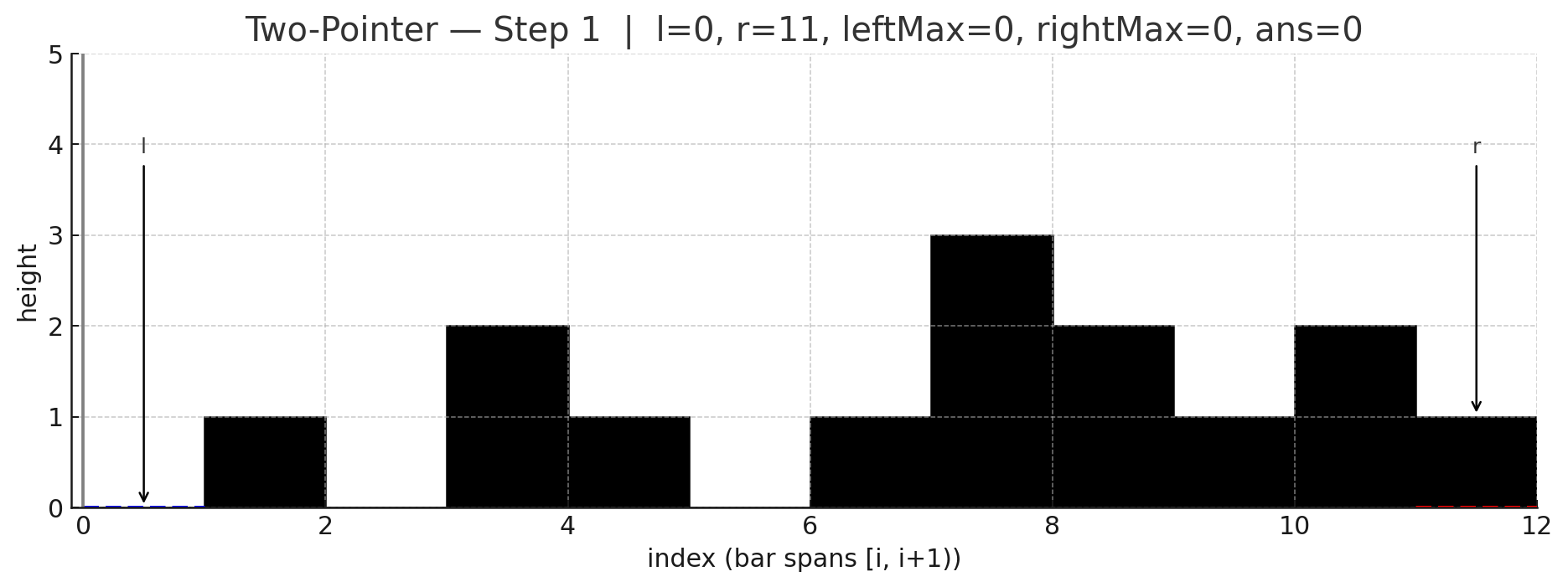
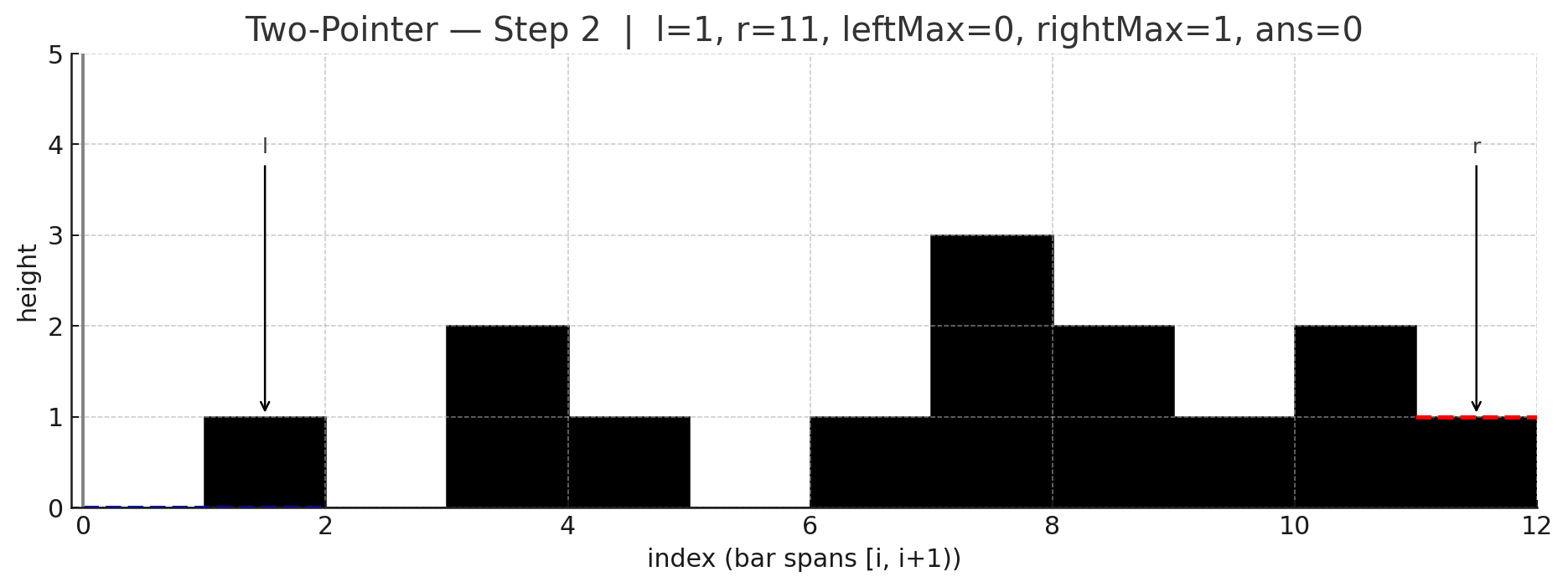
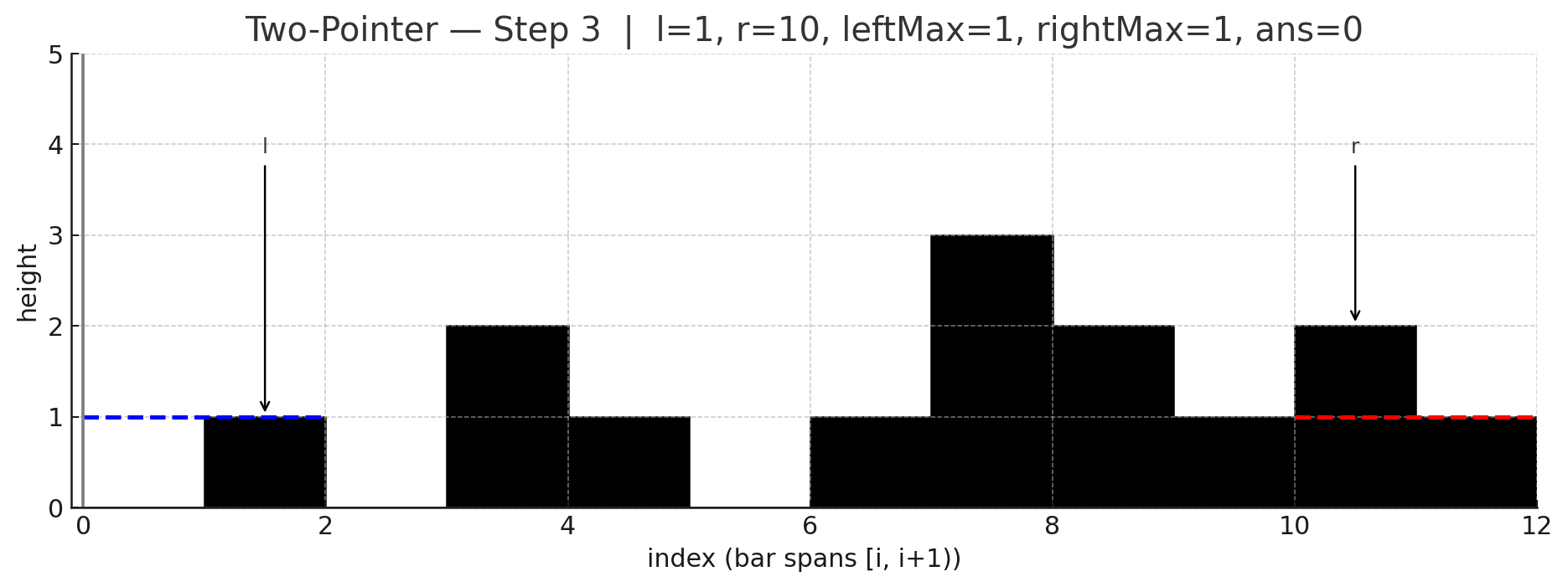
Code

class Solution:
    def trap(self, height: List[int]) -> int:
        l, r = 0, len(height) - 1
        leftMax = rightMax = 0
        ans = 0

        while l < r:
            if height[l] < height[r]:
                leftMax = max(leftMax, height[l])
                ans += leftMax - height[l]
                l += 1
            else:
                rightMax = max(rightMax, height[r])
                ans += rightMax - height[r]
                r -= 1
        return ans