chapter 5 recap
-
지난 강의에서는 value function에 parameter 추가 -> 여기서 한 방식으로 policy 탐색
-
이번 강의에서는 policy를 직접 parameterise 하는 방식 사용
-
하지만 policy based function은 value function을 계산하지 않으므로 그 action을 취할 당시 value를 계산하지 않는다
-
앞서 배운 value based, 이번 장에서 배운 policy based 그리고 그 교집합은 아래와 같은 관계를 갖는다.
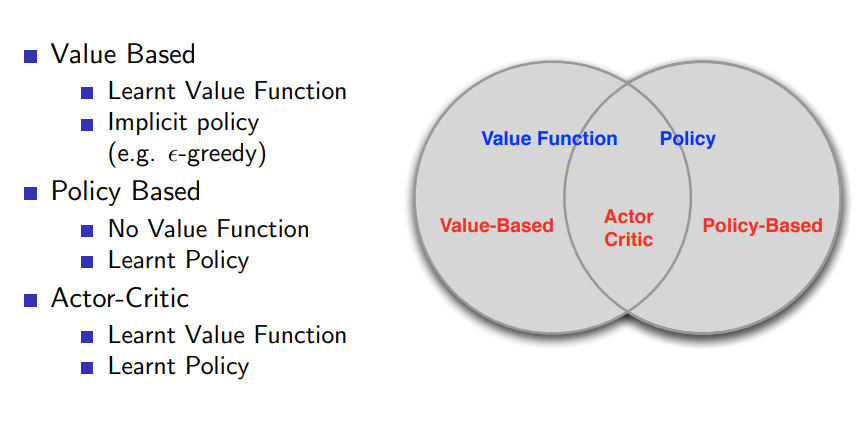
-
장점
- 수렴을 더 잘함
- action space 가 high dimensional 하고 continuous 한 경우 유리
- stochastic policy를 배울 수 있음
- 단점
- global 이 아닌 local optimum에 수렴함
- policy를 evaluation 하는 것은 inefficient 하고 high variance를 가짐
- stochastic policy를 배워 유리한 예시는 아래와 같다.
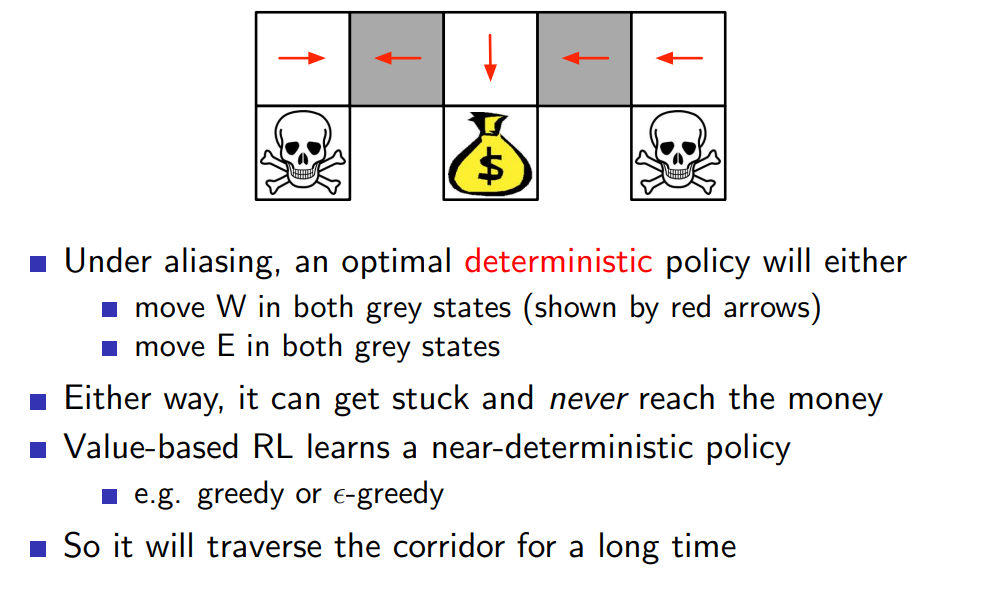
deterministic policy 같은 경우 두 grey grid를 구분하지 못해 같은 action을 유도하여 원하는 위치에 도달할 수 없지만 stochastic policy를 배운다면 이를 해결할 수 있다. 앞선 장에서 배운 value-based RL은 near deterministic policy를 제시하기 때문에 grey grid가 속한 row에서 오랜 시간을 보낼 것이다.
Objective function
- policy based RL에서 목표가 되는 함수는 어떤 것일까 (이 함수는 policy의 효과를 measure 할 수 있어야 한다)
세 가지 방법이 가능하며 아래와 같다.

- start state의 value function을 objective로 잡아 향 후 기대되는 return 을 최적화한다.
- 각 state에 대한 value function의 평균을 대상으로 설정한다
- 부분은 state s에서 가능한 action a에 대해 그 것을 취할 확률과 reward를 곱해 그 state에서 얻을 수 있는 평균적 reward 값을 의미하며 앞에 를 곱해 전체적으로는 모든 state에 대한 average를 구하게 된다.
Policy optimisation and Gradient
-
앞선 장의 value function gradient 방식과 비슷하게 에 대해 를 최대로 만드는 를 찾는 것이 목적이다.
-
하지만 앞 과의 차이점은 의 maximization이기 때문에 gradient ascent를 해야 한다는 점이다. 그 값은

위와 같다. -
위의 policy gradient를 계산하는 첫 번째 방법으로는 n개의 dimension 에 대해 각각 policy gradient를 구하는 방법이며 noisy, inefficient 하다는 단점이 있다.

Monte-Carlo policy Gradient
-
이를 하기 위한 여러가지 빌드업 중 하나로 likelihood ratio와 score function 개념의 소개

-
softmax policy를 취한다고 할 때 확률은 아래와 같이 정의됨
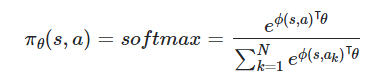
앞서 등장한 개념인 score function 값을 구하면 아래의 결과와 같은데 유도과정은 해당 링크에 설명되어 있음
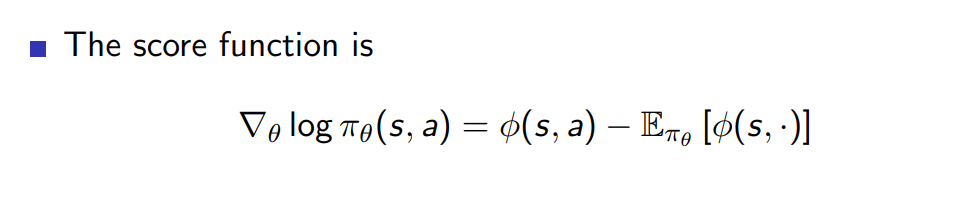
https://math.stackexchange.com/questions/2013050/log-of-softmax-function-derivative -
gaussian policy를 취할 때 확률은 아래와 같이 정의된다

이 함수에서 score function의 유도과정은 비교적 간단하다
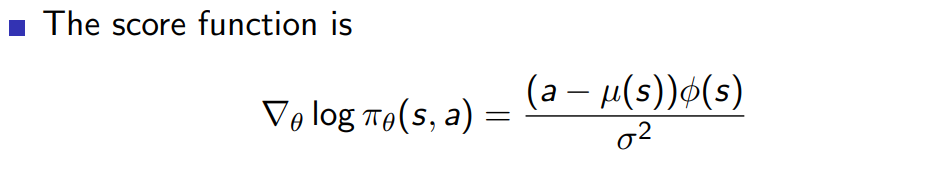
-
one-step MDP로부터의 확장
one-step에서는 instant return을 받기 때문에 아래와 같은 수식 전개가 가능하다.

-
위의 개념을 multi-step으로 옮기면 r이라는 instant return이 아닌 long-term value Q로 대체할 수 있으며 앞서 소개한 세 가지 objective function J에 대해 모두 다음과 같은 policy gradient를 보인다.

-
위의 개념들을 통해 얻은 최종적인 MC policy gradient 방식은 아래의 pseudo code와 같으며 의 unbiased sample 를 가정한다.
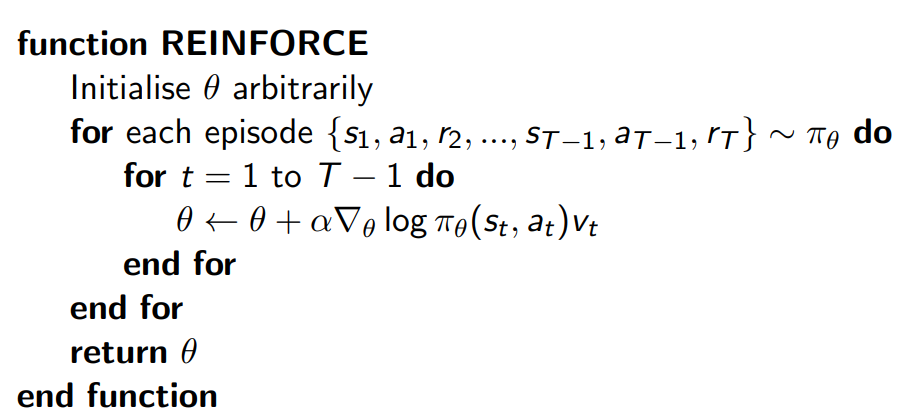
Actor - critic Policy Gradient
-
MC 방식은 아직 큰 variance를 갖는다는 문제가 있으므로 아래와 같은 알고리즘을 소개한다. Action value function Q의 function approximation을 하는 parameter w와 policy 를 업데이트 하는데 사용되는 parameter 가 있다. 이를 각각은 critic 와 actor로 불리며 approximate policy gradient를 수행한다

-
critic이 담당하는 일은 이전 장들에서 배운 policy evalution 문제와 동일하다(현재 policy에 대한 평가)
그리고 이런 문제를 해결하는데 MC, TD, TD() 등의 방식이 제시되었다. + LS(Least Squares) -
critic 이 variance를 줄이는 원리는 아래의 링크에 설명되어 있다.
https://www.quora.com/Why-can-a-critic-function-reduce-variance-in-the-policy-gradient-method -
아래는 Q function의 function approximation이 linear 하게 되어있을 경우를 가정하고 actor의 update 방식이 이 단원의 앞에서 배운 policy gradient 형식으로 update 된다고 가정했을 때의 pseudo-code 이다.

-
위의 방식은 (function approximated Q function)policy gradient를 approximate하고 있기 때문에 bias를 갖고 있다. 이는 맞는 solution을 찾을 수 없다는 문제를 야기할 수 있지만 적절한 value function approximation을 통해 이 bias를 제거할 수 있다.
Compatible Function Approximation Theorem
-
앞서 얘기한 적절한 value function approximation은 아래와 같은 두 조건을 만족할 때 이뤄진다.

-
두 번째 조건은 에 대해 더 이상 w에 대한 gradient가 없을 때 만족되며 이로부터 출발한 식에서
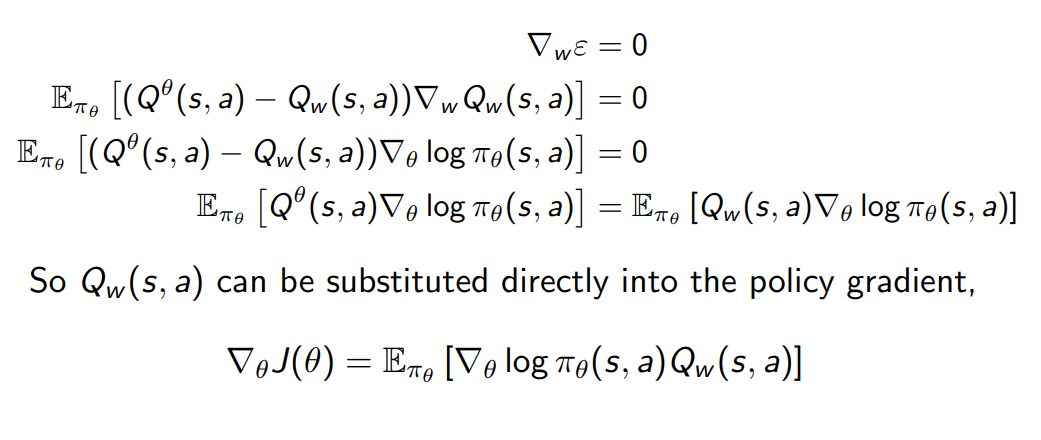
가 를 대체할 수 있음이 보여진다.
Action-Critic 방식을 개선하는 방법
- 아래의 식과 같이 expectation은 그대로 유지하면서 score function에 state에 관한 어떤 식을 곱한 형태를 빼거나 더해 변형할 수 있다.
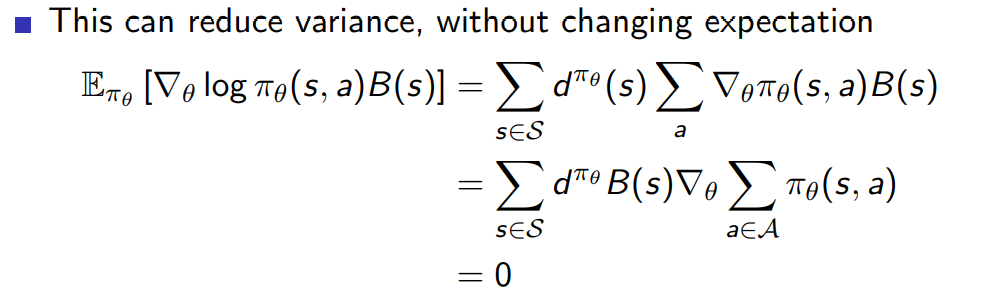
첫 번째 줄에서 뒤에 오는 policy 확률함수에서 log 가 빠진 것은 다시 생각해 봐야 한다.!!!
(2022.03.04)
expectation 구할 때 가 곱해지므로 log 의 gradient 분모의 것과 약분되는 과정생각해야 함
마지막 줄에서 0 이 나오는 이유는 모든 가능한 action에 대해 sum을 한 결과는 1이고 상수에 gradient를 취하면 0이 나오기 때문이다.
- 이런 성질을 응용하여 variance를 줄일 수 있는데 Q-V를 한 advantage function을 정의하여 사용한다. 이는 이번 action 이 갖는 value에서 평소 V (state s에서 general 한 value)를 뺀 값으로 variance 를 의미한다고 볼 수 있다.

그러므로 아래와 같은 최종적인 policy gradient 값으로 계산하게 된다.
Advantage function Estimation
-
Advantage function의 도입으로 critic은 advantage function을 예측하는 것이 목표가 되었으며 V, Q에 대해 function approximator를 도입해 각각 v,w parameter 알아내는 것을 목표로 한다.
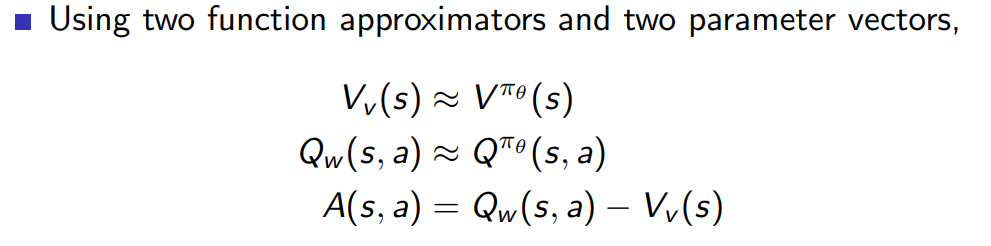
-
위와 같이 두 개의 parameter를 통해 각각 estimate 하는 방식 대신 적당한 근사를 통해 하나의 parameter 만으로도 policy gradient를 계산할 수 있다.
먼저 true value function에 대해 전개하면 아래와 같은 TD error에 estimate 값을 취하면 advantage function을 얻을 수 있음을 확인가능하다.

앞서 Advantage function 자리를 TD error로 대체할 수 있으므로 위와 같은 방식이 가능함을 알 수 있다.
실전에서는 true value function 가 주어지지 않았으므로 아래와 같이 function estimate 해서 TD error를 대체할 수 있다.
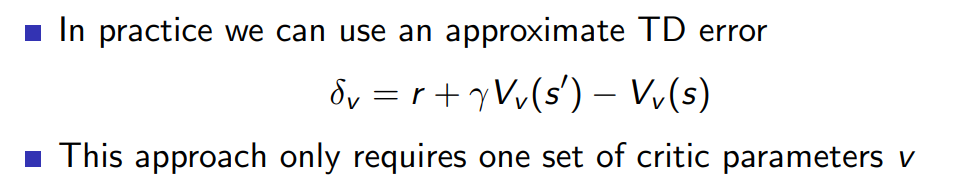
이는 앞서 소개한 v,w 두 가지 parameter를 쓰는 방식보다 유리하다
Actor and Critic in different time scales
-
critic의 역할은 action value function의 parameter를 업데이트 하는 것 (policy evaluation) 인데 이에 대한 target은 시간에 따라 변할 수 있으며 세 가지 알고리즘에 의해 다음과 같이 설정된다.

-
Actor 의 경우 앞서 배운 advantage function 말고 이미 친숙한 MC, TD, TD()등을 통해 target 설정 가능하다
-
Actor의 역할은 critic에 의해 제시된 방향으로 policy parameter를 업데이트 하는 것이며 위와 비슷하게 Monte-Carlo policy gradient 와 Actor-critic policy gradient 방식을 target으로 삼을 수 있다.

마찬가지로 TD() 방법으로 different time scale의 reward 들을 사용할 경우에는 forward와 eligibility trace를 사용한 backward가 비슷한 방식으로 가능하다.


Natural policy gradient
- 위에서 제시된 방향이 아닌 다른 방향으로도 더 효율적인 gradient update가 가능한데 이 부분은 더 찾아 공부해 보도록 한다.
Summary
- policy gradient은 actor 담당, policy evaluation은 critic 담당이므로 아래와 같이 이번 chapter에서 배운 내용을 정리할 수 있다.

