5. Value Function Approximation

이두현·2022년 2월 20일

ReinforcementLearning

Value Function Appproximation 개념

이전까지 우리가 value, action-value function 값을 불러온 방식은 각각 s와 (s,a)를 entry로 하는 lookup table 방식이었다.
하지만 큰 model에 대해서는 각 state에 대해 value를 배우는 것이 너무 느리고 모든 정보를 저장하는 것이 단점으로 작용하므로 아래와 같이 parameter를 추가하여 함수를 근사하는 방식을 생각하게 되었다.
$\hat{v}(s,w)\sim v_\pi(s) \\ \hat{q}(s,a,w)\sim q_\pi(s,a)$
이 파라미터 w는 향후 MC나 TD 방식으로 update 될 수 있다
아래 그림과 같은 미지의 box를 생각해 볼 수 있으며 가운데와 같이 유도되는 함수 형태를 action-in 이라 하며 오른쪽은 action-out 이라 부른다.
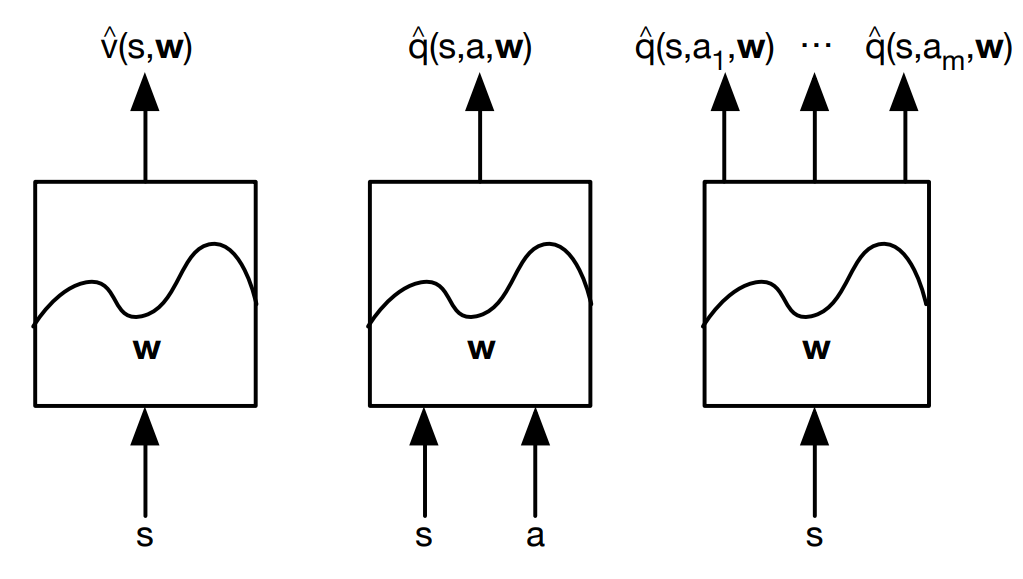
function approximator 는 linear combination 을 사용하거나 Neural Network를 사용한다

Gradient Descent Recap

벡터 w를 parameter로 갖는 J 함수에 대해 gradient를 계산하면 아래와 같다.

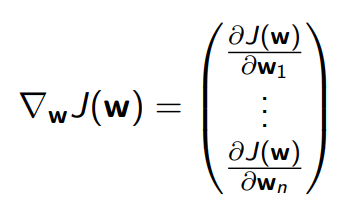
local miminum을 찾기 위해 우리는 아래와 같이 벡터 w를 update 하며 alpha는 step-size paratmer 이며 음수 부호와 1/2는 계산의 편리함을 위해 추가되었다.
$\Delta w=-\frac{1}{2}\alpha\nabla_wJ(w)$

Value function and SGD

우리의 objective function은 실제 value function을 의미하는 $v_\pi$ 와 approximation fuction인 $\hat{v}(s,w)$ 의 차이를 최소화 하는 것이며 강의에서는 실제 value function은 일단은 Oracle에 의해 주어진다고 가정하고 설명한다.
앞서 벡터 w에 대한 함수가 주어진 경우 local miminum을 찾기 위해 w에 가해야 하는 변화량을 계산했는데 이를 참고하면 아래와 같은 결론을 얻는다.

Feature vector & Linear value Function Approximation

state를 나타내는 형태이며 다음과 같이 벡터로 표현되어 value function은 linear combination으로 state의 요소에 weight를 가해 표현가능하다
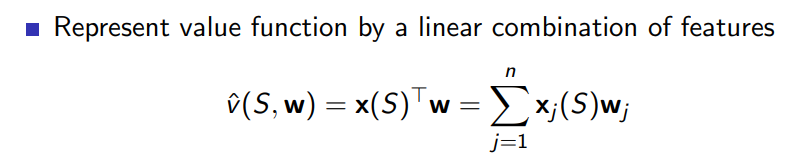
앞선 절에서 본 벡터 w에 대한 변화량 식에서 $\nabla_w\hat{v}(S,w)$ 에 해당하는 자리에 $x(s)$ 가 들어가야 하므로(v는 x와 w의 단순내적) update rule은 아래와 같다.

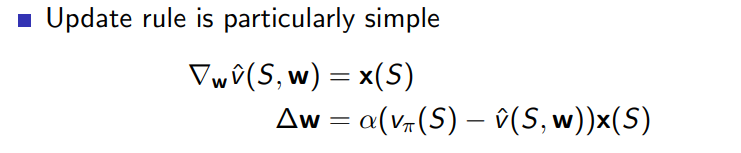
Incremental prediction algorithms

위에서 제시한 update rule은 true value function인 $v_\pi$ 가 주어져 있었지만 실제 상황에서는 그렇지 않으므로 이를 subtitute 할 세 가지 alternative algorithm이 제시되었고 각각은 아래와 같다

Recap and algorithm details

MC 방식은 target 함수로 $G_t$ 를 사용하기 때문에 unbiased, noisy sample(high variance) 성질을 갖는다.

Local optimum에 수렴한다고 하며 위에 제시된 것과 다르게 non-linear function에서도 작동한다.

TD 방식은 bootstrapping 방식을 사용하기 때문에 biased 된 sample이며 global optimum에 가까이 수렴한다고 한다.
TD( $\lambda$ ) 방식은 마찬가지로 biased 되어 있으며 앞서 배운 대로 eligibility trace 함수를 이용하면 backward와 forward view 가 아래와 같이 동일하게 적용될 수 있다.

Value function control 과 Action-value function approximation

policy control 과정에서 improvement는 앞선 chapter에서 배운 것과 같이 $\epsilon$ -greedy 방식으로 진화한다는 점에서 동일하지만 evaluation은 approximate policy evaluation을 하게 되고 뒤이서 설명하도록 하겠다
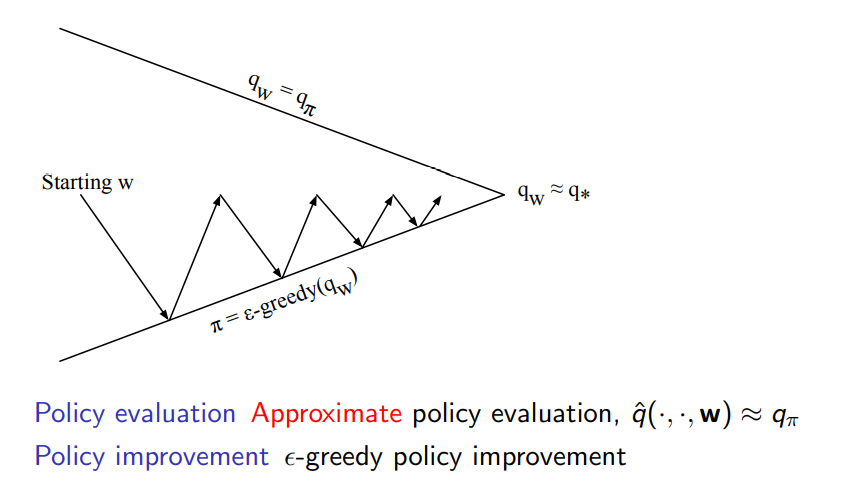
Action value function도 state value function 과 마찬가지로 parameter w를 추가해 s,a,w 를 갖게 되며 true action value function $q_\pi$ 를 갖는다고 했을 때 다음과 같이 parameter w를 업데이트 할 수 있다.
앞서 state value function에서 했던 것과 마찬가지로 feature에 대해 아래와 같이 linear combination으로 나타내면 state value function q에 대해 gradient를 구했을 때 state feature vector 만 남게 되므로 아래와 같은 parameter 업데이트 결과를 얻는다
앞서 말한 true action value function $q_\pi$ 가 실전에서는 주어지지 않기 때문에 state value function에서 했던 것과 같이 세 가지 방식으로 target 함수를 잡고 parameter update 할 수 있다.

Convergence

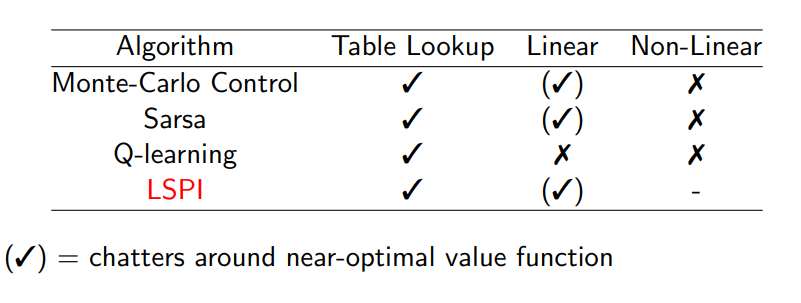
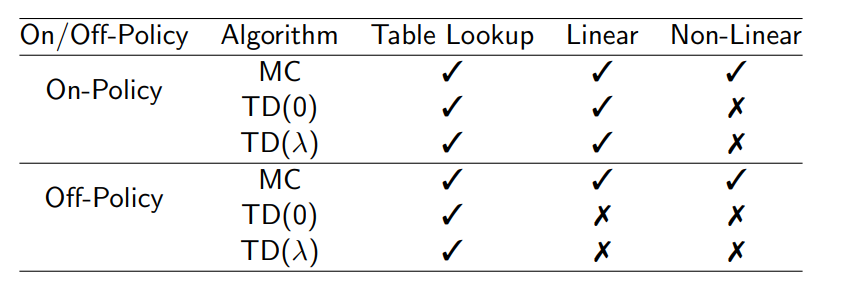
도표에서 table look-up은 v에 대해서는 (s), q에 대해서는 (s,a)와 같이 모든 entry에 대해 값이 정해져 있었는데 이러한 방식을 의미한다
Linear은 위에서 계속 사용한 state의 feature vector와 linear combination 하는 방식을 의미하며 non-linear는 Neural Network를 통해 additional parameter w를 배우는 방식을 의미한다.
On/Off policy는 앞장에서 배운 것처럼 현재 배움의 재료로 쓰이는 policy가 update 하고자 하는 직접적인 목표인지 서로 다른지에 따라 좌우됨을 의미한다.

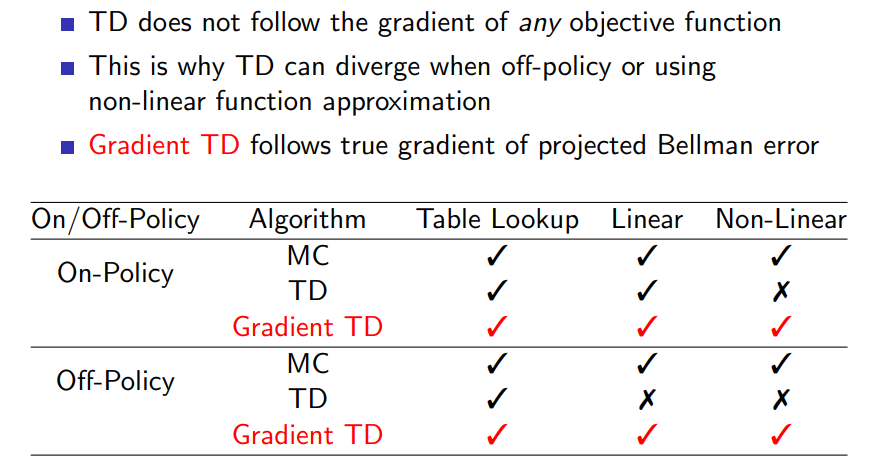
Gradient TD는 TD의 divergence를 보완하기 위해 개발된 방법이며 이와 관련해서는 더 공부를 해보도록 하자

Batch Method

(state,value) 를 묶어 batch로 여기며 이를 training 재료로 사용하는 방식을 의미한다.

Least squares Prediction and SGD

D 와 같은 batch가 있을 때 각 time step에 대해 target 값 $v_t^\pi$ 에 가까워지게 Least square를 구하는 방식을 소개한다.
이런 방식을 소개하는 이유는 batch에서 (state,value)를 sample 하여 위에서 배운 SGD를 적용하면 Least Square 의 해에 수렴하기 때문이다

DQN (Deep Q-Networks)

기존 방식에는 두가지 문제가 존재했다

deep learning 으로 RL을 학습하는 과정에서 label이 될 만한 것은 Reward 뿐이였기 때문에 학습에 어려움이 있다.
deep learning의 data sample은 iid를 가정하지만 RL 학습에서는 state 간 correlation이 크기 때문에 이 가정이 성립하지 않는다.
하지만 ( $s_t,a_t,r_{t+1},s_{t+1}$ ) 시퀀스 자체를 저장하여 이를 학습의 재료로 사용하는 experience replay 방식을 사용하고 이러한 메모리에서 위의 정보를 임의로 추출하여 iid를 가정하는 deep learning에 맞는 학습이 이뤄질 수 있도록 하였다.

fixed Q-target이라는 개념은 Q 함수가 타켓으로 하는 함수에는 old parameter를 사용하는 방식을 의미하며 이는 TD에서 update가 될 때마다 target 함수가 변하는 문제를 보완하는 성격을 갖는다. 세부적인 내용은 향 후 논문을 통해 자세히 공부해 보도록 하자.

experience replay
stable compare to naive - because decorelated trajectories

fixed Q-targets
Q 가 target으로 하는 함수에는 old parameter를 사용하고
(stable update; TD 에서 문제가 되는 한번 업데이트 시 target이 변하는 문제를 보완하기 위해)

Linear value function approximation 시 바로 계산

앞서 했던 것처럼 value function을 $\hat{v}(s,w)=x(s)^T w$ 로 두었을 때 SGD 방식으로 도달하는 Least square의 minimum에서는 parameter w에 대한 gradient 변화가 더 이상 없어야 하며 기대값으로 아래와 같이 표현할 수 있다. 또한 parameter update에 관한 수식을 통해 w에 대한 식을 한번에 계산하기 위해서는 아래와 같이 계산하면 된다.

이제 state 개수가 아닌 feature vector의 dimension에 비례하는 시간 복잡도를 확인할 수 있다.
앞서 제시했던 MC, TD, TD( $\lambda$ )에 대해 target function $v_t^\pi$ 는 모두 다르기 때문에 각각의 식은 아래와 같이 나타나며 LS 접두사는 Least Square를 의미한다.
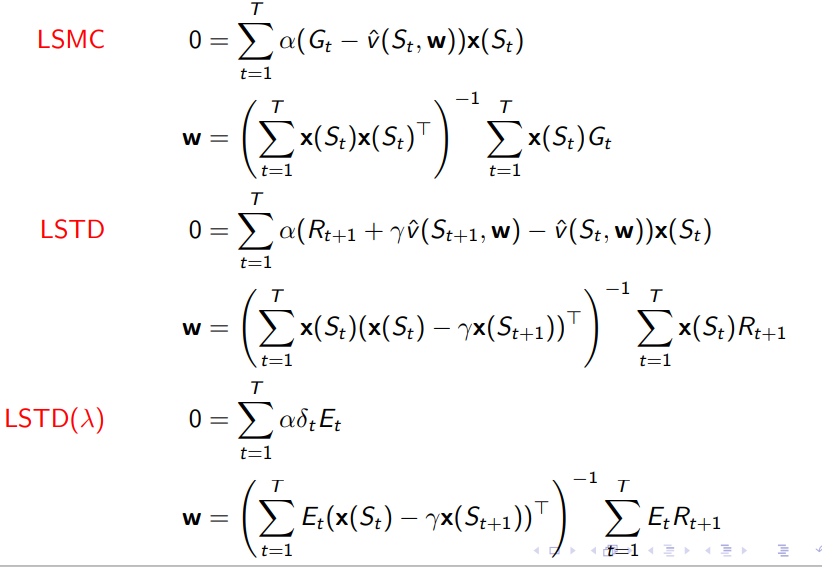
각각의 방식에 대한 convergence 결과를 통해 어떤 알고리즘을 사용해야 하는지 알 수 있다.

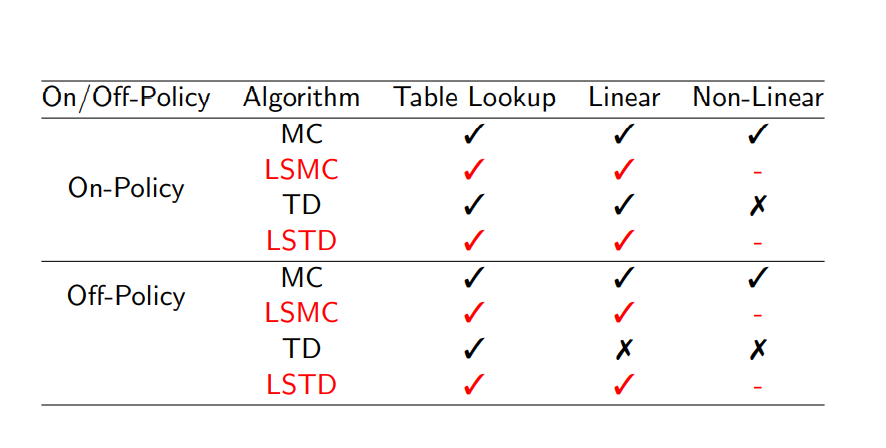
Least squares Control (policy iteration)

앞장에서 배운 Q-learning에 LS(least squares)를 접목해서 policy iteration을 구성할 수 있다.
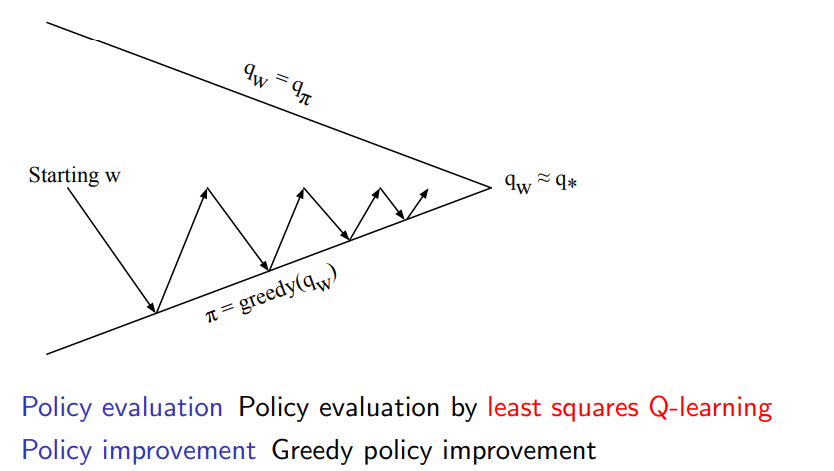
Training 자료로 쓸 Experience 들이 서로다른 policy에서 generate 되었기 때문에 off-policy learning의 일종인 Q-learning을 사용하는 것이고 아래와 같은 아이디어를 사용한다.
앞에 했던 것과 마찬가지로 LS(Least squares) minimum은 더 이상 parameter 변화가 없음을 의미하므로 off-policy 수식을 살짝 변형해서 ( $\gamma\hat{q}(S_{t+1},\pi_{new}(S_{t+1}))$ 이 아닌 $\gamma\hat{q}(S_{t+1},\pi(S_{t+1}))$ ) matrix mult 형태로 변형하면 다음과 같다.

이 방식은 LSTDQ 라고 부르기로 한다.
LSTDQ를 이용한 Least Squares Policy Iteration의 pseudo code은 아래와 같다.