기존 single Agent RL의 한계
- multi-agent system에서 action space가 joint 되면 agent 수에 따라 exp하게 증가하므로 기존 방식으로 parameterised 하여 표현할 수 없음
- 또한 partial observability와 communication 해야 할 수 밖에 없는 상황이 이러한 framework 발전을 필요하게 만든다.
아직 해결되지 않은 문제점
-
현재 중론은 centralised training of decentralised policy 인데 centralised learning의 이점을 최대한 이끌어낼 방법에 대한 연구는 이뤄지지 않았다.
('how best to exploit the opportunity for centralised learning remains open') -
joint action 끼리 상호작용 이후 관찰할 수 있는 것은 global 한 return인데 이 정보만으로는 각각의 agent의 기여를 알기 힘들다는 것이 문제점이다. (indiviual reward 설정 방식은 한계를 갖는다.)
참고) COMA는 actor-critic 방식에 기반하고 있음
Recap Actor-Critic
- critic의 역할 : action value function 의 paratmeter w 로 function approximation 된 상태에서 w를 업데이트 한다.

- Actor의 역할 : policy gradient에서 배운 방식으로 policy update를 하며 parameter를 변화시킨다.
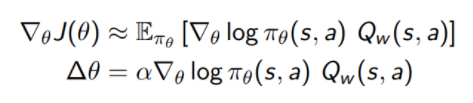
COMA 방식의 세가지 아이디어
- centralised critic 사용
- critic은 learning에만 사용되고 actor는 execution에 사용된다는 점에서 learning 과정에서 모든 joint action을 조절하는 centralised critic을 사용한다는 의미
- counterfactual baseline 아이디어
-
difference reward(agent가 현재 action으로 얻은 reward와 default action을 수행했을 때 얻는 global reward를 비교하는 방식) 에서 영감을 얻음
-
위 방식의 한계는 default action 선정 방식의 모호함에 있다
-
centralised critic은 current joint action 의 예측값과 counterfactual baseline을 비교하는 함수인 advantage functino을 각 agent 에 대해 계산하게 된다.
- critic representation 아이디어 사용
- 아직 잘 이해안됨 향 후 읽어보고 작성
Related Work
- 이 논문과 가장 가까운 방식으로는 Foerster et al.(2017) 마찬가지로 decentralised policy와 multi-agent representation을 사용하지만 DQN을 사용하면서 experience replay를 안정화 시키는데 최선을 다한다. 하지만 이는 centralised training regime을 온전히 모두 사용하지 못한다는 단점을 갖고 있다.
Background
-
Agent 를 a로 표현하기 위해 action을 U로 표기하여 사용
-
O(s,a)는 partially observable 한 환경 함수를 나타내며 이를 통해 얻은 element는 집합 Z 에 속한다.
-
single agent policy gradient 방식에 대하 recap
목적함수는 이며 이를 최대화 하기 위해 에 대해 gradient ascend 전략을 취하게 된다. 이 방식을 통해 취해야 하는 gradient는 다음과 같다.
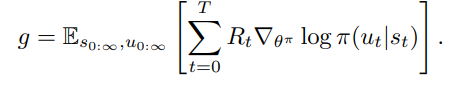
임을 참고하자
Silver 강의 6장에서 위의 는 action value Q(s,a)로 치환될 수 있고 가 Expectation 값에 영향을 주지 않음을 수식적으로 증명할 수 있으므로 variance를 줄이기 위해 Advantage function 를 도입하는 방식도 소개된 적 있다. -
이 논문에서는 policy evalutation을 담당하는 critic의 target function으로 를 취하고 있다.
loss function은 아래와 같이 target 값과 function approximation을 통해 얻은 값의 차이에 대한 L2 값이며 이를 최소화 하는 방향으로 gradient descent 한다.
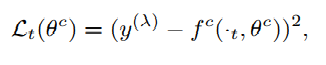 (강의에서 critic function approximation의 parameter는 흔히 w로 표현하였었다.)
(강의에서 critic function approximation의 parameter는 흔히 w로 표현하였었다.)
target value y는 아래와 같은 식으로 표현되며 이 n-step은 target network로부터 bootstrapping 되었음을 참고하자.
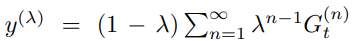
본론
IAC(Independent Actor-Critic)
-
기존의 방식으로 각 agent가 각각의 actor와 critic을 학습시키는 방식사용
-
나중에 결과를 비교하기 위해 저자가 구현한 IAC의 방향은 agent 간 parameter를 공유하는 방식이며 이는 한개의 critic과 actor로 모든 agent들이 학습됨을 의미한다.
-
이러한 방식이 가능한 이유는 각 agent들이 다른 결과를 observe하며 이에 따른 각각 다른 hidden state를 구성할 수 있기 때문이다.
-
필자가 implement한 IAC-V 는 critic이 value function을 esimtate 하는 방법이며 target은 TD error를 기준으로 SGD 한다.
-
IAC-Q는 critic이 action value function을 estimate 하는 방법이며 advantage function 을 기준으로 SGD 한다.
-
위 방식들의 단점은 trainig time 에서 agent간 공유된 information 부족으로 coordinated 전략을 짜기 힘들다는 점과 각 agent가 total reward에서 자신의 기여도를 알아채기 어렵다는 점이다.
COMA (Counterfactual Multi-Agent Policy Gradients)
-
위의 문제를 제거하기 위해 centralised 된 한개의 critic을 사용하고 각 agent에 대한 actor가 존재하므로 전체적인 diagram은 아래와 같다.
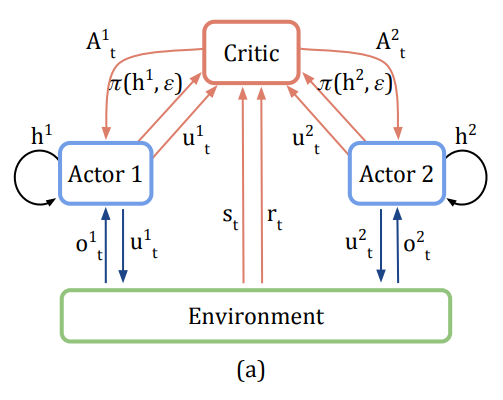
-
counterfactual baseline을 사용하게 된 이유
central critic에서 얻어진 Q(혹은 V)에 대해 TD error 기반 gradient ascend를 하면 식은 아래와 같다.
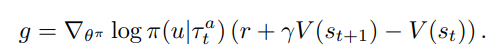
하지만 이 방식의 단점은 위에서 보다시피 Global reward에 대한 고려만 하다보니 각 agent입장에서는 자신이 얼마나 기여를 하고 있는지 모른다는 점이다.
또한 다른 agent들도 explore를 진행하기 때문에 gradient이 매우 nosiy 해 질 것이다. -
이러한 문제제기를 통해 나온 두 번째 개념이 (difference reward)를 사용하는 것이며 global reward 개념이 아닌 아래와 같은 방식을 사용한다.

표기는 이 함수의 기준이 되는 agent a를 제외한 다른 agent들의 action 집합을 의미하며 는 default action을 의미한다.
하지만 이 방식에서도 default action을 알기 위해 simulator를 소유해야 한다거나 각 과제에 대한 user-specified default action을 정해야 한다는 단점 혹은 모호함이 남아있다. -
이러한 문제점을 해결할 수 있음과 동시에 각 agent에 대해 서로 다른 reward function을 제공할 수 있는 방법은 아래와 같다. (counterfactual baseline 등장)

A는 counterfactual advantage, RHS의 두번째 항은 counterfactual baseline을 의미
도표에서 본 것 같이 한개의 critic이 생성해낸 joint action에 대한 Q value를 기준으로 어떤 action u를 취했을 때 자신을 제외한 다른 agent들이 가질 Q 값의 stochastic 한 평균을 뺀 advantage function의 형태로 나타낸다.
() 임을 기억해 직관적으로 이해해 볼 수 있음
counterfacutal baseline 이 다른 policy와 joint 되어 gradient에 영향을 미칠 확률이 없기 때문에 self-consistency 문제에서도 이 방식은 자유롭다 라고 기술되어 있음 -
DQN에서와 비슷하게(내 생각에) 이를 DNN을 통해 학습하려고 할 때 action space에 대한 dimension 이 계산 복잡도에 영향을 주는데 이 논문은 critic representation 이라는 방식으로 이를 극복한다.
-
다른 agent 들의 action 집합 자체를 네트워크의 input으로 집어넣어 output으로는 각 action 에 대한 Q value들만 나오게 설정하여 dimension 의 저주를 제거한다. (single forward pass 만으로 counterfactual advantage가 계산가능해진다)
-
(b)와 (c)는 각각 actor와 critic을 나타내며 actor가 RNN 같은 시계열 처리 구조를 통해 update 된다?
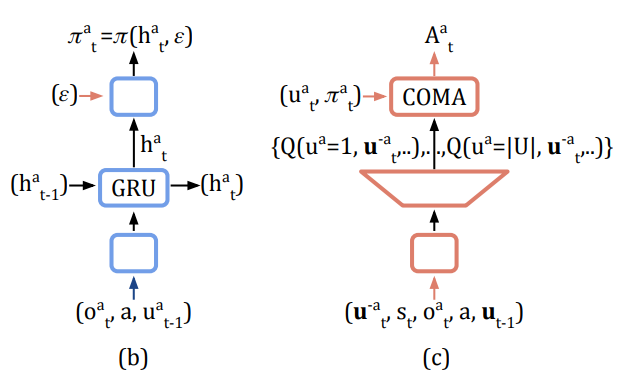
COMA가 local optimum으로 수렴함을 증명
-
과정은 이미 actor-critic 방식이 local maximum에 도달할 수 있음이 증명되어 있고 multi-agent 문제를 기존의 actor-critic 문제로 변환할 수 있음을 보이는 식으로 증명된다.
-
아래와 같은 graident와 advantage 함수가 주어졌을 때 우리는 (Silver) 강의를 통해 b(s) 가 expectation, 즉 gradient에는 영향을 주지 않음을 알 수 있다. - expectation은 그대로 두고 variance만 줄여주는 효과
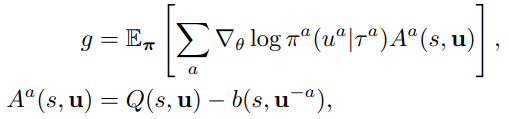
-
그러므로 gradient에 영향을 주는 것은 Q 함수만이고 아래와 같이 변환하여 총체적으로는 원래의 actor-critic gradient 변화의 모습으로 동치시킬 수 있다.
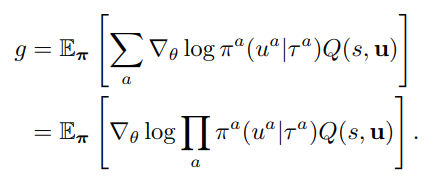
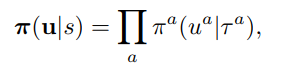
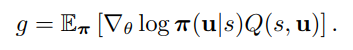
정리
actor가 LSTM 혹은 GRU 를 통해 구성되어 있는 점은 나중에 코드를 통해 공부해 봐야 할 것 같다.
Multi-agent RL에 대한 논문 reading list 는 이 분의 블로그를 참고하고 있다.
https://m.blog.naver.com/jk96491/222018882435
감사합니다...
