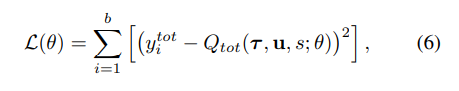state 가 hypernetwork 지나는 이유
Q1 ~ Qn 에 대해 monotonic 하게 Q_tot 가 비례하는 것은 맞으므로 W 원소들이 양수인 것은 맞지만
state가 이 과정에 관여하는 과정에서는 monotonic 할 필요는 없으므로 hyperparameter를 통과하여 자율성을 증가시킨다.
그리고 state가 direct하게 mixing network에 섞이지 않는 이유는 state 정보가 non-monotonic 하게 Q_tot에 extra state information 을 제공할 이유가 있기 때문이다.
Background
기본적인 notation은 앞선 COMA 논문과 모두 동일함
앞서 등장했던 여러가지 RL 학습 방법에 대한 간략한 소개
-
DQN
replay memory 와 아래와 같은 loss function을 최소화 하는 것을 목표로하는 학습 방식을 의미한다.
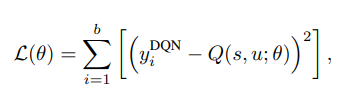
target 함수 는 TD(0) 값으로 아래와 같은 estimation을 가지면 는 한 batch에 대해 계속 같은 parameter로 목표값을 제시하는 target network 를 의미한다. (이 network는 한 batch iteration 이후 parameter update를 진행하게 된다.)
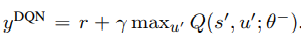
-
DRQN - Deep Recurrent Q Learning
critic-actor 방식에서 actor에 대해 LSTM이나 GRU 같은 시계열 처리 network를 적용한 방식을 의미한다.
향 후 졸업논문을 위해 이 논문도 살펴봐야 할 것 같음 -
Independent Q-Learning
mutli-agent Learning의 한 종류이며 주어진 task를 single-agent 문제로 분해한 후 합친 방식으로 생각하는 framework를 제안하였다.
이 방식의 문제점은 한 agent가 학습을 할 때 다른 agent들의 policy가 바뀐다는 점을 간과해 non-stationarity 성질의 등장으로 수렴성을 보장받을 수 없다는 점이다.
복습을 위해 => COMA 방식에서는 Q value target 설정 시 다른 agent들의 action 집합을 고정시킨 채로 학습을 진행한다.!! -
VDN - Value Decomposition Networks
위와는 정반대로 joint action value function 을 구하는 것을 목표로 하는 framework를 갖고 있다.
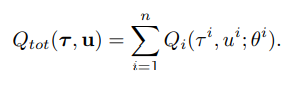
각 agent의 Q 값의 합으로 전체 action-value function을 포함한다.
하지만 주의할 점은 가 i 번째 agent의 expected return을 보장하지는 않으므로 action-value function보다는 utility function으로 이해하는 것이 맞다고 한다.
QMIX
논문에서 제시한 이 방식은 앞서 소개한 IQL 와 VDN의 중간 (Q function 기준으로 완벽한 분해 <-> 완벽한 결합) 방식을 추구한다.
VDN에서는 아래와 같은 식을 만족하면 consistency가 만족된다는 주장을 펼친다.
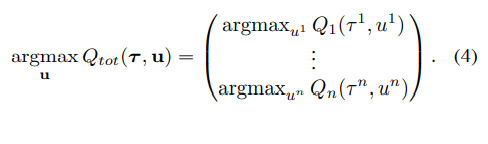
수식에 대한 설명은 전체 jointed Q-function 의 action에 대한 argmax 결과 벡터가 각 agent에 대한 Q function의 개별적인 argmax 결과의 종합과 동일하면 된다는 의미
- 이 방식은 off-policy learning method에서 구해야 하는 에 대한 값을 각 agent Q-function으로부터 쉽게 구할 수 있다는 부수적인 효과를 갖는다.
VDN 방식은 위의 식(4)를 만족하기 충분하지만 QMIX 논문은 이러한 조건은 더 큰 범위에서 monotonic function (단조 함수) 로서 표현이 가능하며 그러한 monotonicity는 아래와 같은 와 관계가 성립할 경우 보존된다는 점을 강조하고 있다.
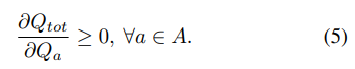
위 식의 직관적 이해는 각 agent의 expected return을 증가시키는 방향으로의 변화는 overall expected return을 증가시키는 방향과 동일하다는 식으로 가능하다. (앞선 VDN에서 는 여러 agent들의 Q-function 값들의 합으로 표현되었었다는 점을 기억하자)
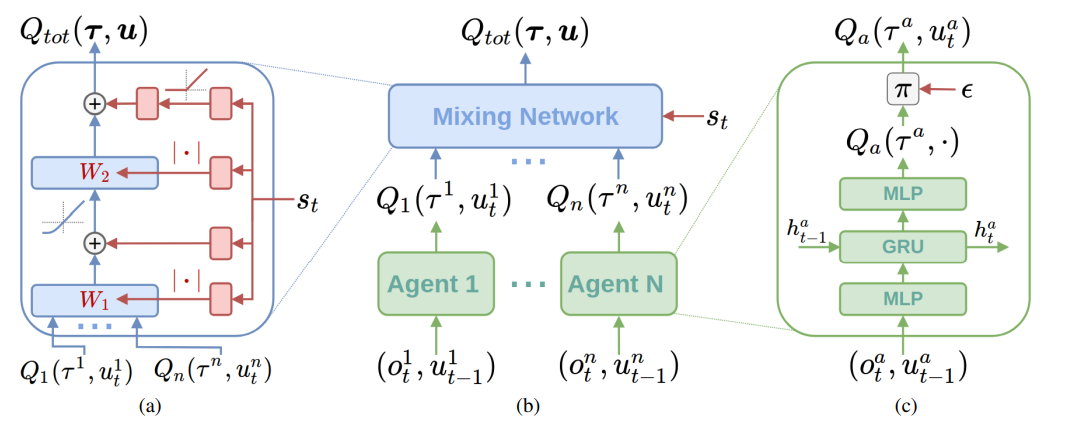
QMIX architecture
아래 그림은 QMIX의 전체적인 구조에 대해 설명하고 있다
-
먼저 각 agent들은 DRQN 형식을 띄어 과거에 취했던 action 집합에 대한 학습이 가능하다. (향 후 DRQN 방식에 대한 학습이 필요할 것으로 보임)
-
위의 절에서 식(5)를 소개하며 monotonicity를 유지해야 한다고 강조했는데 이러한 수식은 mixing network의 weight들을 양수로 제한하는 방식으로 구현될 것이다. (Q 값들에 양수 weight + non-linearity로 최종적인 Q total 값이 결정된다.)
논문에서는 bias에 대해서는 이러한 restriction을 걸지 않는다고 설명하고 있다. -
위의 non-negative 한 weight들은 각각 분리된 hypernetwork를 통해 구해진다. 이는 각각 single layer와 absolute activation function의 합으로 구성되어 있으며 (음수 결과를 내지 않기 위해) 위의 그림 (a)를 통해 확인가능하다.
-
여기서 state를 바로 mixing network에 대입하지 않고 weight의 형태로 (이를 generate하는 재료로) 사용하는 이유는 에 non-monotonic 한 방식으로 extra state information을 주기 위함이다. (이로써 더욱 다양한 state representation에 대해 학습 가능)
-
최종적인 손실함수는 DQN과 비슷하게 아래와 같은 식을 사용하며 batch 훈련이 진행되는 동안에는 freeze되어 있는 target network의 parameter를 사용한다는 점도 비슷하다.