DFAC : Factorizing the Value Function

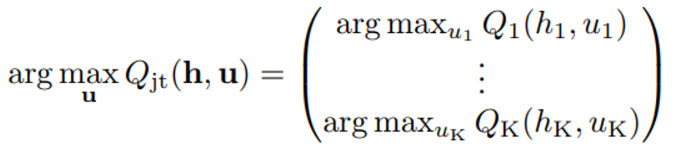
Intro

CTDE framework의 등장 배경

1) Agent들의 behaviour change로 인한 env의 불안정성

2) Other agent action에 의한 가짜 reward로 인한 학습 불안정성

을 타파하기 위해 training은 안정화 시키고, 각 agent의 decentralized execution 능력은 최대로 하기 위한 방안

Value function factorization 방식

가정)

1) 각 agent의 optimal action 의 joint는 전체 optimal joint action을 형성한다.

2) 전체 return 은 각 agent의 utility function으로 분해할 수 있다.

한계)

utility 의 expectation을 구하는데 초점을 맞추다보니 전체 return이 갖고 있는 additional 정보를 잃어버리게 된다.

예) VDN, QMIX 등

Distributional RL과 Value function factorization 방식과 비교해 한계

방식)

한개의 single Q value를 scalar 형태로 return하는 것이 아닌 return의 probability distribution을 반환한다.

Value function factorization을 이길 수 없는 이유)

1) individual global max(각 agent 의 optimal의 모임이 전체의 optimal…) 이 distributional 하게 유지되어야 함

2) 전체 return의 probability distribution을 factorization 하는 방식

• 하지만 이 방식은 전체 reward가 갖고 있는 additional information을 뽑아낼 수 있는 potential을 갖고 있음!

Intro

CTDE 등장 배경

1) 다른 agent 들에 의한 non-stationary env (policy 가 계속 변함)

2) spurious(가짜) reward signal

이중 value function factorization 이 큰 성공을 거둠

IGM(Individual Global Max) 아이디어에 기반

→ 각 agent 의 optimal action 집합은 optimal joint action과 동일하다

→ 이는 각 agent 개별의 분리된 utility function 의 존재를 가능하게 함

• 현재 알고리즘들이 이러한 utility function의 expectation에만 집중하고 있다는 점을 지적

지금까지 제시된 distributional RL 은 value function factorization과 잘 섞이지 않음

1) IGM을 distributional 형태로 유지하는 것

2) total return의 probability distribution을 individual utility로 factorize 하는 것

에서 오는 어려움으로 인해

이 둘을 섞을 수 있는 DFAC 알고리즘을 소개

1) Mean-shape decomposition → IGM을 깨지 않고 기존의 vlaue function factorization(VDN, QMIX)를 DFAC variant로 변형가능

2) Quantile Mixture → total return distribution을 individual utility distribution으로 나누는 역할

---

Background

S: global state, training 시에는 접근 가능하지만 execution에는 참고 불가

K: index of an agent

O: observation 집합

H: action-observation joint 집합

U: joint action 집합

이 논문에서는 stochastic policy를 다룸 // H를 conditional 로 갖는 policy로 인해 U가 결정됨

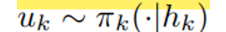
IGM 을 수식으로 나타내면 아래 수식과 같다

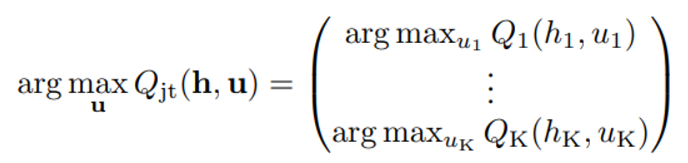
QMIX에서 봤던 가정 식과 동일하다!

→ 이 가정을 통해 각 agent의 utility function maximization 이 joint maximization과 동일하다는 결론을 얻을 수 있다.

Value function Factorization method 에는 우리가 봤던 VDN, QMIX가 있으며 각각의 수식은 아래와 같다

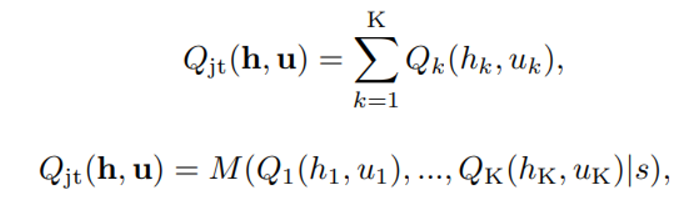
IQN recap

기존과의 차이점

Inverse quantile function의 정의역을 equidistance로 설정하지 않고 [0,1] uniform random sampling을 통해서 자유도를 놉혔다.

이렇게 선정된 goal (w) 들은 아래와 같은 함수를 통해 embedding 된 후 state 와 element-wise 하게 embedding 된다

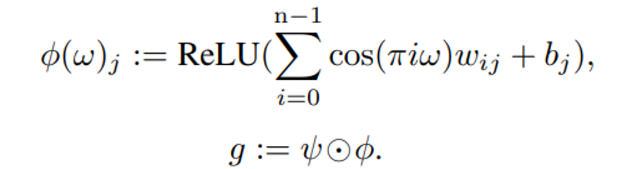
아래는 state embedding과 goal(w) embedding 의 element-wise interaction을 의미하며 결과값인 g는 quantile function의 결과값을 추정하는 역할을 한다.

전체 네트워크는 아래와 같은 loss function을 최소화하는 방향으로 학습되며

기존에 제시된 다른 distributional RL과 달리 expectation으로 Q-value 를 정하지 않고 random sampling을 통해 value function 값을 추정한다.

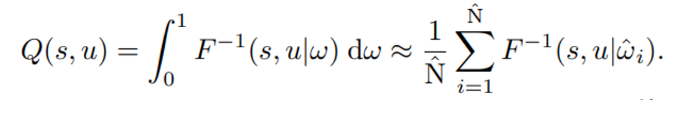
Network를 통한 quantile mixing 개념

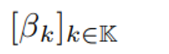
위의 값들이 model parameter 일 때

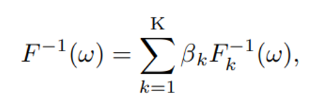
위와 같은 방식으로 여러 quantile 들의 합으로 새로운 quantile 을 묘사할 수 있다. 이 때 좌변이 quantile function 의 properties를 만족시켜야 한다는 제한사항이 존재한다

---

DFAC Methodology

우리는 다음과 distributional value function 이 아래와 같은 조건을 만족할 때 Distributioal IGM, 즉 DIGM 이 성립한다고 정의한다.

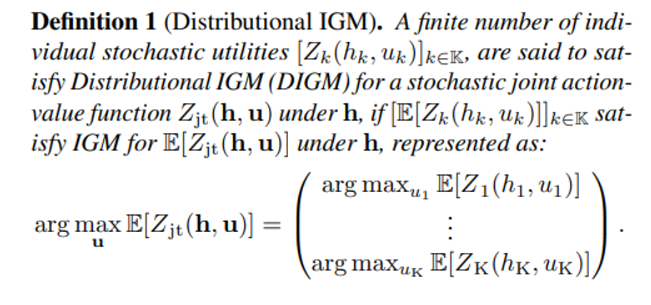
하지만 conventional 한 Q function 의 factorization function 으로는 distributional value function 의 DIGM 조건을 만족시키는 factorize 결과를 얻을 수 없다!

즉, $\Psi$ 가 Q를 IGM 조건을 만족시키며 factorize 할 수 있는 함수라 했을 때 이 함수를 똑같이 distributional value function Z에 적용하는 것은 Z가 DIGM 조건을 만족하기에 충분하지 않다는 것이다!
이에 대응해 DFAC에서는 mean-shape decomposition을 아래와 같이 제안한다.

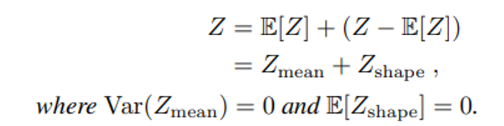
이를 통해 우리는 $Z_{mean}$이라는 deterministic 한(variance = 0) 항과 뒤의 $Z_{shape}$이라는 stochastic 한 항으로 Z를 분리할 수 있게 된다.

Definition 1에서 확인할 수 있듯이 DIGM 은 Z의 expectation 으로 이뤄져 있기 때문에 $Z_{mean}$에 대해서는 정확한 factorization이, $Z_{shape}$에 대해서는 rough 한 factorization 이 허용된다(expectation 이 0이므로)

위와 같은 직관을 통해 DIGM을 만족하기 위한 충분조건의 factorization을 아래와 같이 고려할 수 있다.

앞서 언급한 것과 같이 $\Psi$ 를 면밀하게 고르는 것이 IGM의 성립여부를 결정하며 phi 함수는 expectation 이 0인 이상 IGM 성립 여부에 큰 영향을 미치지 않는다.

(하지만 $\Psi$ 에 대한 것은 이미 VDN, QMIX 에서 본 것과 같이 conventional 한 Q-value function에 대한 factorization 으로부터 알 수 있다.)

그러므로 이어지는 내용에서 우리는 $\Phi$함수($Z_{shape}$과 연관)를 효과적으로 선정하는 방식에 대해 설명하도록 한다.

---

Theorem 3에서는 quantile function 이 다음과 같이 non-negative 한 model parameter를 통해 조합될 수 있다면 아래와 같이 quantile function 에 대응하는 Random Variable Z 가 존재한다고 한다.

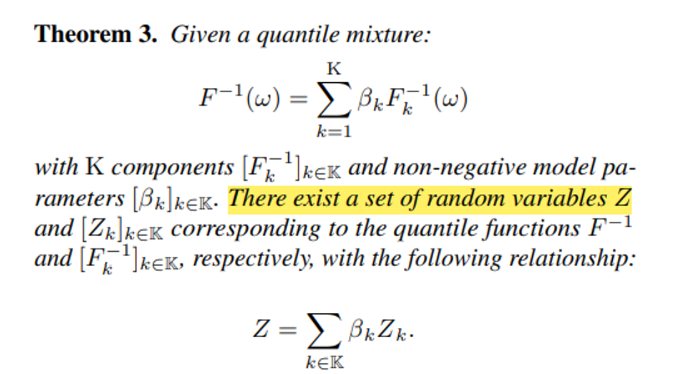
이는 IQN 모델을 사용하기 위한 응용이며 앞서 $Z_{shape}$은 $Z-E[Z]$로 표현되었기 때문에 아래와 같이 factorization 이 가능하다 (expectation Z가 Q에 대응하는 모양)

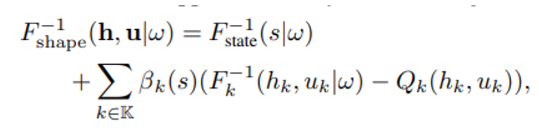
여기서 우변의 첫항인 $F_{state}^{-1}$은 QMIX 의 global state information 참고 항 같이 state info 를 training 과정에서 사용하기 위해 추가된 term으로 여겨진다.

위와 같은 과정을 통해 quantile function을 각 agent 의 individual utility 처럼 factorize 할 수 있게 되었으며 위의 내용은 여러 IQN 모듈의 종합으로 implement 되었다.

종합적인 architecture 모습은 아래와 같으며

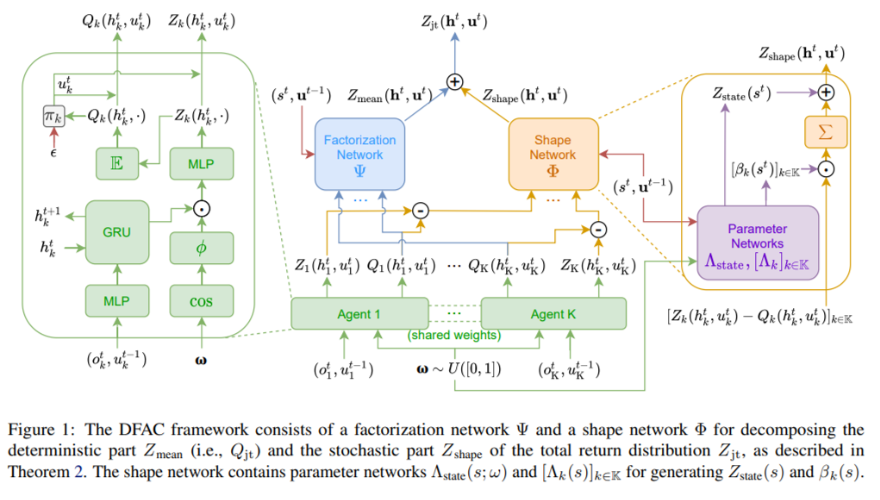
factorization network, agent 부분은 Z를 생성하는 것을 제외하면 QMIX와 비슷하고 shape network 는 윗 절의 후반부에서 설명한 내용들을 담고 있다. Z_state로 표현된 부분이 QMIX에서 second layer에 global_state를 통과한 FC layer를 첨가하는 부분을 모사한 것이라고 이해하면 편하다 .