Introduction
c51 방식이라고도 불림
RL agent의 reward를 Expectation 관점이 아닌 distribution의 관점에서 해석
Approximate 한 value distribution을 배우는 방향으로 Bellman equation을 apply 한다.
Distributional Bellman equation을 제시한다.
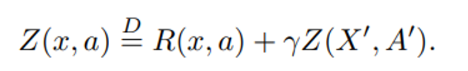
등호위에 D는 양쪽 항이 모두 같은 distribution을 갖고 있음을 의미한다.
Z는 value distribution이라고 부를 것이며 E[Z] = Q 를 만족한다.
여기서 진짜 등호가 아닌 위와 같은 등호를 쓰는 이유는 distribution에서 값을 뽑아 양변의 값이 같을 확률은 매우 낮기 때문이다.
- 논문에서 제시한 distributional RL의 장점?
1) multimodality로 인한 stable learning
2) nonstationary policy 에서의 학습으로 인한 effect를 피할 수 있음
Section3 Lemma 3
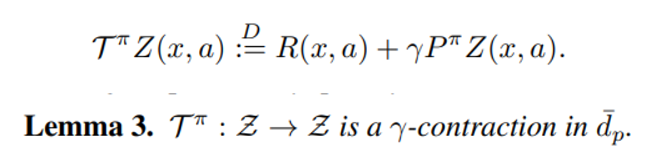
Wasserstein distance는 두개의 distribution 사이 거리를 측정하는 metric이며 distribution 에 대한 Bellman operator를 -contraction 해주기 때문에 이를 loss function으로 사용한다면 convergence를 보장받을 수 있다. (local or global optimum 인지는 확정할 수 없다)
section 4
distribution 이 가질 수 있는 가장 작은 값과 큰 값을 로 정의한다.
support 혹은 set of atom 이라고 불리는 z는 이 구간을 나누는 간격의 크기를 의미한다.
Learning 과정에서 z는 hyper-parameter로 정의되어 있고 우리가 학습하는 것은 각 z에 해당하는 확률값이다. (확률값이기 때문에 soft-max 처리)
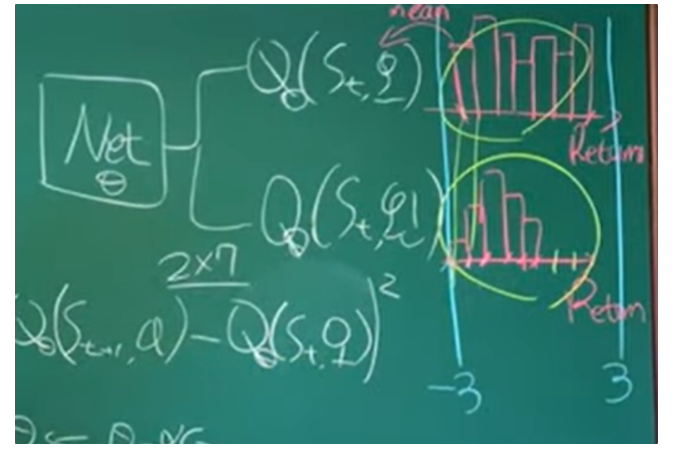
기존 DQN 과 distributional RL의 차이는 아래 그림을 참고하면 이해하기 편하다
section 4.2 - projection을 하는 이유
TD target 방식을 사용한 경우 Z의 목표값은 인데 distributional 형태로 이 꼴을 닮기 위해서는 위에 첨부된 칠판 사진에서 x축의 값이 의 꼴로 변해야 함을 의미한다.
하지만 이러한 연산을 진행할 경우 예시로 든 위의 경우 z축은 -3~3이었지만 support 의 간격도 변하고 값도 변하기 때문에 projection을 사용하는 것이다.
예를 들어 만약 의 값이 2.5이고 support 나눠지는 구간이 [2,3] 이라면 2.5에 해당되는 확률값은 내분의 역비율로 각각 원래 support 간격 기준인 2와 3에 대해 나눠지는 것이다.
구간은 분명히 겹칠 것이므로 하나의 point에 대해 두개의 확률 proportion이 더해지게 될 것이다.
Loss function
KL divergence == cross entropy를 최소화 하는 방향으로 한 distribution이 목표 distribution으로 향하게 만듦
알고리즘 해석

는 -greedy 한 방식으로 선정
next step t+1 에서 각 Q에 대한 distribution 의 mean을 비교해서 가장 Q값이 큰 action a*를 구할 수 있음
j는 support 의 index를 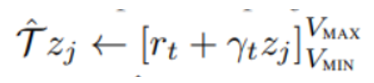
의미
각 support 에 대해 다음 distribution을 계산 (옆의 notation은 이 값이 max와 min 값으로 bound 하는 것을 의미)
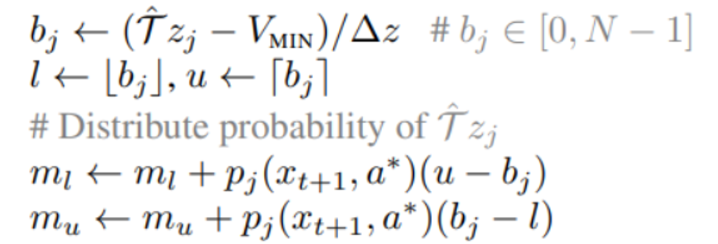
이 부분은 역내분점을 통해 각 support 값에 확률을 더해주는 과정 (section 4.2의 projection에서 설명함) 을 의미한다.
cross entropy 에서 mi는 target distribution, pi는 현재 내 distribution을 의미한다.
