B+ Tree

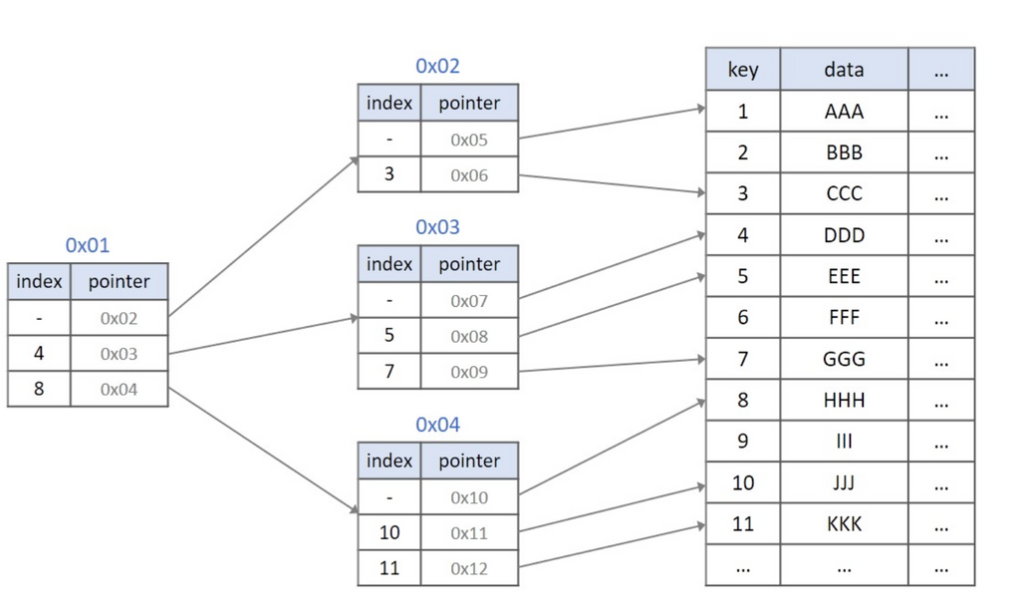
: 데이터의 빠른 접근을 위한 인덱스 역할만 하는 비단말 노드(not leaf)가 추가로 있음

(기존의 B- Tree와 데이터의 연결리스트로 구현된 색인 구조)

→ 선형 검색이 가능함

→ 실제 DB의 인덱싱은 B+ Tree로 이루어짐

DB 인덱싱

B+ Tree

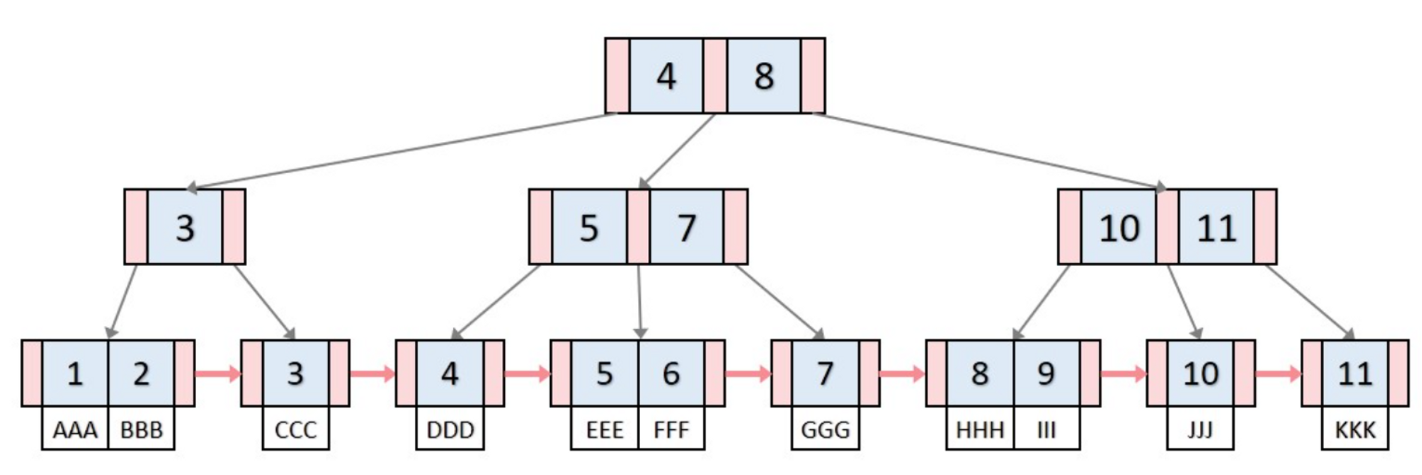
B- Tree에서 각 key 값이 data를 가지고 있다

B- Tree와 B+ Tree 차이점

• 모든 key, data가 리프노드에 모여있음.
  • B- Tree : 각 key마다 값 가짐/B+ Tree: 리프에 모든 data
• 모든 리프 노드가 연결리스트 형태
  • B- Tree는 형제 노드 검사 시, 다시 루트부터 검사 / B+ Tree는 리프노드에서 선형검사 가능
• 리프 노드의 부모 key는 첫 번째 key보다 작거나 같다

규칙

• 노드는 M개 ~ M/2개 자식
• M-1개 ~ [M/2]-1개 키
• 키가 N개, 자식 수는 N+1
• 최소 차수 : 자식 수의 하한값
  • 최소 차수가 t 라면, M = 2t - 1(t가 2라면 3차 트리, key의 하한은 1개)

삽입 과정

• 분할이 일어나지 않고(key의 수가 최대보다 적은 경우), 삽입 위치가 리프노드의 가장 앞 자리가 아닌 경우 → B- Tree와 똑같은 삽입 과정
  
• 분할이 일어나지 않고, 삽입 위치가 리프노드의 가장 앞 자리인 경우 → 삽입 후 부모 key를 삽입된 key로 갱신하고 data 삽입
  
• 분할이 일어나는 경우(key의 수가 최대인 경우)
  • 분할이 일어나는 노드가 리프노드가 아닌 경우
    • B- Tree와 똑같이 분할 진행
    • 중간 key를 부모 key로 올리고, 분할된 노드를 왼쪽 오른쪽 자식으로 설정
  • 분할이 일어나는 노드가 리프노드인 경우
    • 중간 key를 부모 key로 올리지만 오른쪽 노드에 중간 key를 포함하여 분할
    • 리프노드는 연결리스트이기 때문에 왼쪽 자식과 오른쪽 자식을 연결하여 연결리스트 형태 유지

삭제 과정

• 삭제할 key가 leaf node의 가장 앞에 있지 않은 경우 → B- Tree와 동일(그냥 삭제)
  
• 삭제할 key k가 리프노드의 가장 처음 key인 경우 : 이 경우 항상 leaf가 아닌 노드에 k가 index 내에 존재
  • 리프노드의 k 삭제
    • key의 개수가 최소 key의 개수라면, B트리의 삭제 과정 중 형제 노드의 key를 빌려오는 경우나 부모key와 병합하는 등 과정들은 동일
    • 리프노드가 병합할 때는 부모key와 오른쪽 자식의 처음 key가 동일하기 때문에 부모key를 가져오는 과정만 생략하고 왼쪽 자식과 오른쪽 자식을 병합만 함
    • 리프노드의 k를 삭제한 후, index내의 k를 index succesor로 변경

장단점

• 장점
  1. 블럭 사이즈를 더 많이 이용할 수 있음(key 값에 대한 하드디스크 엑세스 주소가 없기 때문)
  2. leaf 노드끼리 연결 리스트로 되어 있어서 범위 탐색에 매우 유리
• 단점
  1. B- Tree의 경우 최상 케이스에서 루트에서 끝날 수 있지만, B+ Tree는 리프까지 내려가야 함