자료구조

: 연속적인 메모리 위치에 저장되지 않는 선형 데이터 구조 (포인터를 사용해서 연결)각 노드는 데이터 필드와 다음 노드에 대한 참조를 포함하는 노드로 구성배열은 비슷한 유형의 선형 데이터를 저장하는 데 사용할 수 있지만 제한 사항이 있음배열의 크기가 고정되어 있어 미리

: index로 빠르게 값을 찾는 것이 가능함선언할 때 크기와 데이터 타입을 지정해야 함데이터가 계속 늘어날 때, 최대 사이즈를 알 수 없을 때는 부적합데이터 삽입, 삭제 비효율삽입 시 원래 값을 뒤로 밀어내고 해당 index에 덮어써야 함. 사이즈를 정해놓았기 때문에

: 입력과 출력이 한 방향으로 제한 ( LIFO : 후입선출)push : 데이터 삽입pop : 데이터 최상위 값 뺌isEmpty : 비어있는 지 확인isFull : 꽉 차있는 지 확인: 입력과 출력을 한 쪽 끝으로 제한 (FiFO : 선입선출)들어올 때는 rear로,

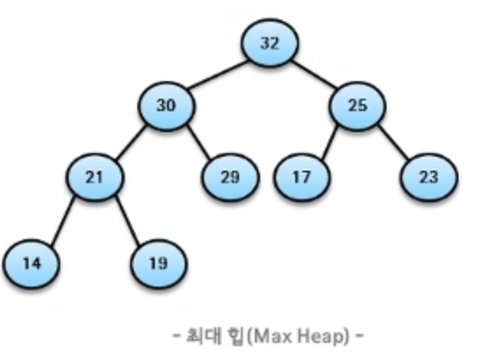
: 우선순위의 개념을 큐에 도입→ 우선순위가 높은 데이터가 먼저 나감시뮬레이션, 스케줄링, 수치해석배열, 연결리스트, 힙으로 구현(힙이 가장 효율적) → 힙 : 삽입(O(logN)), 삭제(O(logN)) : 우선순위 큐를 위해 만들어진 자료구조완전 이진 트리의 일

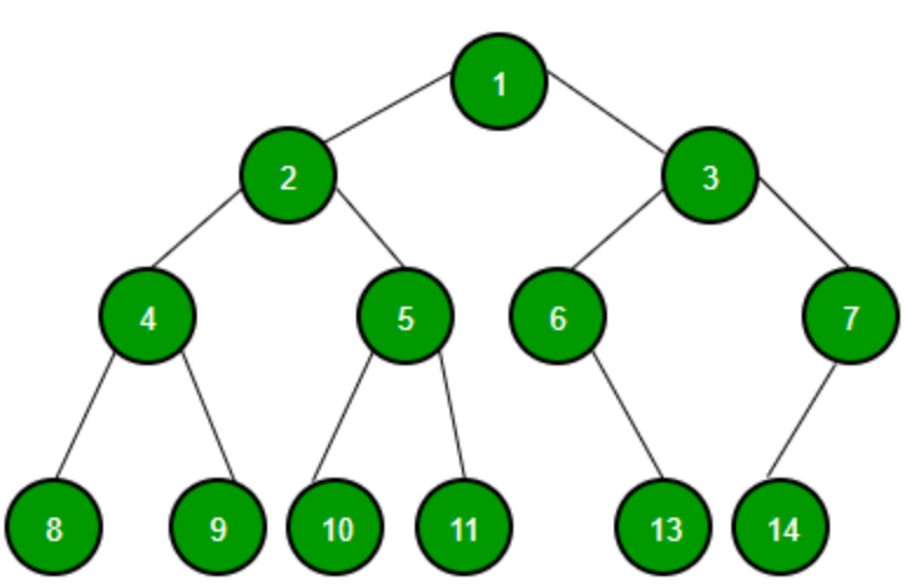
: node 와 edge 로 이루어진 자료구조사이클 X (사이클이 있다면, 트리가 아니고 그래프임)모든 노드는 자료형으로 표현 가능루트에서 한 노드로 가능 경로는 하나뿐노드의 개수가 N, edge 개수는 N-1각 루트를 순차적으로 먼저 방문(Root → 왼쪽 자식 →

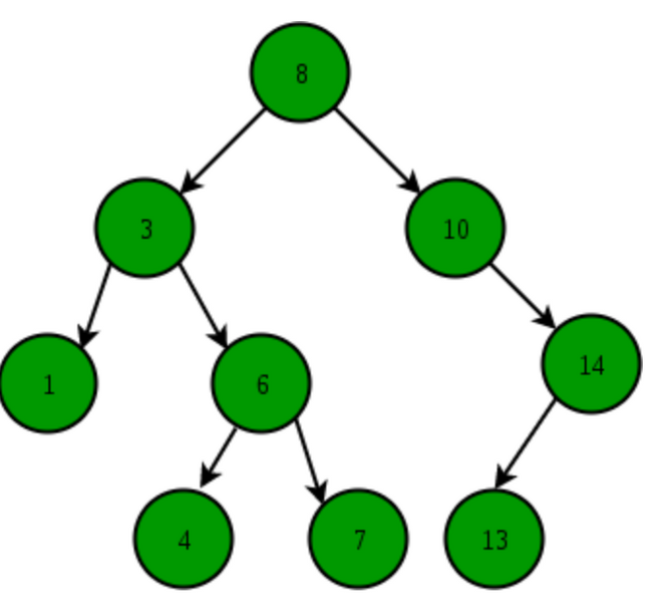
이진 탐색 + 연결 리스트이진 탐색 : 탐색에 소요되는 시간 복잡도 O(logN), but 삽입 삭제 불가능연결 리스트 : 삽입, 삭제의 시간 복잡도 O(1), but 탐색하는 시간 복잡도 O(N)이 두 개를 합쳐 장점을 모두 얻는 것이 이진 탐색 트리→ 효율적인 탐색

: 데이터를 효율적으로 관리하기 위해, 임의의 길이 데이터를 고정된 길이의 데이터로 매핑하는 것→ 해시 함수를 구현하여 데이터 값을 해시 값으로 매핑한다데이터가 많아지면, 다른 데이터가 같은 해시 값으로 충돌나는 현상 ⇒ Collision 현상적은 자원으로 많은 데이터

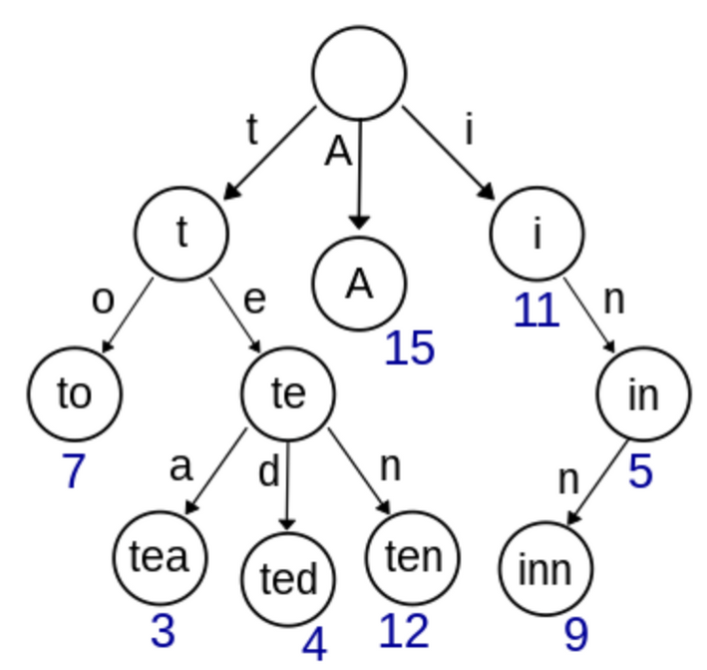
: 문자열에서 검색을 빠르게 도와주는 자료구조DFS 형태로 검색 시 : to, tea, ted, ten, A, i , in, inn문자열 탐색 시 시간복잡도 줄이기 위해→ 빠르게 탐색이 가능하지만 각 노드에서 자식들에 대한 포인터들을 배열로 모두 저장하고 있어 메모리를

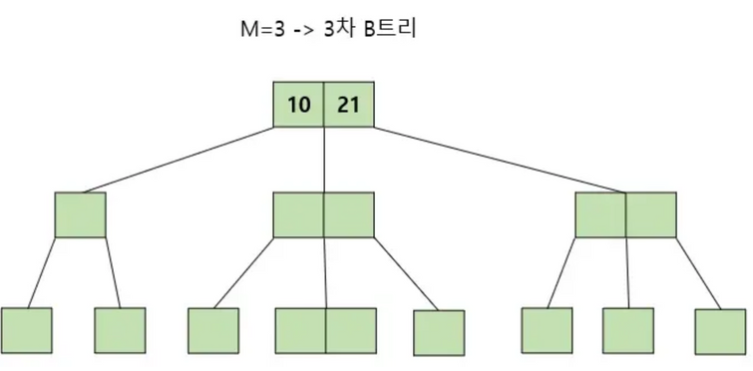
이진 트리하나의 부모가 하나의 자식균형이 맞지 않으면 검색 효율 급락⇒ 이진 트리 구조의 간결함, 균형만 맞다면 검색, 삽입, 삭제 모두 O(logN)의 성능을 기대할 수 있기에 개선하려고 함: 데이터베이스, 파일 시스템에서 널리 사용되는 트리 자료구조의 일종 이진

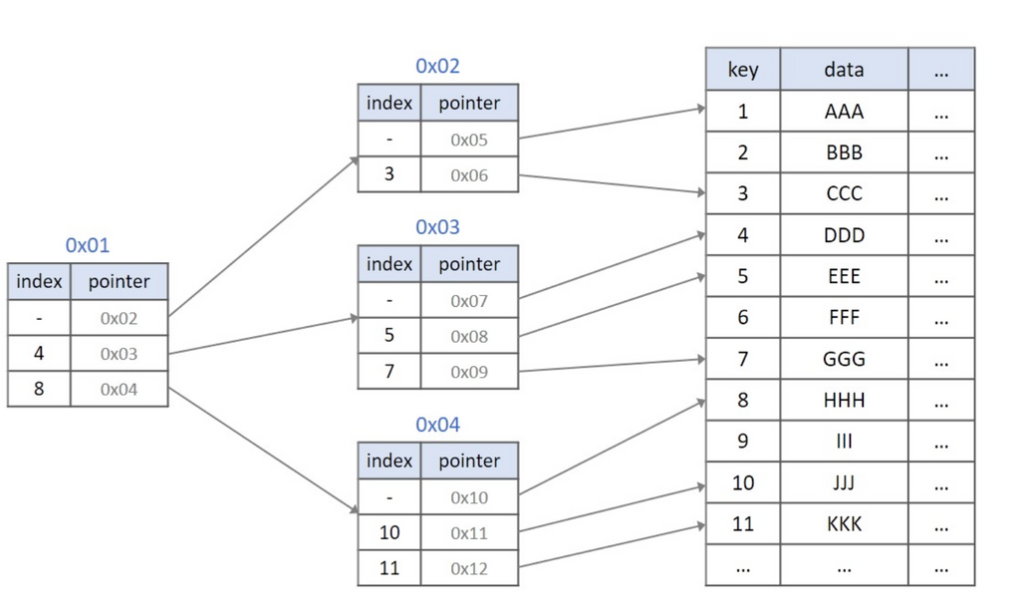
: 데이터의 빠른 접근을 위한 인덱스 역할만 하는 비단말 노드(not leaf)가 추가로 있음(기존의 B- Tree와 데이터의 연결리스트로 구현된 색인 구조)→ 선형 검색이 가능함→ 실제 DB의 인덱싱은 B+ Tree로 이루어짐DB 인덱싱B+ TreeB- Tree에서