[CS/PL] Programming Language : 3. Describing Syntax and Semantics

doooly·2024년 7월 27일

CS

목록 보기

2/3

✨ 본 포스트는 CONCEPTS OF PROGRAMMING LANGUAGES 교재를 기반으로 작성되었습니다

1. Definition of Language

Syntax : expression, statements, program units 의 형태 혹은 구조
Semantics: expression, statements, program units 의 의미

언어를 정의하는 것 ➡️ 문법과 그에 상응하는 해석 및 의미를 정의하는 것

Language에 사용되는 전문 용어들은 다음과 같다

sentence : 알파벳 문자열

language : sentence의 집합

lexeme : 의미를 가지는 가장 최소 단위의 문법 요소

token : 같은 의미를 가지는 lexeme의 범주

2. Formal Definition of Language in PL

PL에서 언어를 공식적으로 정의하는 방법은 다음과 같이 2가지 방법이 있다

1. Recognizers

recognizer은 입력된 문자열을 읽고 해당 문자열이 언어에 속하는지 여부를 결정함
recognizer에 의해 문장이 해석되지 않는다면, 해당 문장의 Syntax에 오류가 있음을 뜻함
ex) syntax analysis part of a compiler

2. Generators

generator은 특정 언어로 구사된 문장을 생성함
문장의 Syntax와 generator의 구조를 비교해 구문적 오류를 비교함
즉, generator으로 특정 문장을 생성할 수 없다면, 해당 문장의 Syntax에 오류가 있음을 뜻함

3. Context Free Grammer and BNF

3-1. CFG

자연어의 Syntax를 설명하는 언어 생성기
Noam Chomsky에 의해 발달됨
해당 문법으로 인해 만들어지는 문자열들을 정의함
👉 Production Rule을 나열
Nonterminal을 Terminal으로 만들어가는 과정을 나타냄
- Terminal : lexeme 혹은 token을 뜻함
- RULE이 하나 이상 존재한다면, 그 집합을 문법이라고 부름
기호
- Nonterminal Symbol : 대문자
- Terminal Symbol : 소문자
- 시작 Symbol : S

3-2. BNF

John Backus에 의해 발명됨
CFG를 프로그래밍 언어에 접목시킴
Derivation Rule을 나열
기호
- Nonterminal Symbol : <>
- Terminal Symbol : 소문자
fundamentals
- LHS(left hand side) : Nonterminal
- RHS(right hand side) : Nonterminal or Terminal

Derivatioin?

⇒ / ⇒*

BNF는 위와 같은 기호를 사용해, sentential form ⇒ sentence 형태로 Rule을 표현함

sentential form : 문장을 만들기 위해 등장하는 다른 요소들

sentence : terminal으로만 이뤄진 sentential form

leftmost derivation : 가장 왼쪽 terminal부터 변환

rightmost derivation : 가장 오른쪽 terminal부터 변환
👉 문법이 정확하게 정의된 언어라면, 이러한 변환 순서와 상관없이 일관된 결과를 도출하고 같은 의미를 가져야 함

Derivation Example

아래와 같은 BNF가 존재한다고 가정

<program> → <stmts>
<stmts> → <stmt> | <stmt> ; <stmts>
<stmt> → <var> = <expr>
<var> → a | b | c | d
<expr> → <term> + <term> | <term> - <term>
<term> → <var> | const

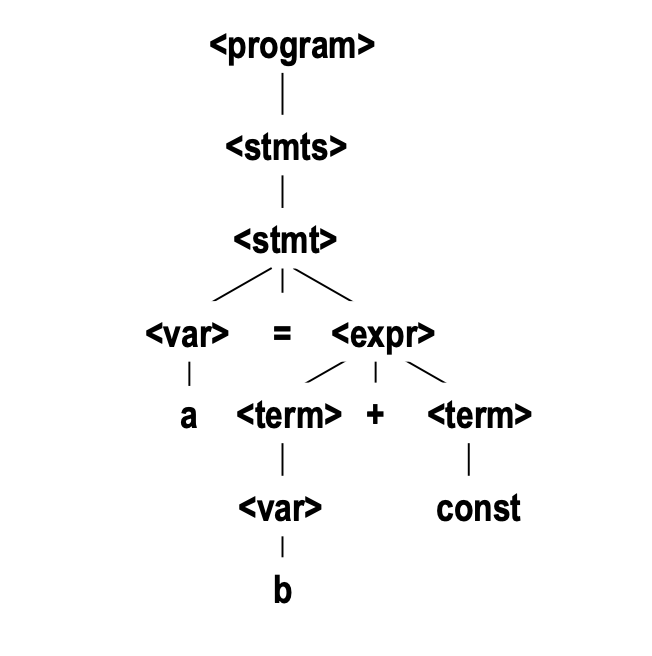
아래는 위의 BNF에 의해 만들어지는 특정 문자열, a = b + const 을 derivation하는 과정이다

<program> => <stmts> => <stmt>
					 => <var> = <expr>
					 => a = <expr>
					 => a = <term> + <term>
					 => a = <var> + <term>
					 => a = b + <term>
					 => a = b + const

3-3. Parse Tree

Derivation 과정을 계층적인 트리로 나타냄

parse tree == derivation tree == syntax tree
위의 Derivation Example의 유도 과정을 Parse Tree로 나타내면 다음과 같음

3-4. Ambiguity in Grammars

BNF를 통해 생성되는 문장은 그 유도 과정을 Parse Tree로 그려낼 수 있다
하지만, 명확하지 않은 문법을 사용한다면, 유도 과정에서 서로 다른 Tree를 그릴 수도 있다

아래와 같은 BNF를 사용하면 동일한 Syntax을 사용함에도 구조가 다른 Tree가 2개 이상 생성될 수 있다

<expr> → <expr> <op> <expr> | const
<op> → / | -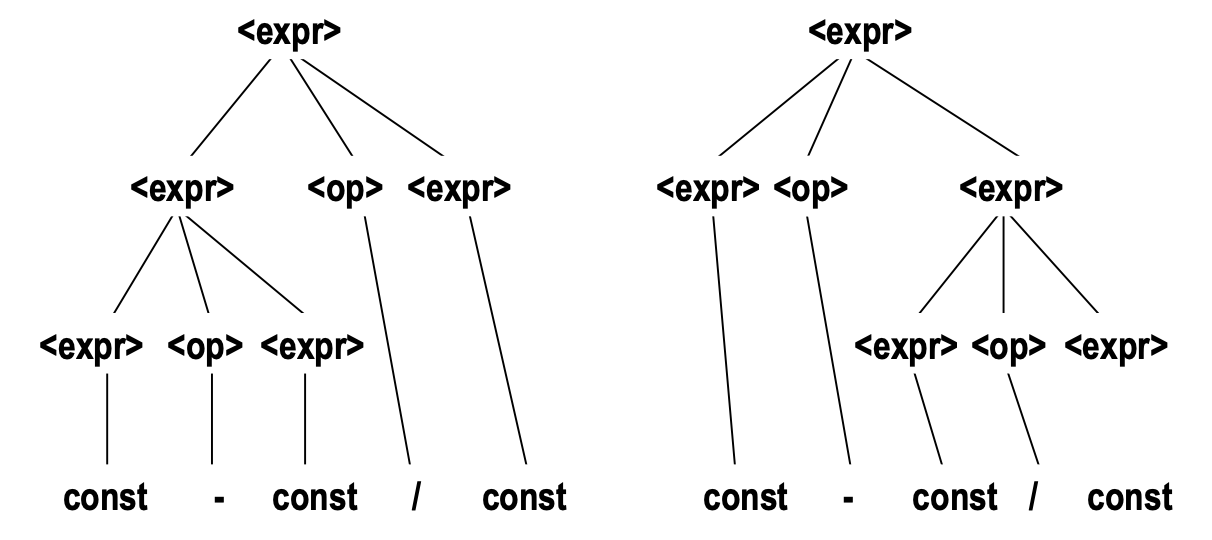

sentential form을 통해 derivation한 결과가 2개 이상의 서로 다른 Parse Tree를 생성한다면, 해당 문법은 ✨Ambiguous✨ 함을 뜻한다
이러한 모호한 문법을 사용하면, 각기 다른 Parse Tree에서 연산자의 depth가 다를 것이고, 이를 통해 도출된 문장의 의미 및 해석이 달라질 수도 있다

이러한 Ambiguous Grammar 문제는 ⭐️연산자의 우선 순위를 명확하게 정의함⭐️으로써 해결할 수 있다

ambiguous grammar ex :
<expr> -> <expr> + <expr> | const
unambiguous grammar ex :
<expr> -> <expr> + const | const

ambiguous grammer의 경우, 연산자를 기준으로 왼쪽과 오른쪽에 동일한 non-terminal 요소가 사용되었다
어느 non-terminal을 먼저 수행할지 우선 순위가 정해져있지 않기 때문에, 이러한 Ambiguous Grammer 문제가 발생한 것이다

unambiguous grammer example과 같이 연산자의 우선 순위, 즉 Associativity of Operators를 수정해 이러한 문제를 해결할 수 있으며, 이렇게 수정된 Unambiguous grammar는 sentence를 만드는 과정에서 항상 1개의 Parse Tree만을 생성함을 보장한다

3-5. EBNF

Extended BNF
기존의 BNF를 조금 더 사용하기 쉽게 확장한 버전이다
의미는 동일하나, 표기하기에 조금 더 편리하다는 장점이 있다

[ ]
- boolean : 해당 값이 나오거나 안나오거나, 즉 optional을 뜻함
- <proc_call> → ident[(<expr_list>)]
  - 함수 호출을 할 때 파라미터가 있을 수도 있고 없을 수도 있음
  - BNF : <proc_call> → ident | ident(<expr_list>)
{ }
- iteration : 0 ~ 무한대
- <ident> → letter { letter | digit }
  - BNF : <ident> → letter | letter<abc> <abc> → letter | digit | letter<abc> | digit<abc>
( )
- 여러 개 중 하나 선택
- <term> → <term> (+|-) const
  - +,-는 우선순위를 갖지 않음 / left associativity
  - +와 - 중 하나 택해서 연산

4. Static Semantics

semantics은 크게 두 분류로 구분된다
1.Dynamic Semantics

해당 문장이 하드웨어에서 어떻게 동작할 것인지, 의미를 나타냄
보통 semantics라고 불림

2.Static Semantics

의미와 큰 관련이 없음
Syntax, 즉 CFG만으로는 표현할 수 없는 것들을 나타내기 위해 사용됨
type checking, 블럭의 범위 분석, 변수 선언 위치, ...

4-1. Attribute Grammars

Parse Tree의 node에 추가적인 의미를 더하기 위해 적용됨
static semantic specification + compiler design 요소 포함
아래 3가지 definition이 추가된 CFG로 여겨짐
- 각 문법 기호 x에는 속성 값의 집합 A(x)가 존재함
  - labeling + 변수 뒤에 .을 사용해 속성을 나타냄
- 각 rule에는 non-terminal 요소의 속성을 정하는 attribute computation function이 존재함
- 각 rule은 속성의 일관성을 확인하는 predicate set이 존재함

4-1-1. Attributes

Rule이 $X_0$ → $X_1$ ... $X_n$ 의 꼴을 띤다고 가정했을 때, Attributes의 종류에 대해 알아보자
1. Synthesized attributes

$S(X_0) = f(A(X_1), ... , A(X_n))$
left node에서부터 위로 attribute가 영향을 끼침
sibling node의 attribute는 서로 영향을 끼치지 않음

2. Inherited attributes

$I(X_j) = f(A(X_0), ... , A(X_j)), for i <= j <= n$
root node의 attribute가 아래로 내려오며 left node의 attribute에 영향을 끼침
sibling node의 attribute도 영향을 끼칠 수 있음

3. Intrinsic attributes

tree 내부의 구조와 관계없이 외부 영향에 의해 left node들의 attribute가 결정됨

4-1-2. Grammars Example

Syntax
<assign> -> <var> = <expr>
<expr> -> <var> + <var> | <var>
<var> -> A | B | C

actual_type: synthesized for <var> and <expr>
expected_type: inherited for <expr>

위와 같은 Syntax를 정의할 때, 이에 대한 Attribute Grammar는 다음과 같이 작성할 수 있다

Syntax rule: <expr> → <var>[1] + <var>[2]

Semantic rules:
<expr>.actual_type <- <var>[1].actual_type

Predicate:
<var>[1].actual_type == <var>[2].actual_type
<expr>.expected_type == <expr>.actual_type

label을 달아 변수를 구분하고, .을 사용해 변수의 속성을 표시함
<var>[1]의 실제 타입에 따라 <expr>의 타입이 결정됨을 semantic rule을 이용해 명시함

Syntax rule: <var> → id

Semantic rule:
<var>.actual_type <- lookup (<var>.string)

<var>이 A, B, C를 뜻하고 있으므로, symbol table을 lookup한 결과가 <var>의 type으로 지정됨을 명시함

5. Dynamic Semantics

언어에서 내가 쓴 sentence가 어떤 meaning을 가질 것인지를 나타냄

5-1. Operational Semantics

하드웨어 기반 구현 및 시뮬레이션을 통해 언어의 의미, 결과를 보여줌
내가 만든 언어의 의미를 VM을 가지고 해석해주는 것
어떤 하드웨어든 abstraction시켜서 내 언어를 번역해주겠다 = VM
적당하게 Informal한 방법으로 나타낼 수 있음 (비정형화)
- 언어의 동작 방식을 코딩을 통해 보여줄 수 있음
language manual 등 informal하게 사용할 경우 좋지만, formal하게 사용해야 할 경우 동작 방식이 매우 복잡해짐

5-2. Denotational Semantics

수학적 함수로 내 언어의 상태를 표기하는 방식
가장 추상적인 semantics description method
recursive function theory / iteration을 재귀로 표현함
모든 언어 구성 요소에 대해서 함수 하나씩 맵핑해야 함
내 프로그램의 동작의 의미를 변수값을 바꿔주는 것으로 표현함
- 100% 표현 불가함
- 변수로 표현할 수 없는 동작이 존재함 → 100% 맵핑이 불가함
- 값이 바뀌는 것은 수학적 함수로 모두 표현 가능하나, 아닌 것도 존재함
동작 과정
- 각 언어 엔티티에 대한 수학적 객체 정의
- 언어 엔티티의 인스턴스를 해당 수학적 객체의 인스턴스에 매핑하는 함수를 정의
컴퓨터의 상태 s를 변수로 표현함
- $s = {<i_1, v_1>, <i_2, v_2>, …, <i_n, v_n>}$
VARMAP
- 현재 상태에서 $i_j$ 의 상태인 $v_j$ 를 출력하는 함수 정의
- $VARMAP(i_j, s) = v_j$
evaluation
- language 설계에 도움이 됨
- 프로그램의 정확성을 검증하는 데에 도움이 됨
- 너무 복잡하기 때문에 언어 사용자에게는 거의 쓸모가 없음

5-2-1. EX) Assign Statement

5-2-2. EX) Logical Pretest Statement

5-3. Axiomatic Semantics

논리로 파악 / 공리
entity 하나하나, 요소 하나하나를 axiom / inference rule로 정의함
프로그램 검증하는 용도로 사용함
- 모든 문장을 axiom으로 시작
- input : 시작 precondition
- 하나의 axiom을 거치면 post condition이되고, 이는 다음 문장의 precondition이 됨
- 마지막 문장의 postcondition과 예상 도출값을 비교해 프로그램의 정상 동작 유무 확인
- 역방향도 성립(입력조건이 같은지 다른지)
axiom
- 항상 참이 되는 주장을 만든다
- {P}S{Q} : 사전조건 + s + 사후조건
  - precondition
  - post condition(q로 표기됨)
  - “p 조건에서 s를 실행했을 때 q 상태가 된다”
    → 100프로 True 이면 Axiom / 아니라면 Assertion(주장)
- wP : weakest precondition
  - axiom을 만족시키며, 가장 약한 사전 조건
inference rule
- 항상 참이 되는 추론
- axiom 여러개를 연결해 만드는 추론
- 분수형태 : 위의 조건에 axiom이면, 아래 assertion도 axiom이 된다
evaluation
- 모든 언어에 대한 공리 및 추론을 만드는 것은 매우 어려운 일임
- 언어의 의미를 설명하고 언어를 증명하는 용도로 적합함
- 언어 사용자와 컴파일러 작성자에게는 거의 사용되지 않음

5-3-1. EX) Assignment

$(x = E): \{Q_{x->E}\} x = E \{Q\}$
위와 같은 Axiom이 있을 때, consequence rule은 아래와 같다

$\frac{\{P\}S\{Q\},P' => P, Q => Q'}{ \{P'\}S\{Q'\}}$

분자가 axiom인지 확인
분자가 axiom이라면, 분모가 axiom인지 확인
분모도 axiom이라면, 해당 Rule은 inference rule임

doooly

이전 포스트

[CS/PL] Programming Language : 2. Evolution of the Major Programming Languages

다음 포스트