1. 벡터의 내적
- 벡터의 내적은 같은 차원의 두 벡터가 주어졌을 때 벡터를 구성하는 각 성분을 곱한 후 이들을 더해 스칼라를 만들어 내는 연산이다.
u = (a, b)
v = (c, d)
u·v = a·c + b·d- 같은 벡터를 내적하면 벡터의 크기를 제곱한 결과가 나온다.
u = (a, b)
u·u = a·a + b·b = a^2 + b^2
∴ u·u = |u|^2 - 두 벡터의 사잇각을 θ라고 할 때 내적과 cos 함수의 관계는 다음과 같다.
u·v = |u|·|v|·cosθ벡터의 내적 활용
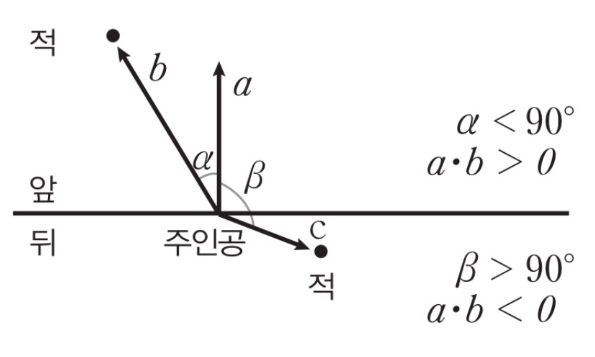
1) 앞뒤 판별
- 캐릭터의 시선을 u, 캐릭터에서 목표로 향하는 벡터를 v라고 할 때, 두 벡터의 내적 값에 따라 목표가 캐릭터의 앞에 있는지, 뒤에 있는지 파악할 수 있다.
- u·v > 0 (cosθ > 0 / 두 벡터 사이가 예각) : 목표가 캐릭터의 앞에 있다.
- u·v == 0 (cosθ == 0 / 두 벡터 사이가 직각) : 목표가 캐릭터의 옆에 있다.
- u·v < 0 (cosθ < 0 / 두 벡터 사이가 둔각) : 목표가 캐릭터의 뒤에 있다.
2) 시야 판별
- 시야각이 β이고, 캐릭터의 시선 단위벡터를 u, 캐릭터에서 목표물로 향하는 단위벡터를 v라고 할 때, 두 벡터의 내적 값에 따라 목표가 시야각 내에 있는지, 밖에 있는지 파악할 수 있다.
- u·v >= cos β/2 : 목표물이 시야 범위 안에 있다.
- u·v < cos β/2 : 목표물이 시야 범위 밖에 있다.
2. 벡터의 외적
- 벡터의 외적은 3차원 벡터에서만 사용 가능하다.
- 벡터의 외적은 두 벡터에 모두 수직인 벡터(== 법선 벡터)를 구하는 연산이다.
(서로 다른 요소만 조합하여 사용하는 특징이 있다.)
a = (x1, y1, z1)
b = (x2, y2, z2)
a x b = [(y1·z2 - y2·z1), (z1·x2 - z2·x1), (x1·y2 - x2·y1)]- 두 벡터의 사잇각을 θ라고 할 때 외적과 sin 함수의 관계는 다음과 같다.
(n은 두 벡터에 수직인 단위 벡터)
a x b = |a|·|b|·sinθ·n벡터의 외적 활용
1) 두 벡터의 평행 판별
- 외적을 했을 때 0이 나온다면 두 벡터는 평행한 벡터이다.
2) 좌우 판별
- 플레이어의 전방 벡터를 a, 플레이어에서 적을 향하는 벡터를 b, 게임 속 상향 벡터를 up이라고 할 때, up과 (a와 b의 외적)의 내적을 통해 적이 플레이어의 왼쪽에 있는지 오른쪽에 있는지 알 수 있다. (왼손 좌표계일 경우)
- up·(a x b) > 0 : 적이 플레이어의 오른쪽에 있음.
- up·(a x b) < 0 : 적이 플레이어의 왼쪽에 있음.
