1. 리스트(List)란?
: 순서를 가지는 데이터의 집합을 가리키는 추상자료형
- 동일한 데이터를 가지고 있어도 상관 X (중복 허용)
- 구현 방법에 따라 크게 두 가지로 나뉨
- 순차 리스트 : 배열을 기반으로 구현된 리스트
- 연결 리스트 : 메모리의 동적할당을 기반으로 구현된 리스트
2. 리스트 사용을 위한 주요 함수
addtoFirst(): 리스트의 맨 앞에 원소를 추가addtoLast(): 리스트의 맨 뒤에 원소를 추가add(): 리스트 특정 위치에 원소를 추가delete(): 리스트 특정 위치의 원소를 삭제get(): 리스트 특정 위치의 원소를 리턴
3. 순차 리스트
1) 구현 방법
- 1차원 배열에 항목들을 순서대로 저장
- 데이터의 종류와 구조에 따라 구조화된 자료구조를 만들어 배열로 구현할 수도 있음.
2) 데이터 접근
- 배열의 인덱스를 이용해 원하는 위치의 데이터에 접근 (ex. list[3])
3) 삽입 연산
- 삽입 위치 다음의 항목들을 뒤로 이동해야 함.
4) 삭제 연산
- 삭제 위치 다음의 항목들을 앞으로 이동해야 함.
5) 단순 배열을 이용한 순차 리스트 구현의 단점
- 자료의 삽입/삭제 연산 과정에서 연속적 메모리 배열을 위해 원소 이동이 필요
- 원소의 개수가 많고 삽입/삭제 연산이 빈번하게 일어날수록 작업 소요 시간이 크게 증가
- 배열의 크기를 미리 지정해야하기 때문에
- 실제 사용될 메모리보다 크게 할당하여 메모리 낭비 초래
- 할당된 메모리보다 많은 자료를 사용하여 새롭게 배열을 만들어 작업해야 하는 경우 발생
4. 연결 리스트
- 단순 배열을 이용한 순차 리스트의 단점을 보완한 자료구조
- 자료의 논리적 순서와 메모리 상의 물리적 순서가 일치하지 X, 개별적으로 위치하고 있는 원소 주소를 연결하여 하나의 전체적인 자료구조를 이룸.
- 링크를 통해 원소에 접근하므로 순차 리스트처럼 물리적인 순서를 맞추기 위한 작업 필요 X
- 자료구조의 크기를 동적으로 조정 가능 -> 메모리의 효율적 사용 가능
- 단, 구현이 배열을 이용한 순차 리스트보다 복잡하다.
1) 구성 요소
- 노드 (Node) : 연결 리스트에서 하나의 원소에 필요한 데이터를 갖고 있는 자료 단위
- 데이터 필드 : 원소의 값을 저장
- 링크 필드 : 다음 노드의 주소를 저장
- 헤드 (Head) : 리스트의 처음 노드를 가리키는 자료구조, 데이터 필드 없이 링크 필드만 존재
2) 단순 연결 리스트
- 노드가 하나의 링크 필드에 의해 다음 노드와 연결되는 구조
- 헤드가 가장 앞의 노드를 가리키고, 링크 필드가 연속적으로 다음 노드를 가리킨다.
- 최종적으로 Null을 가리키는 노드가 리스트의 가장 마지막 노드

2-1) 단순 연결 리스트 삽입 연산
- 'A', 'C', 'D'를 원소로 갖고 있는 리스트의 두 번째에 'B' 노드를 삽입할 때
1. 메모리를 할당하여 새로운 노드 new 생성

2. 새로운 노드 new의 데이터 필드에 'B' 저장

3. 삽입될 위치의 바로 앞에 위치한 노드의 링크 필드를 new에 복사

4. new의 주소를 앞 노드의 링크 필드에 저장

2-2) 단순 연결 리스트 삭제 연산
- 'A', 'B', 'C', 'D'를 원소로 갖고 있는 리스트의 'B' 노드를 삭제할 때
1. 삭제할 노드의 앞 노드 탐색

2. 삭제할 노드의 링크 필드를 선행 노드의 링크 필드에 복사
: B를 가리키는 노드가 아무 것도 없기 때문에 B가 삭제된 것과 같은 기능, 단 메모리 누수를 방지하기 위해 B가 점유하고 있는 메모리를 반환해야 한다.

3) 이중 연결 리스트
- 양쪽 방향으로 순회할 수 있도록 노드를 연결한 리스트
- 두 개의 링크 필드와 한 개의 데이터 필드로 구성 (링크 필드는 앞, 뒤 노드를 가리킴)

3-1) 이중 연결 리스트 삽입 연산
- cur가 가리키는 노드 다음으로 D 값을 가지는 노드를 삽입하는 과정
1. 메모리를 할당하여 새로운 노드 new를 생성하고 데이터 필드에 'D'를 저장

2. cur의 next를 new의 next에 저장하여 cur 다음 노드를 삽입할 노드의 다음 노드로 연결
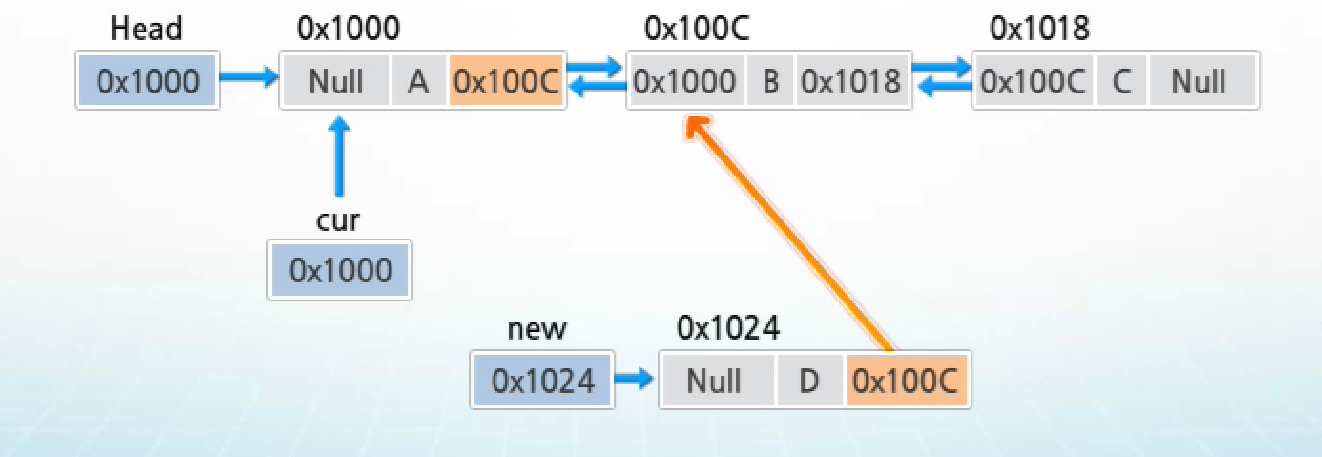
3. new의 값을 cur의 next에 저장하여 삽입할 노드를 cur의 다음 노드로 연결
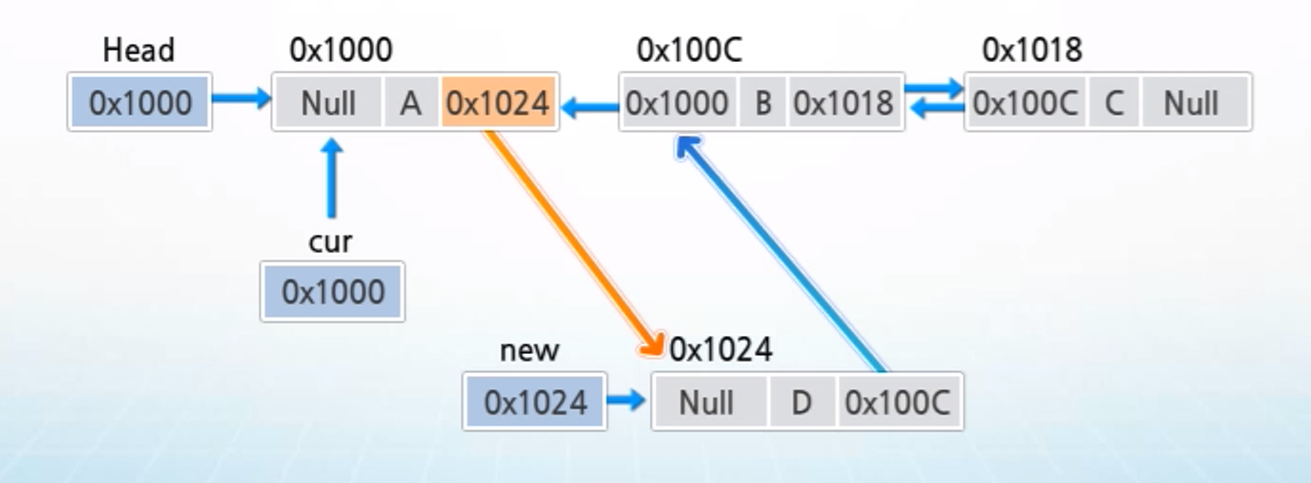
4. cur의 값을 new의 prev에 저장하여 cur을 new의 이전 노드로 연결
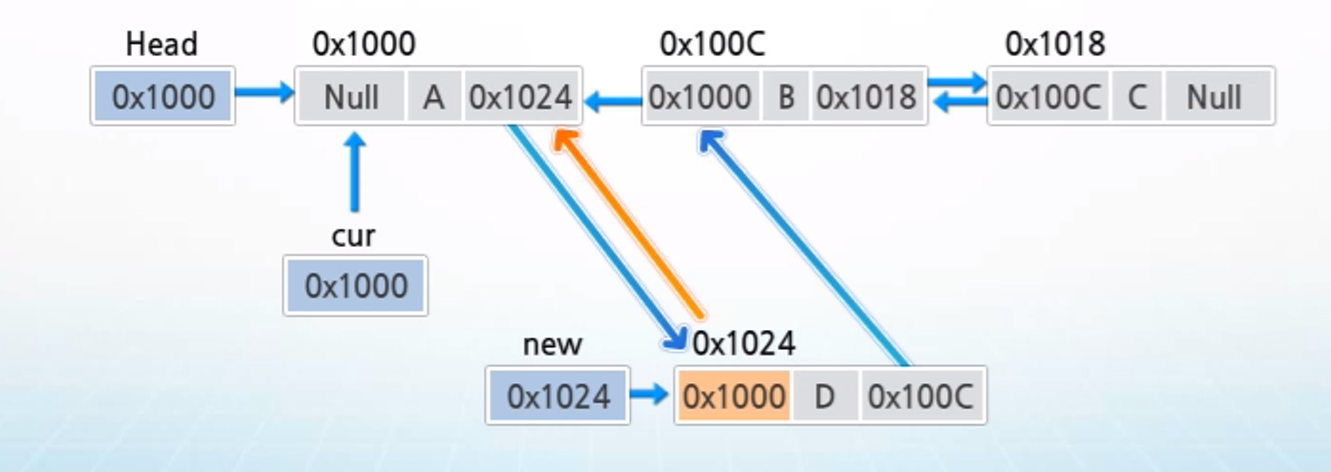
5. new의 next에 연결된 노드의 prev에 new의 값을 저장하여 삽입하려는 노드의 다음 노드와 삽입하려는 노드를 연결한다.
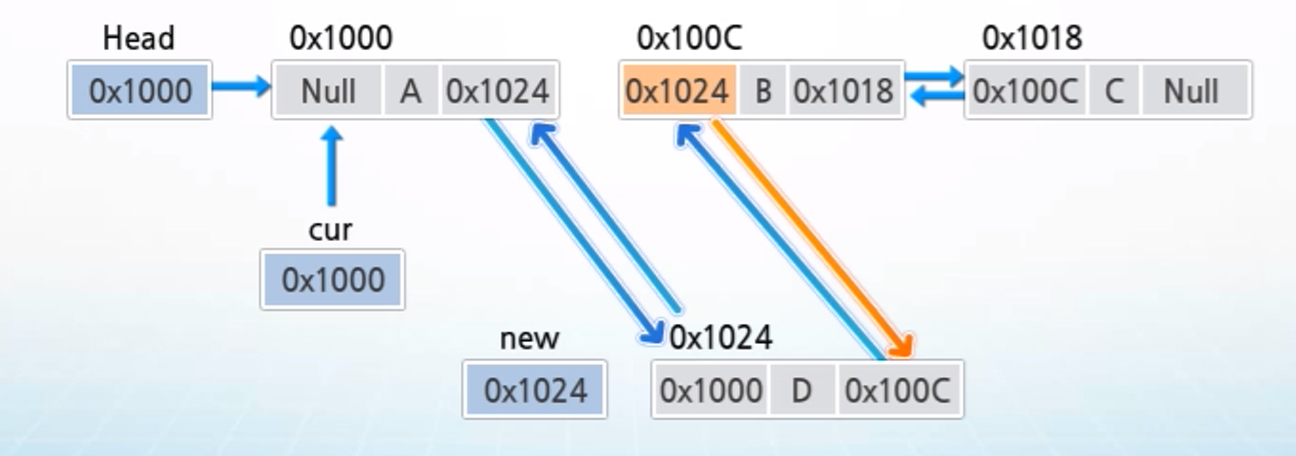
3-1) 이중 연결 리스트 삭제 연산
- cur가 가리키는 노드를 삭제하는 과정
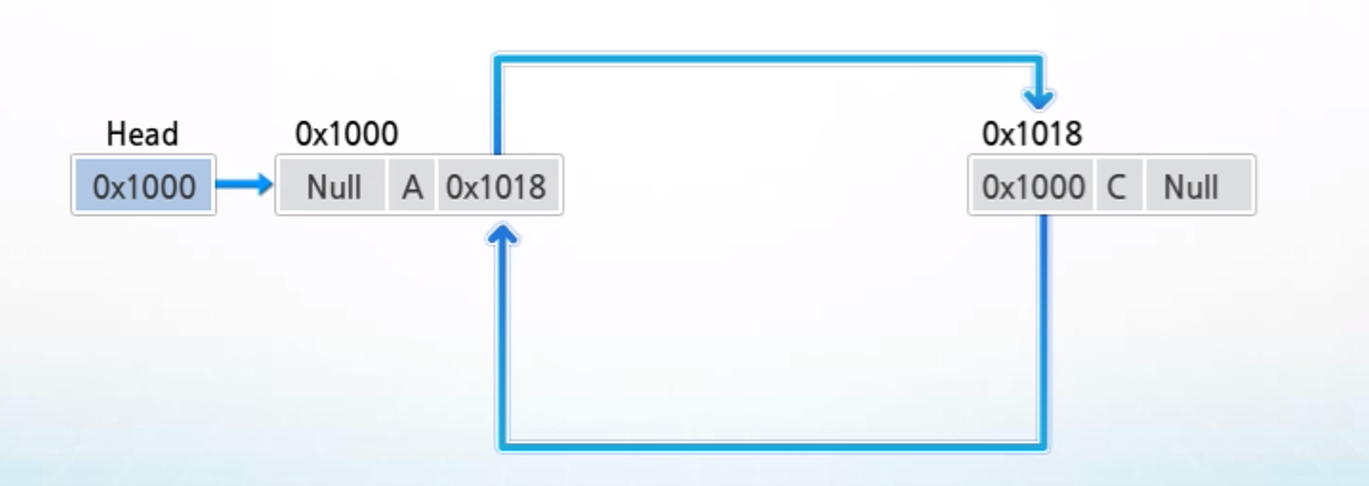
1. 삭제할 노드의 다음 노드의 주소를 삭제할 노드의 이전 노드의 next 필드에 저장하여 링크 연결
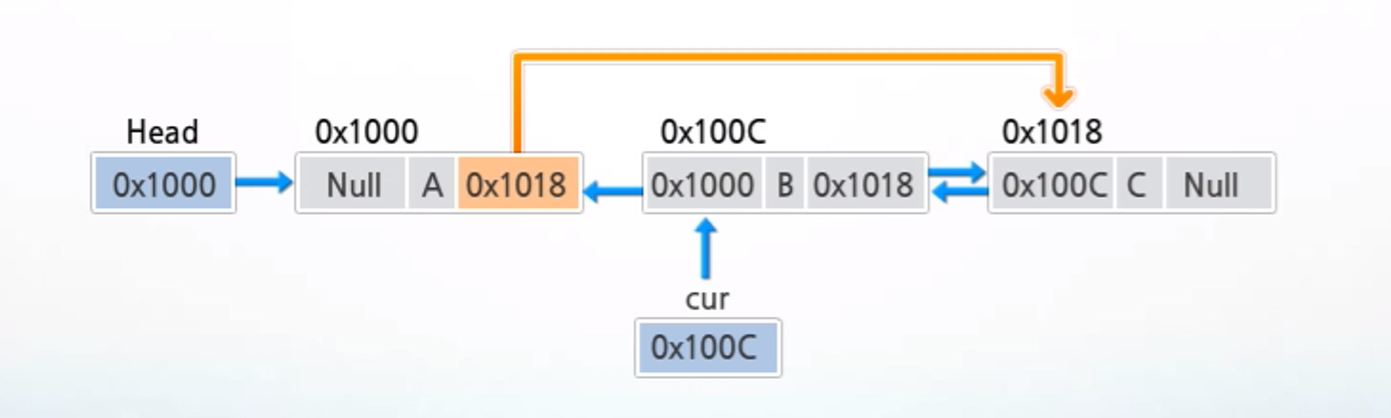
2. 삭제할 노드의 다음 노드의 prev 필드에 삭제할 노드의 이전 노드의 주소를 저장하여 링크 연결

3. cur가 가리키는 노드에 할당된 메모리를 반환
5. 삽입 정렬
1) 삽입 정렬의 과정
- 정렬할 부분 자료를 두 개의 부분집합 S와 U로 가정
- 부분집합 S : 정렬된 앞 부분의 원소들
- 부분집합 U : 아직 정렬되지 않은 나머지 원소들
- 정렬되지 않은 부분집합 U의 원소를 하나씩 꺼내서 이미 정렬되어있는 부분집합 S의 마지막 원소부터 비교하면서 위치를 찾아 삽입
- 삽입 정렬을 반복하면서 부분집합 S의 원소는 하나씩 늘리고 부분집합 U의 원소는 하나씩 감소
- 부분집합 U가 공집합이 되면 삽입정렬 완성
- 시간 복잡도 : O(n^2)
2) 예시 정렬
- {69, 10, 30, 2, 16, 8, 31, 22} 를 삽입 정렬하는 과정
1. 첫 번째 원소는 정렬된 부분집합 S로 생각하고, 나머지 원소들은 정렬되지 않은 부분집합 U로 생각

2. U의 첫 번째 원소 10을 S의 마지막 원소 69와 비교해 10 < 69 이므로 원소 10은 69의 앞 자리에 위치. 더 이상 비교할 원소 S가 없으므로 찾은 위치에 원소 10 삽입

3. U의 첫 번째 원소 30을 S의 마지막 원소 69와 비교해 30 < 69 이므로 69의 앞 자리 원소 10과 한 번 더 비교. 10 < 30 이므로 원소 10의 뒤에 삽입

4. U의 첫 번째 원소 2를 S의 마지막 원소 69와 비교해 2 < 69 이므로 69의 앞 자리 원소 30과 한 번 더 비교. 위 과정과 마찬가지로 비교 반복하여 최종적으로 가장 앞 자리에 삽입

5. U의 첫 번째 원소 16을 S의 마지막 원소 69와 비교해 16 < 69 이므로 69의 앞 자리 원소 30과 한 번 더 비교. 위 과정과 마찬가지로 비교 반복하여 최종적으로 10의 뒤에 삽입
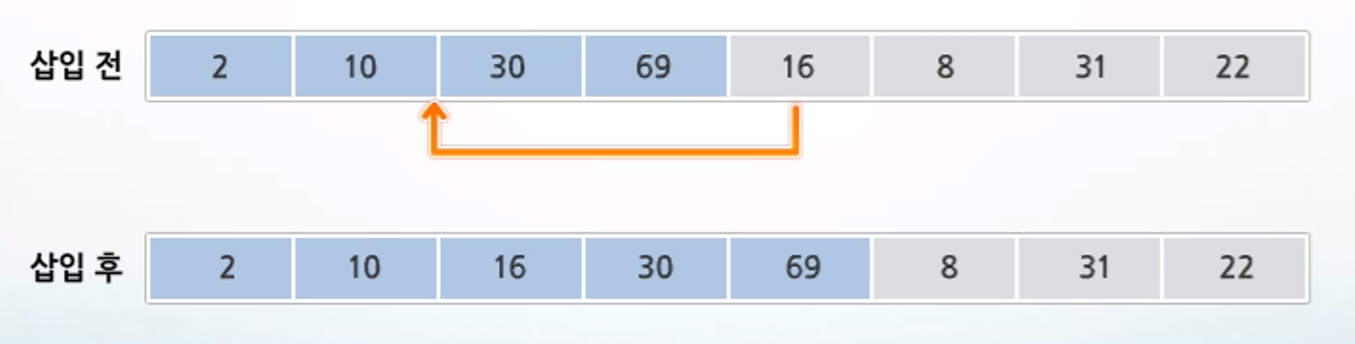
6. 나머지 원소 8, 31, 22도 위 과정과 같이 비교 반복하여 최종적으로 {2, 8, 10, 16, 22, 30, 31, 69} 순으로 정렬됨.

6. 병합 정렬
1) 병합 정렬의 특징
- 여러 개의 정렬된 자료의 집합을 병합하여 한 개의 정렬된 집합으로 만드는 방식
- 분할 정복 알고리즘을 활용하여 자료를 최소 단위의 문제까지 나눈 후에 차례대로 정렬하여 최종 결과를 얻어냄 (Top-Down 방식)
- 시간 복잡도 : O(nlogn)
2) 예시 정렬
- {69, 10, 30, 2, 16, 8, 31, 22} 를 삽입 정렬하는 과정
1. 분할 단계 : 전체 자료 집합에 대해 최소 크기의 부분집합이 될 때까지 분할 작업 반복

2. 병합 단계 : 2개의 부분집합을 정렬하면서 하나의 집합으로 병합
- 서브 리스트들을 두 개씩 묶고, 두 리스트의 첫 원소들을 비교해 작은 것부터 result에 추가한다. 추가한 원소는 해당 리스트에서 삭제한다.
- 한 서브 리스트에만 원소가 남게 되는 경우 해당 리스트 앞 원소부터 차례대로 result에 추가한다.
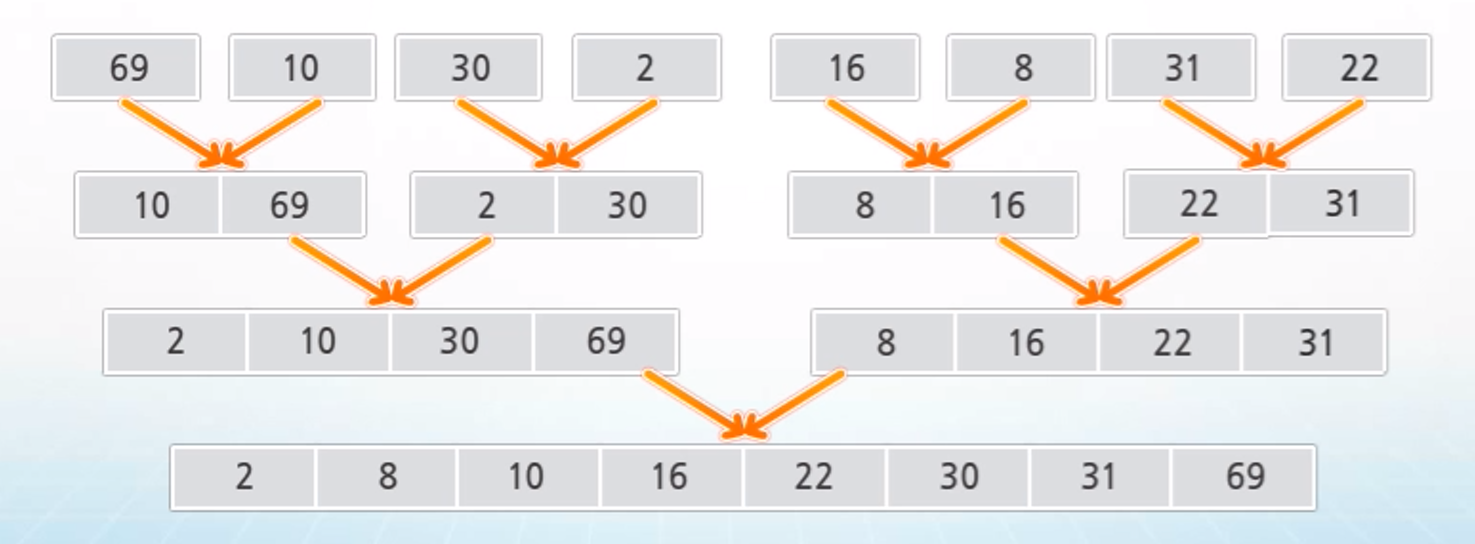
ex. [10 69][2 30] 서브 리스트 병합
- 각 리스트의 첫 번째 원소인 10과 2를 비교하면 2< 10이므로 result : 2 / 잔여 리스트 : [10 69][30]
- 10과 30을 비교하면 10 < 30이므로 result : 2 10 / 잔여 리스트 : [69][30]
- 69와 30을 비교하면 30 < 69이므로 result : 2 10 30 / 잔여 리스트 : [69]
- 한 쪽 리스트만 남았으므로 해당 리스트의 앞 원소부터 result에 추가 result : 2 10 30 69
