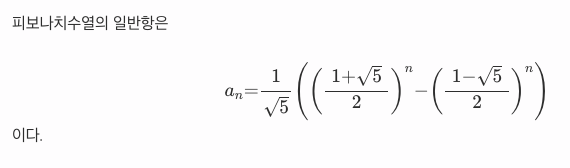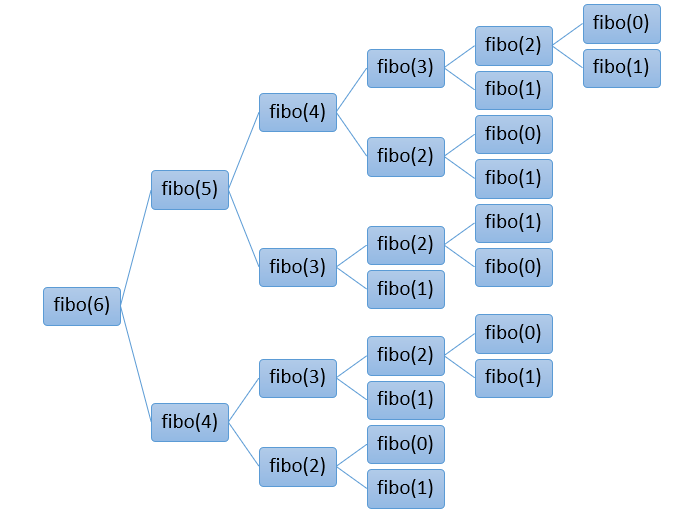
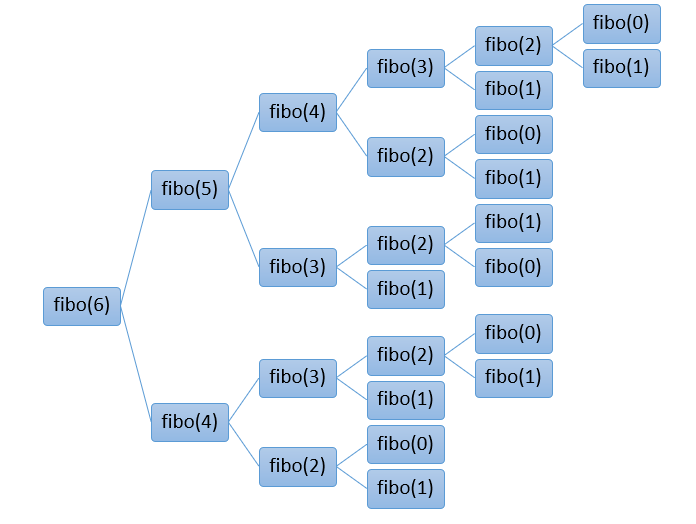
Try 1: 재귀함수 이용

const solution = (n) => {
  // if (n === 0) {
  //   return 0;
  // } else if (n === 1) {
  //   return 1;
  // }

  if (n <= 1) {
    return n;
  }

  // while (n > 0) {
    return solution(n - 1) + solution(n - 2);
  // }
};

처음 코드..

while문이 없어도 어차피 if문에서 리턴값으로 끝내는데.. 필요가 없었다
그리고 if문 수정함 (주석 처리한게 내가 바보같이 해둔거)
그리고 시간 복잡도는 O(2^n)으로 n 값에 41이상 들어가면 2^41 = 2,199,023,255,552 즉 필요한 연산이 약 2억번정도가 나오니까.. 2초 이상이 걸린다.
여기서 n이 1만 더 커져도 이전 피보나치 수를 구하는 데 필요한 시간 * 2배가 필요하다.
n = 50일 때부터는 이제 거의 1000,000초가 필요함..(거의 11일 가량 소요..)

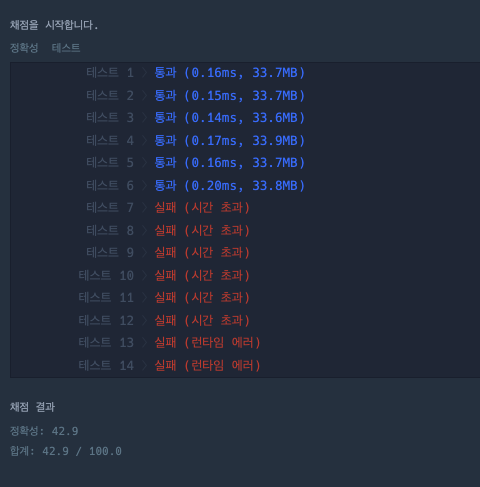
그래서인지... 망햇다.

반복문 -> 재귀 (꼬리재귀)
꼬리재귀 -> 반복문 (스택)
서로 변환 가능..!!

재귀 호출 대신 for문을 사용해서 첫 번째, 두 번째, 세 번째, ..., n번째 피보나치 수를 순서대로 구하자
이러한 풀이 방식을 동적 계획법(Dynamic Programming)이라고 함
n번째 피보나치 항을 여러 번 계산한다고 해서 그 값이 달라지지 않는다. 즉, 한번 구한 항을 기록(memoization) 해 둔 다음, 그 값이 필요할 때 꺼내쓸 수 있다면 굉장히 효율적일 것이다.

동적계획법의 알고리즘은 아래와 같다.
1. 문제를 부분 문제로 나눈다.
2. 가장 작은 문제를 해를 구한 뒤, 테이블에 저장한다.
3. 테이블에 저장되어있는 데이터로 전체의 문제의 해를 구한다.

점화식:피보나치, 병합정렬 이런 것 들..

subproblem이 지수적 감소: 이분탐색 (꼬리재귀라서 반복문으로 많이 씀)
subproblem이 나눠짐: 분할정복
subproblem이 여러번 필요: dynamic program (동적계획법) ~ 이름 멋잇어서 적은 알고리즘 (피보나치가 가장 대표적인 예 일반 재귀도 좋지만 동적계획법이 더 빠름)

https://blog.encrypted.gg/943
참고문헌
https://velog.io/@devjade/피보나치-수열-효율적으로-구현하기Dynamic-programming
https://alithedeveloper.tistory.com/m/24?category=996348

Try 2 동적 계획법

function fib(n) {
  const result = [0, 1];
  for (let i = 2; i <= n; i++) {
    const a = result[i - 1];
    const b = result[i - 2];
    result.push(a + b);
  }
  return result[n];
}

Try 3 피보나치 상수시간으로 구하는 법

상수시간 안에 피보나치 푸는 법도 있음.. https://suhak.tistory.com/81

이따가 할거임