자료구조 및 알고리즘

---

💎 트리

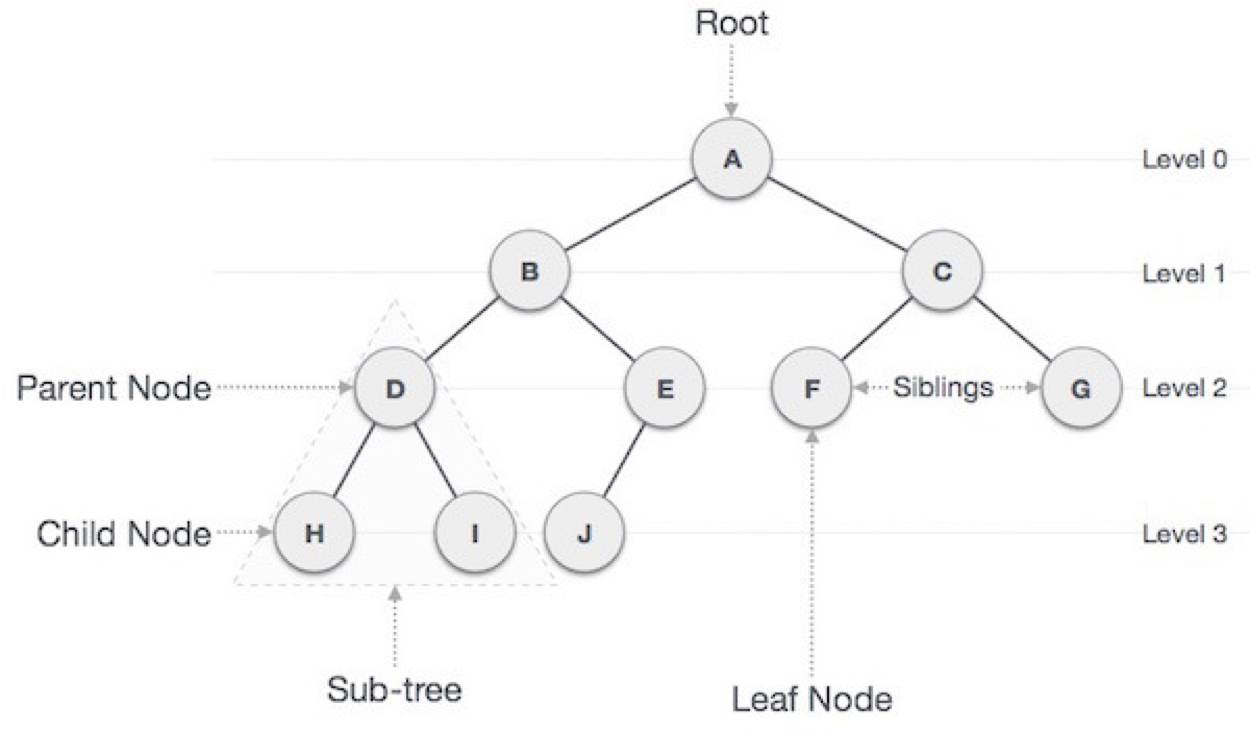
📘 정의

그래프의 일종으로 회로가 없고 서로 다른 두 노드를 연결하는 간선이 하나뿐인 그래프

📘 특징

1. 루트 정점을 제외한 모든 정점은 반드시 단 하나의 부모 정점을 가진다.

트리가 아닌 예

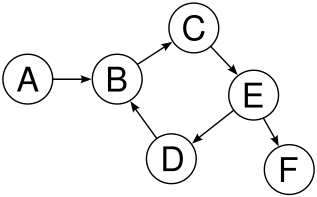
출처: 위키백과

• B 노드의 부모가 A, D로 두개 이상이므로 트리가 아니다.

2. 정점이 N개인 트리는 반드시 N-1개의 간선을 가진다.

• 정점노드 하나당 부모를 가리키는 간선은 단 하나만 갖는다. 반면 루트노드는 부모노드가 없으므로 간선의 개수는 정점의 개수보다 하나 작아야한다.

3. 루트에서 특정 정점으로 가는 경로는 유일하다.

• 만약 경로가 유일하지 않다면 루트와 특정 정점 사이에 분기점이 있어야한다.
  이 경우 부모노드가 2개 이상인 노드가 있어야하므로 트리라 할 수 없다.

트리가 아닌 예

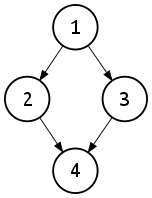
출처: 위키백과

• rootnode인 1에서 leafnode인 4로 가는 방법이 a) 1 -> 2 -> 4, b) 1 -> 3 -> 4 로 두가지인 것은 4의 부모노드가 2개이기 때문이다. 이 경우 트리라 할수 없다.

📘 구현

그래프에 일종이므로 인접 행렬이나 인접 리스트로 구현가능하다.

💎 이진 트리

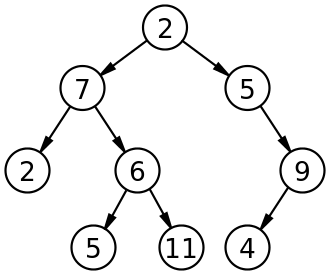
출처: 위키백과

정의

각각의 노드가 최대 두 개의 자식 노드를 가지는 트리 자료 구조로, 자식 노드를 각각 왼쪽 자식 노드와 오른쪽 자식 노드라 부른다.

📘 종류

1. 완전 이진 트리

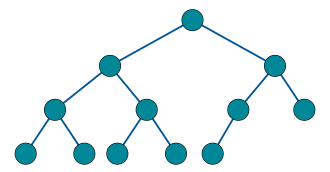
출처: 위키백과

• 마지막 level을 제외한 모든 level의 노드가 포화 상태여야하며, 마지막 level의 노드들은 최대한 왼쪽에 있는 이진 트리

2. 포화 이진 트리

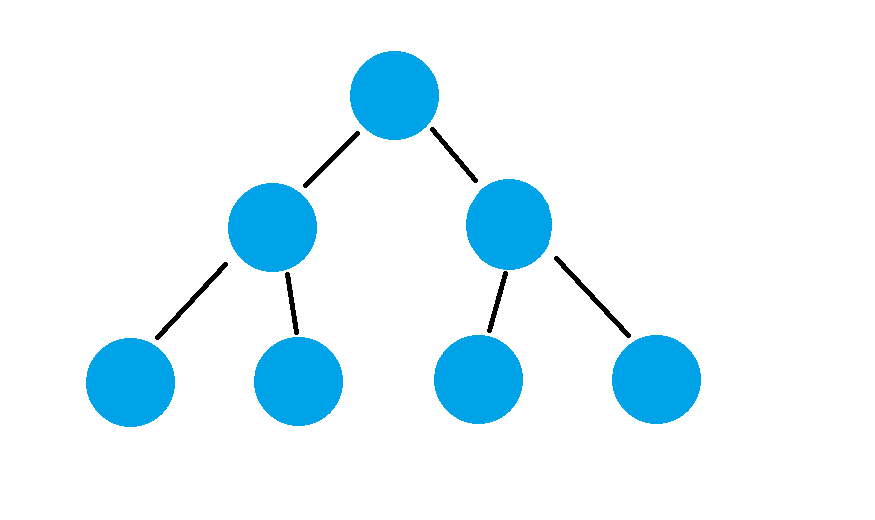
• 모든 leafnode가 동일한 level을 가지며, leafnode을 제외한 모든 노드가 2개의 자식 노드를 가지는 이진트리

3. 편향 이진 트리

• 모든 부모노드들이 하나의 자식노드를 가지며 한쪽으로 일정하게 치우친 이진트리

📘 특징

1. 정점이 N개인 이진트리는 최악의 경우 높이가 N이 될 수 있다.

2. leafNode가 $N$개인 포화 이진트리의 높이는 $log_2N$이다.

• 포화 이진 트리의 경우 높이가 $h$때 leafNode의 개수 N은 $2^{h}$ 이므로
  $h = log_2(N)$이다.

3. 정점이 $N$개인 완전 이진트리의 높이는 $[log_2N]$이다.

• 정점의 개수가 $N$개인 완전 이진 트리의 높이를 $h$라 하자.
  이 때 $2^{h} \le N < 2^{h+1}$이므로 로그의 성질에 의해 $h \le log_2N < h+1$이 되어
  높이 $h$는 $[log_2N]$이 된다.

📘 이진 트리 구현

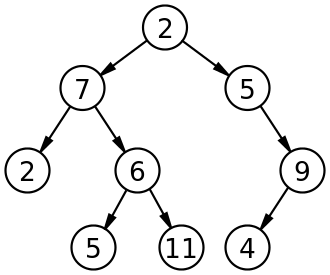
1. 배열을 이용

// 0번 인덱스는 제외한다.
// 왼쪽 자식 노드의 index는 부모노드 index의 2배
// 오른쪽 자식 노드의 index는 부모노드 index의 2배 + 1
const binaryTree = [
  null,
  // 1
  2,
  //2*1, 2*1+1
  7, 5
  //2*2, 2*2+1, 2*3, 2*3+1 
  2, 6, undefined, 9
  //2*4, 2*4+1, 2*5, 2*5+1, 2*6, 2*6+1, 2*7, 2*7+1
  undefined, undefined, 5, 11, undefined, undefined, 4, undefined
  
]

• 장점: 노드의 위치를 index에 의하여 쉽게 접근할 수 있다.
• 단점: 특정 트리에서 공간의 낭비가 심할 수 있다.

2. 연결 리스트를 이용

class Node{
  constructor(newValue) {
    this.data = newValue;
    this.left = null;
    this.right = null;
  }
}

class BinaryTree {
  constructor(node) {
    this.root = node;
  }
  
  display() {
  	const queue = new Queue();
    queue.enqueue(this.root);
    
    while(queue.size) {
      const currNode = queue.dequeue();
      console.log(currNode.data)
      if(currNode.left) queue.enqueue(currNode);
      if(currNode.left) queue.enqueue(currNode);
    }
  }
}

• 장점: 기억 장소를 절약할 수 있고, 노드의 삽입과 삭제가 용이하다.
• 단점: 이진 트리가 아닌 일반 트리의 경우에는 각 노드의 차수만큼 가변적인 포인터 필드를 가져야 하기 때문에 접근상의 어려움이 따른다.