
이 글은 이 영상을 바탕으로 작성되었습니다.
삭제
규칙
RB tree에서 삭제되는 노드의 자식의 수에 따라 삭제되는 색이 달라질 수 있다.
삭제되는 색
삭제하려는 노드의 자식이 없거나 하나라면 삭제되는 색 = 삭제되는 노드의 색
삭제하려는 노드의 자식이 둘이라면 삭제되는 색 = 삭제되는 노드의 successor의 색
이진트리의 successor는 간단히 말해 해당 노드의 오른쪽 자식의 서브트리 내 가장 작은 값.
규칙 위반 수정하기
삭제되는 색이 red라면 RB tree의 어떠한 속성도 위반하지 않는다.
하지만 black이라면 RB tree의 2, 3, 4, 5 속성을 위반할 수 있다.
레드블랙 트리의 속성에 대해선 여기에서 정리했다.
2번 속성 위반 수정하기
root 노드의 색을 red -> black으로 조정
이 경우를 제외하면 검은 색이 삭제되었을 때는 항상 5번 속성을 위반하게 된다.
5번 속성 위반 수정하기
5번 속성을 만족시키기 위해서 삭제된 색의 위치를 대체한 노드에 extra black을 부여한다.
extra black은 경로에서 black의 수를 카운트할 때 하나의 black으로 카운트된다.
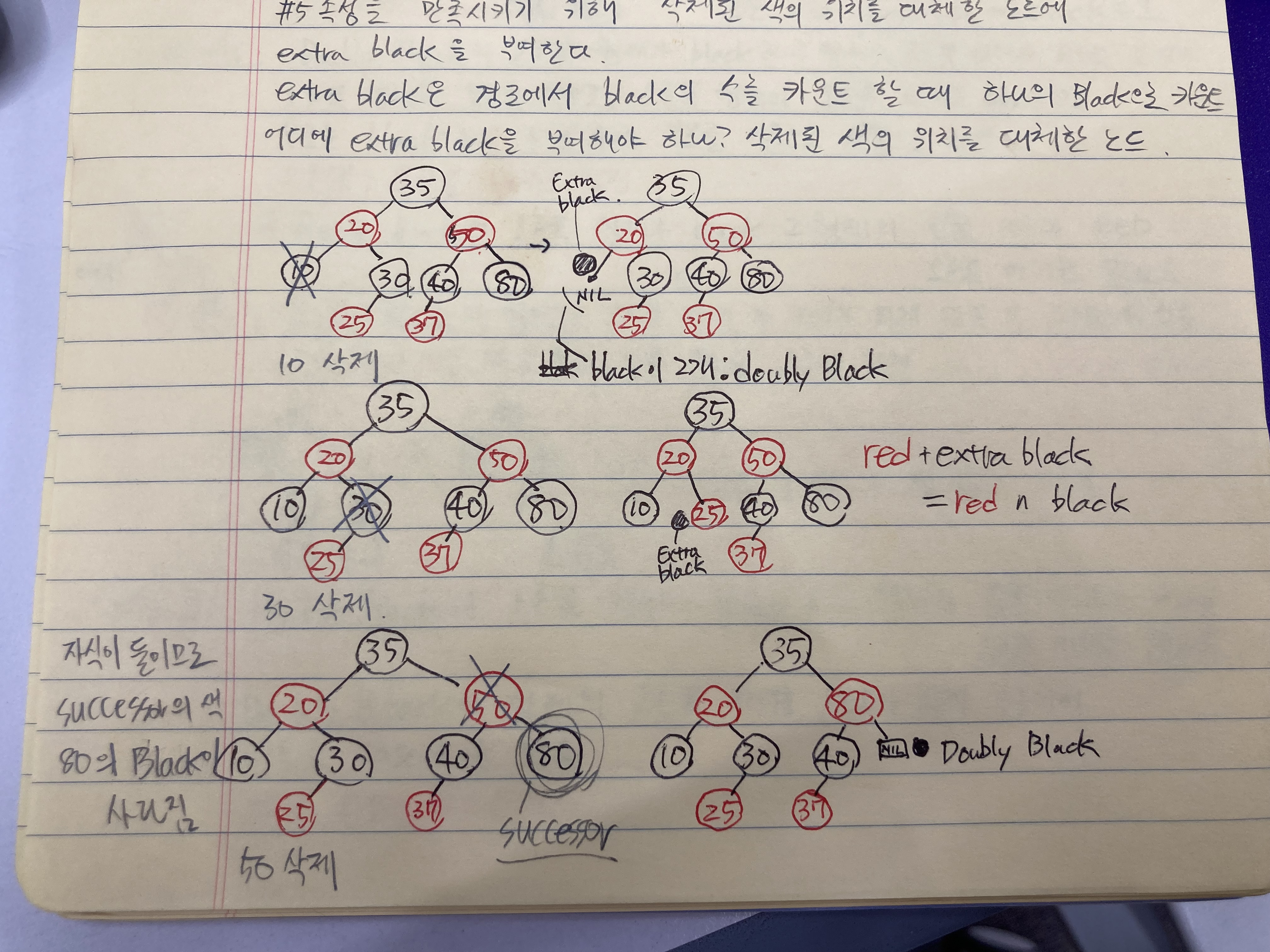
자녀가 없거나, 하나이거나, 둘인 경우 삭제되는 색과 extra black이 어디에 붙는지 한번 그려보았다.
extra black 해결하기
red 노드에 extra black이 붙는 경우를 red and black, black 노드에 extra black이 붙는 경우를 doubly black이라고 부른다.
red and black은 간단하다. 그냥 black으로 색을 바꾸면 RB tree의 속성을 위반하지 않고 해결할 수 있다.
문제는 doubly black이다. 이는 총 4가지 케이스로 분류된다.
doubly black 해결하기
4가지 케이스를 나누는 기준은 doubly black의 형제의 색과 그 형제의 자식들의 색이다.
그리고 이 4가지 케이스는 궁극적으로 해결 가능한 케이스인 case 4를 만드는 방향으로 진행된다.
- doubly black의 오른쪽 형제가 black & 그 형제의 오른쪽 자식이 red
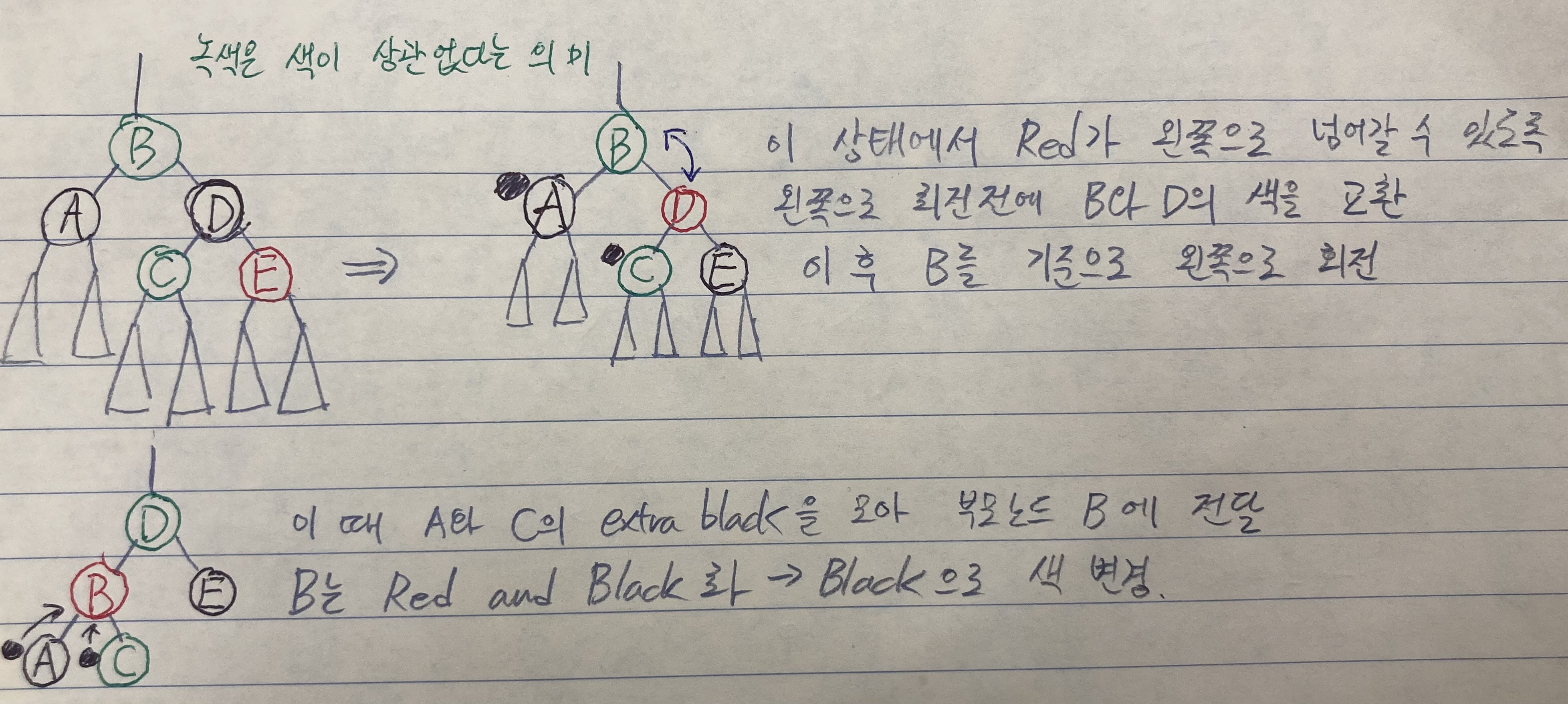
case 4.
doubly black의 오른쪽(왼쪽) 형제가 black & 그 형제의 오른쪽(왼쪽) 자식이 red일 때
오른쪽(왼쪽) 형제는 부모의 색으로, 오른쪽(왼쪽) 형제의 오른쪽(왼쪽) 자식은 black으로,
부모는 black으로 바꾼 후에 부모를 기준으로 왼쪽(오른쪽)으로 회전
- doubly black의 오른쪽 형제가 black & 그 형제의 왼쪽 자녀가 red, 오른쪽 자녀는 black
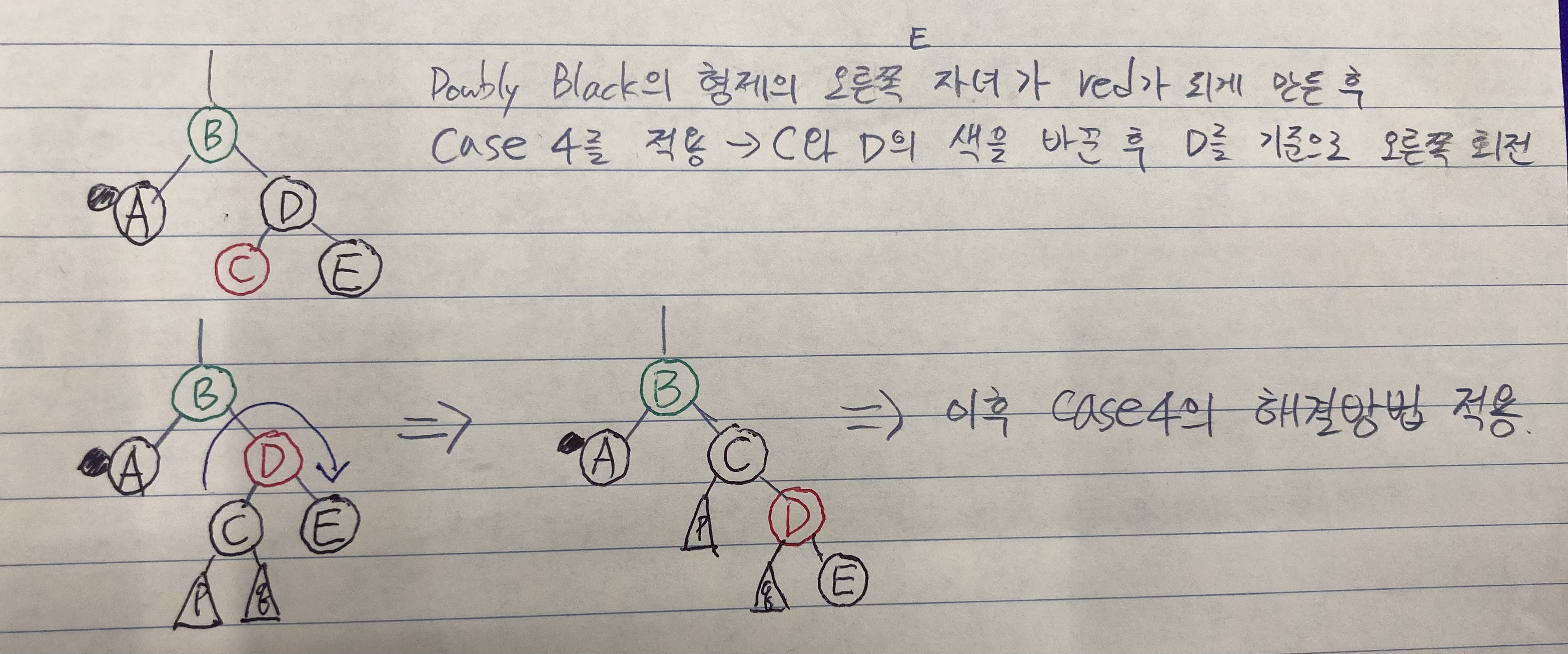
case 3.
doubly black의 오른쪽 형제가 black & 그 형제의 왼쪽 자녀가 red, 오른쪽 자녀는 black일 때
doubly black의 형제의 오른쪽(왼쪽) 자녀를 red가 되게 만들어서 case 4를 적용할 수 있게 만든다.
- doubly black의 형제가 black, 그 형제의 두 자녀 모두 black
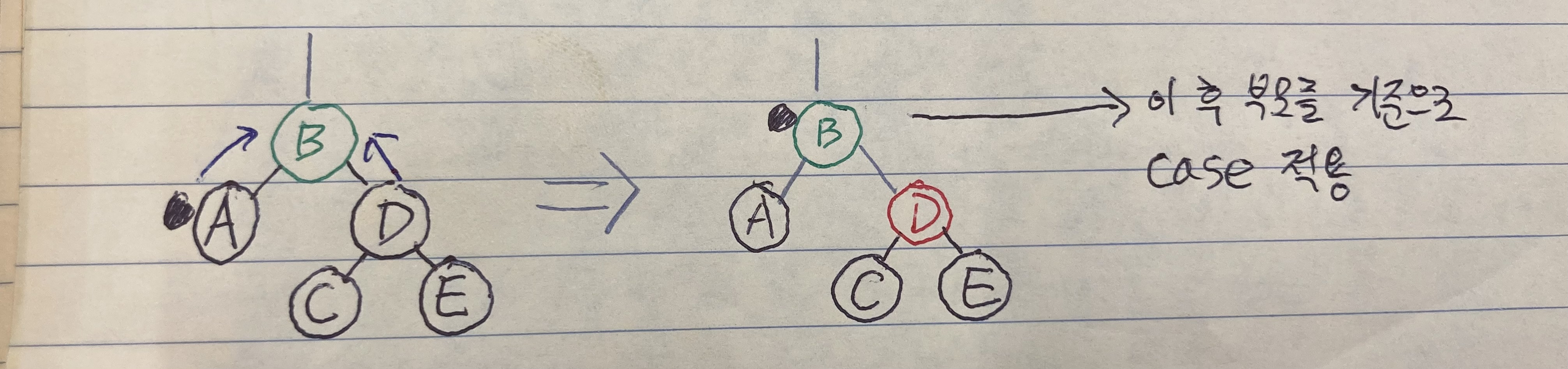
case 2.
doubly black의 형제가 black, 그 형제의 두 자녀 모두 black일 때
doubly black과 그 형제의 black을 모아서 부모에게 전달한 후 부모가 extra black을 해결하도록 위임한다.
- doubly black의 형제가 red
doubly black의 형제를 black으로 만든 후 case 2, 3, 4를 적용한다.
case 1.
doubly black의 오른쪽(왼쪽)형제가 red일 때, 부모와 형제의 색을 바꾸고
부모를 기준으로 왼쪽(오른쪽)으로 회전한 뒤 doubly black을 기준으로 case 2, 3, 4 중 하나를 적용.
실제 코드는 다음과 같다.
void rbtree_delete_fixup(rbtree *t, node_t *target) {
while(target != t -> root && target -> color == RBTREE_BLACK) {
//left child
if (target == target -> parent -> left) {
node_t *bro = target -> parent -> right;
//case 1 doubly black의 형제가 red일 때
if (bro -> color == RBTREE_RED) {
bro -> color = RBTREE_BLACK;
target -> parent -> color = RBTREE_RED; //부모와 형제의 색을 바꾸고
left_rotation(t, target -> parent);
bro = target -> parent -> right;
}
//case 2 형제가 black, 형제의 두 자녀 모두 black일 때
if (bro -> left -> color == RBTREE_BLACK && bro -> right -> color == RBTREE_BLACK) {
bro -> color = RBTREE_RED;
target = target -> parent;
} else {
//case 3 오른쪽 형제가 black이고 그 형제의 오른쪽 자녀가 black, 왼쪽 자녀는 red
if(bro -> right -> color == RBTREE_BLACK) {
bro -> left -> color = RBTREE_BLACK;
bro -> color = RBTREE_RED; //bro와 bro -> left의 색을 바꾸고
right_rotation(t, bro); //오른쪽 회전
bro = target -> parent -> right;
}
//case 4 오른쪽 형제가 black이고 그 형제의 오른쪽 자녀가 Red일 때
bro -> color = target -> parent ->color;
target -> parent -> color = RBTREE_BLACK;
bro -> right -> color = RBTREE_BLACK;
left_rotation(t, target -> parent);
target = t -> root; //while 문 종료
}
} else {//right child
node_t *bro = target -> parent -> left;
if (bro -> color == RBTREE_RED) {
//case 1 - reverse 왼쪽 형제가 red일 때
bro -> color = RBTREE_BLACK;
target -> parent -> color = RBTREE_RED;
right_rotation(t, target -> parent);
bro = target -> parent -> left;
}
//case 2 - reverse 형제가 black이고 그 형제의 두 자녀 모두 black일때
if (bro -> right -> color == RBTREE_BLACK && bro -> left -> color == RBTREE_BLACK) {
bro -> color = RBTREE_RED;
target = target -> parent;
} else {
//case 3 - reverse 왼쪽 형제가 black이고 그 형제의 오른쪽 자녀가 red, 왼쪽 자녀가 black일 떄
if (bro -> left -> color == RBTREE_BLACK) {
bro -> right -> color = RBTREE_BLACK;
bro -> color = RBTREE_RED;
left_rotation(t, bro);
bro = target -> parent -> left;
}
//case 4 - reverse 왼쪽 형제가 black이고 그 형제의 왼쪽 자녀가 red, 오른쪽 자녀가 black일 떄
bro -> color = target -> parent -> color;
target -> parent -> color = RBTREE_BLACK;
bro -> left -> color = RBTREE_BLACK;
right_rotation(t, target -> parent);
target = t -> root;
}
}
}
target -> color = RBTREE_BLACK; //root의 색깔은 black.
}
int rbtree_erase(rbtree *t, node_t *target) {
color_t delete_soon_color = target -> color; //삭제할 색깔 기억
node_t *replace; //target을 교체할 replace 노드
if (target -> left == t -> nil) { //타겟의 left가 없다면
replace = target -> right; //extra black이 담길 자리
rbtree_transplant (t, target, target -> right);
} else if (target -> right == t -> nil) { //타겟의 right가 없다면
replace = target -> left; //extra black이 담길 자리
rbtree_transplant (t, target, target -> left);
} else { //target의 자식이 둘일 때
node_t *successor = target -> right; //successor = target의 오른쪽 subtree내에서 가장 작은 값
while(successor -> left != t -> nil) { //target의 오른쪽 subtree에서 가장 작은 값을 찾는 반복문
successor = successor -> left;
}
delete_soon_color = successor -> color; //삭제할 색깔을 successor의 색으로 변경
replace = successor -> right; //extra black이 담길 자리
if (successor -> parent == target) {
replace -> parent = successor;
} else {
rbtree_transplant(t, successor, successor -> right);
successor -> right = target -> right;
successor -> right -> parent = successor;
}
rbtree_transplant(t, target, successor);
successor -> left = target -> left;
successor -> left -> parent = successor;
successor -> color = target -> color;
}
if (delete_soon_color == RBTREE_BLACK) { //삭제한 색깔이 black 이었다면 조정이 필요함
rbtree_delete_fixup(t, replace);
}
free(target);
return 0;
}이하는 RB tree의 전체 코드이다.
#include "rbtree.h"
#include <stdlib.h>
rbtree *new_rbtree(void) {
rbtree *p = (rbtree *)calloc(1, sizeof(rbtree));
//새로운 트리 생성
p -> nil = (node_t*)malloc(sizeof(node_t)); //센티넬 노드
p -> nil -> color = RBTREE_BLACK; //NIL노드의 색은 항상 black
p -> nil -> parent = p -> nil -> left = p -> nil -> right = p -> nil; //대입 연산은 항상 우에서 좌 순서로
//p의 부모노드도, 왼쪽 노드도, 오른쪽 노드도 모두 nil(NULL)
p -> root = p -> nil;
//root 포인터도 nil로 초기화
return p;
}
void delete_node(rbtree *t, node_t*x) {
if (x == t -> nil) {
return;
}
delete_node(t, x -> left); //왼쪽 자녀 노드에 delete_node 재귀
delete_node(t, x -> right); //오른쪽 자녀 노드에 delete_node 재귀
free(x); // x가 동적으로 점유하던 메모리 반환 (후위순회 방식 왼쪽 -> 오른쪽 -> 루트)
}
void delete_rbtree(rbtree *t) {
if (t -> root != t -> nil) { //root노드에 대해서 delete_node 실행
delete_node(t, t->root);
}
free(t -> nil); //nil에 동적으로 할당하던 메모리 반환
free(t); //rbtree 자체도 반환
}
void right_rotation(rbtree *t, node_t *x) {
//1. target의 left로 y를 선언
node_t *y = x -> left;
//2. y의 오른쪽 서브트리를 target의 왼쪽 서브트리로 옮김
x -> left = y -> right;
//3. y의 오른쪽 노드가 NIL이 아니라면, y의 오른쪽 노드의 부모를 target으로 변경
if (y -> right != t -> nil) {
y -> right -> parent = x;
}
//4. y의 부모 노드를 target의 부모 노드로 설정
y -> parent = x -> parent;
//5. target의 부모 노드가 NIL 이라면 (target이 root인 경우) t 구조체의 root를 y로 설정 (target의 자리를 y가 차지)
if (x -> parent == t -> nil) {
t -> root = y;
//6. target이 target 부모 노드의 왼쪽이면, target 부모의 왼쪽을 y로 설정 (target의 자리를 y가 차지)
} else if (x == x -> parent -> left) {
x -> parent -> left = y;
//7. target이 target 부모 노드의 오른쪽이면, target 부모의 오른쪽을 y로 설정 (target의 자리를 y가 차지)
} else {
x -> parent -> right =y;
}
//8. target을 y의 오른쪽으로 설정
y -> right = x;
//9. target의 부모를 y로 설정
x -> parent = y;
}
void left_rotation(rbtree *t, node_t *x) { //right rotation의 반대
node_t *y = x->right;
x->right = y->left;
if (y->left != t->nil) {
y->left->parent = x;
}
y->parent = x->parent;
if (x->parent == t->nil) {
t->root = y;
} else if (x == x->parent->left) {
x->parent->left = y;
} else {
x->parent->right = y;
}
y -> left = x;
x -> parent = y;
}
void rbtree_insert_fixup(rbtree *t, node_t *z) {
node_t *y;
//삽입된 노드의 부모가 black일 경우 아무 문제 없다.
while (z -> parent ->color ==RBTREE_RED) {
//z의 부모가 조부모의 왼쪽 서브트리인 경우
if (z -> parent == z -> parent -> parent -> left) {
//y는 z의 uncle 노드
y = z -> parent -> parent -> right;
//case.1 삽입된 노드 z의 삼촌 y가 red 인 경우 (parent 도 red, uncle도 red)
if (y -> color == RBTREE_RED) {
z -> parent -> color = RBTREE_BLACK; //부모의 색을 black으로
y -> color = RBTREE_BLACK; //uncle의 색도 black으로
z -> parent -> parent -> color = RBTREE_RED; //조부모의 색을 red로 변경
z = z -> parent -> parent;
}
//case.2 삽입된 노드 z의 삼촌 y가 black이며 z가 오른쪽 자식인 경우 (triangle 모양)
else {
if (z == z -> parent -> right) {
z = z -> parent;
left_rotation(t, z);
} //triangle 모양일때는 left rotation과 (아래에서)right rotation 을 실시한다.(2회전)
//case.3 삽입된 노드 z의 삼촌 y가 black이며 z가 왼쪽 자식인 경우 (linear 모양)
z -> parent -> color = RBTREE_BLACK;
z -> parent -> parent -> color = RBTREE_RED;
right_rotation(t, z -> parent -> parent);
//linear 모양일때는 right_rotation만 실시한다. (1회전)
}
} else { //z의 부모가 조부모의 오른쪽 서브 트리일 경우
y = z -> parent -> parent ->left; //삼촌은 왼쪽에 있다.
//case.4 삽입된 노드 z의 삼촌 y가 red인 경우 (parent 도 red, uncle도 red)
if (y->color == RBTREE_RED) {
z->parent->color = RBTREE_BLACK;
y->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
z = z->parent->parent;
}
//case.5 z의 삼촌 y가 black이며 z가 왼쪽 자식인 경우 (triangle 모양)
else {
if (z == z -> parent -> left) {
z = z -> parent;
right_rotation(t, z);
}
//case.6: z의 삼촌 y가 black이며 z가 오른쪽 자식인 경우 (linear 모양)
z -> parent -> color = RBTREE_BLACK;
z -> parent -> parent -> color = RBTREE_RED;
left_rotation(t, z -> parent -> parent);
}
}
}
t -> root -> color = RBTREE_BLACK; //root는 black
}
node_t *rbtree_insert(rbtree *t, const key_t key) {
node_t *y = t -> nil;
node_t *x = t -> root;
node_t *z = (node_t*) malloc(sizeof(node_t)); //z를 동적할당
z -> key = key; //z에 key 대입
while (x != t -> nil) {
y = x;
if (z -> key < x -> key) { //z의 key가 x의 key 보다 작다면
x = x -> left; //왼쪽으로
} else { // 작지 않으면(같은 경우 포함)
x = x -> right; //오른쪽으로
}
}
z -> parent = y;
if (y == t -> nil) { //z의 부모가 없다면 z가 root다.
t->root = z;
} else if (z -> key < y -> key) {
y -> left = z;
} else {
y -> right = z;
}
z -> left = t -> nil;
z -> right = t -> nil; //z의 자식들이 모두 NIL (z는 가장 아래)
z -> color = RBTREE_RED;
rbtree_insert_fixup(t, z);
return t -> root;
}
node_t *rbtree_find(const rbtree *t, const key_t key) {
if (t -> root == t -> nil) { // 트리에 노드가 없다면
return NULL;
}
node_t *temp = t -> root; //임시값 temp를 root로 설정
while (temp != t -> nil) { //temp가 nil까지 내려가지 않았다면
if (temp -> key == key) {
return temp;
}
if (temp -> key > key) { //인수 key가 temp보다 클 때
temp = temp -> left; //temp를 왼쪽으로 한칸 내려서 비교
} else { //인수 key가 temp보다 작을 때
temp = temp -> right; //temp를 오른쪽으로 한칸 내려서 비교
}
}
return NULL; //nil 까지 내려갔어도 못찾았으면 return NULL
}
node_t *rbtree_min(const rbtree *t) {
if (t -> root == t -> nil) { // 트리에 노드가 없다면
return NULL;
}
node_t* temp_parent = t -> nil;
node_t* temp_child = t -> root; //root위에 temp라는 가상의 노드를 만든다.
while (temp_child != t -> nil) { //temp_child가 NIL로 갈 때 까지 내려가기
temp_parent = temp_child;
temp_child = temp_child -> left; //최소니까 왼쪽으로 내려가기
}
return temp_parent;
}
node_t *rbtree_max(const rbtree *t) {
if (t -> root == t -> nil) { // 트리에 노드가 없다면
return NULL;
}
node_t* temp_parent = t -> nil;
node_t* temp_child = t -> root; //root위에 temp라는 가상의 노드를 만든다.
while (temp_child != t -> nil) { //temp_child가 NIL로 갈 때 까지 내려가기
temp_parent = temp_child;
temp_child = temp_child -> right; //최대니까 오른쪽으로 내려가기
}
return temp_parent;
}
void rbtree_transplant(rbtree *t, node_t *from, node_t *to){
if (from -> parent == t -> nil){ //from 이 root인 경우
t -> root = to;
} else if (from == from -> parent -> left) { //from이 왼쪽 노드인 경우
from -> parent -> left = to;
} else { //from이 오른쪽 노드인 경우
from -> parent -> right = to;
}
to -> parent = from -> parent; //to와 from의 부모를 이음
return;
}
void rbtree_delete_fixup(rbtree *t, node_t *target) {
while(target != t -> root && target -> color == RBTREE_BLACK) {
//left child
if (target == target -> parent -> left) {
node_t *bro = target -> parent -> right;
//case 1 doubly black의 형제가 red일 때
if (bro -> color == RBTREE_RED) {
bro -> color = RBTREE_BLACK;
target -> parent -> color = RBTREE_RED; //부모와 형제의 색을 바꾸고
left_rotation(t, target -> parent);
bro = target -> parent -> right;
}
//case 2 형제가 black, 형제의 두 자녀 모두 black일 때
if (bro -> left -> color == RBTREE_BLACK && bro -> right -> color == RBTREE_BLACK) {
bro -> color = RBTREE_RED;
target = target -> parent;
} else {
//case 3 오른쪽 형제가 black이고 그 형제의 오른쪽 자녀가 black, 왼쪽 자녀는 red
if(bro -> right -> color == RBTREE_BLACK) {
bro -> left -> color = RBTREE_BLACK;
bro -> color = RBTREE_RED; //bro와 bro -> left의 색을 바꾸고
right_rotation(t, bro); //오른쪽 회전
bro = target -> parent -> right;
}
//case 4 오른쪽 형제가 black이고 그 형제의 오른쪽 자녀가 Red일 때
bro -> color = target -> parent ->color;
target -> parent -> color = RBTREE_BLACK;
bro -> right -> color = RBTREE_BLACK;
left_rotation(t, target -> parent);
target = t -> root; //while 문 종료
}
} else {//right child
node_t *bro = target -> parent -> left;
if (bro -> color == RBTREE_RED) {
//case 1 - reverse 왼쪽 형제가 red일 때
bro -> color = RBTREE_BLACK;
target -> parent -> color = RBTREE_RED;
right_rotation(t, target -> parent);
bro = target -> parent -> left;
}
//case 2 - reverse 형제가 black이고 그 형제의 두 자녀 모두 black일때
if (bro -> right -> color == RBTREE_BLACK && bro -> left -> color == RBTREE_BLACK) {
bro -> color = RBTREE_RED;
target = target -> parent;
} else {
//case 3 - reverse 왼쪽 형제가 black이고 그 형제의 오른쪽 자녀가 red, 왼쪽 자녀가 black일 떄
if (bro -> left -> color == RBTREE_BLACK) {
bro -> right -> color = RBTREE_BLACK;
bro -> color = RBTREE_RED;
left_rotation(t, bro);
bro = target -> parent -> left;
}
//case 4 - reverse 왼쪽 형제가 black이고 그 형제의 왼쪽 자녀가 red, 오른쪽 자녀가 black일 떄
bro -> color = target -> parent -> color;
target -> parent -> color = RBTREE_BLACK;
bro -> left -> color = RBTREE_BLACK;
right_rotation(t, target -> parent);
target = t -> root;
}
}
}
target -> color = RBTREE_BLACK; //root의 색깔은 black.
}
int rbtree_erase(rbtree *t, node_t *target) {
color_t delete_soon_color = target -> color; //삭제할 색깔 기억
node_t *replace; //target을 교체할 replace 노드
if (target -> left == t -> nil) { //타겟의 left가 없다면
replace = target -> right; //extra black이 담길 자리
rbtree_transplant (t, target, target -> right);
} else if (target -> right == t -> nil) { //타겟의 right가 없다면
replace = target -> left; //extra black이 담길 자리
rbtree_transplant (t, target, target -> left);
} else { //target의 자식이 둘일 때
node_t *successor = target -> right; //successor = target의 오른쪽 subtree내에서 가장 작은 값
while(successor -> left != t -> nil) { //target의 오른쪽 subtree에서 가장 작은 값을 찾는 반복문
successor = successor -> left;
}
delete_soon_color = successor -> color; //삭제할 색깔을 successor의 색으로 변경
replace = successor -> right; //extra black이 담길 자리
if (successor -> parent == target) {
replace -> parent = successor;
} else {
rbtree_transplant(t, successor, successor -> right);
successor -> right = target -> right;
successor -> right -> parent = successor;
}
rbtree_transplant(t, target, successor);
successor -> left = target -> left;
successor -> left -> parent = successor;
successor -> color = target -> color;
}
if (delete_soon_color == RBTREE_BLACK) { //삭제한 색깔이 black 이었다면 조정이 필요함
rbtree_delete_fixup(t, replace);
}
free(target);
return 0;
}
void inorder_search(node_t *root, node_t *nil, key_t *arr, int *index) {
if (root == nil) { // 트리 안에 아무것도 없다면
return;
}
inorder_search(root -> left, nil, arr, index); //중위순회
arr[(*index)++] = root -> key; //배열의 *index++에 key값을 담는다.
inorder_search(root -> right, nil, arr, index); //중위순회
}
int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n) {
int *index = (int *)calloc(1, sizeof(int)); //배열의 index를 가리키는 포인터
inorder_search(t->root, t -> nil, arr, index);
free(index); //메모리 반환
return 0;
}