A3C(Asynchronous Advantage Actor-Critic)

signer do·2024년 8월 27일

강화학습

목록 보기

10/11

A2C 알고리즘은 Episode가 끝날 때까지 기다릴 필요 없이 샘플이 보이는 대로 바로 정책을 update할 수 있게 하고 gradient의 분산을 줄였지만, 여전히 문제점을 가지고 있다. 가장 큰 문제는 policy와 value function을 학습시킬 때 사용되는 sample이 시간적으로 상관되어 있다. 시간의 흐름에 따라 순차적으로 sample을 수집하고, 시간적으로 매우 가까운 sample만 모아서 policy를 update하다보니 상관관계가 커지는 것이다. 이러한 샘플 간의 높은 상관관계는 objective function의 gradient를 편향시키고 학습을 불안정하게 만들 수 있다.
학습 배치(batch)에 있는 서로 유사한 데이터는 신경망을 비슷한 방향으로 update할 것이기 때문이다. 따라서 목적 함수의 향상에 도움이 되는 데이터인지 아닌지에 따라 전체적인 update 방향이 잘못될 수가 있다.
이러한 문제를 개선하기 위해 비동기 A2C(A3C, asynchronous advantage actor-critic) 알고리즘이 등장하게 되었다.

1. Gradient 계산 문제

1.1 Sample 상관관계

Advantage Actor-Critic에서 사용한 Objective Function의 Gradient 식을 다시 써보면 아래와 같다.
$\nabla_\theta J(\theta)=\sum\limits^T_{t=0}(\mathbb{E}_{\mathbf{x}_t\sim p_\theta(\mathbf{x}_t), \mathbf{u}_t\sim\pi_\theta(\mathbf{u}_t|\mathbf{x}_t)}[\nabla_\theta\log \pi_\theta(\mathbf{u}_t|\mathbf{x}_t) A^{\pi_\theta}(\mathbf{x}_t, \mathbf{u}_t)]$

Sampling 기법을 이용하면 Objective Function의 Graident를 아래와 같이 근사적으로 계산할 수 있다.
$\nabla_\theta J(\theta)\approx\sum\limits^T_{t=0}[\cfrac{1}{M}\sum\limits^M_{m=1}\nabla_\theta\log \pi_\theta(\mathbf{u}_t^{(m)}|\mathbf{x}_t^{(m)}) A^{\pi_\theta}(\mathbf{x}_t^{(m)}, \mathbf{u}_t^{(m)})$

$m$ 은 Episode index이며
$M$ 은 Episode 갯수
$t$ 은 시간 step
$T$ 은 Episode가 종료될 때까지 step

한 개의 Episode만 고려하면 Objectvie Function은 근사적으로 아래와 같다.
$\nabla_\theta J(\theta)\approx\sum\limits^T_{t=0}(\nabla_\theta\log \pi_\theta(\mathbf{u}_t|\mathbf{x}_t) A^{\pi_\theta}(\mathbf{x}_t, \mathbf{u}_t))$

batch gradient ascent(배치 경사 상승법)으로 Actor 신경망을 update하려면 다음과 같이 Actor 신경망 parameter $\theta$ 를 반복 계산해야 한다.
$\theta\leftarrow\theta+\alpha\sum\limits^T_{t=0}(\nabla_\theta\log\pi_\theta(\mathbf{u}_t|\mathbf{x}_t) A^\pi_{\theta}(\mathbf{x}_t,\mathbf{u}_t))$

일반적인 미니배치 데이터로 update하려면 무작위로 batch의 data를 섞은 후 다음과 같이 actor 신경망 파라미터 $\theta$ 를 반복 계산해야 한다.
- N개 미니배치 모은 후 update N개 미니배치 모은 후 update, T까지 반복
A2C 알고리즘에서도 미니 배치 데이터로 update하는 것과 유사하게, 1개의 Episode 내에서 일정 시간 $N$ 동안 objective function gradient를 이용해 다음과 같이 parameter를 updae했다.
- for i in range(0,T,N-1)
  - $\theta\leftarrow\theta+\alpha\sum\limits^{i+N-1}_{t=i}(\nabla_\theta\log\pi_\theta(\mathbf{u}_t|\mathbf{x}_t)A^{\pi_\theta}(\mathbf{x}_t, \mathbf{a}_t))$

위의 update 방식은 형식적으로 일반적인 일반적인 mini batch 데이터를 이용해 update한 것 같지만, 일반적인 방법과 다르다.
A2C 알고리즘에서 agent가 policy $\pi_{\theta_1}$ 으로 일정 시간 step $N$ 동안 수집한 $N$ 개의 sample( $\mathbf{x}_i, \mathbf{u}_i,r(\mathbf{x}_i,\mathbf{a}_i), \mathbf{x}_{i+1})$ 을 얻은 후 policy $\pi_{\theta_2}$ 로 update한다.
이 update된 policy는 이전 policy와는 다른 새로운 policy가 된다. 다시 새로운 policy $\pi_{\theta_3}$ 로 일정 시간 step $N$ 동안 수집한 $N$ 개의 sample로 policy를 다시 update하는 과정을 반복한다.

SGD(Stochastic Gradient Descent)를 이용한 최적화 방법의 기본 가정은 training data가 독립적이고 동일한 분포(independent identical distribution)을 가진 sample이어야 한다.
위와 같은 방식 update 방식은 data가 독립적이지 않다.
agent가 env와 상호작용하면서 순차적으로 data를 얻기 때문에 일정 시간 step $N$ 동안 수집한 $N$ 개의 sample $(\mathbf{x}_i, \mathbf{u}_i, r(\mathbf{x}_i, \mathbf{u}_i), \mathbf{x}_{i+1})$ 도 시간 상 순차적인 data이므로 강한 상관관계가 있다고 할 수 있다. 또한 data는 동일한 분포를 가진 sample이라고 말할 수 없다. 왜냐하면, actor 신경망의 parameter를 update하여 새로운 policy로 얻은 데이터는 이전 data와는 다른 확률 분포를 가질 것이다. 기본적으로 강화학습의 순차적인 학습과정에서 얻는 data는 독립적이고 동일한 분포라는 가정을 충족시키기 어렵다.

data간 상관관계 문제를 해결하기 위해 DQN 네트워크에서 agent의 experience(data)를 바로 학습에 사용하지 않고 replaybuffer라는 곳에 저장해두고 buffer에 어느 정도 이상 data가 모이면 buffer에서 랜덤으로 batch만큼 sampling해서 학습에 이용한다. 랜덤으로 data를 추출하기 때문에 mini batch가 순차적인 data로 구성되지 않으므로 data 사이의 상관관계를 많이 줄일 수 있다. 또한 buffer가 차면 오래된 data를 먼저 제거하는 방식으로 최근 policy로 발생시킨 data 위주로 학습이 진행되도록 했다.

이와 같이 replay buffer를 이용해 학습이 가능한 이유는 DQN이 off-policy 방법이기 때문이다. 하지만 A2C는 on-policy 방법이기 때문에 이러한 replay buffer 방법을 사용할 수가 없다. on-policy 방법은 다른 policy로 만든 data를 이용해 현재 policy를 update할 수 없기 때문이다.

on-policy 방법인 A2C에서 데이터 간의 상관관계를 줄이기 위한 방법을 찾기 위해 다시 sampling 기법을 이용한 objective function의 gradient의 근사식을 살펴보자.
$\nabla_\theta J(\theta)\approx\sum\limits^T_{t=0}[\cfrac{1}{M}\sum\limits^M_{m=1}\nabla_\theta\log \pi_\theta(\mathbf{u}_t^{(m)}|\mathbf{x}_t^{(m)}) A^{\pi_\theta}(\mathbf{x}_t^{(m)}, \mathbf{u}_t^{(m)})$
$=\cfrac{1}{M}\sum\limits^M_{m=1}\sum\limits^T_{t=0}\nabla_\theta\log \pi_\theta(\mathbf{u}_t^{(m)}|\mathbf{x}_t^{(m)}) A^{\pi_\theta}(\mathbf{x}_t^{(m)}, \mathbf{u}_t^{(m)})$
$\approx\cfrac{1}{M}\sum\limits^M_{m=1}\sum\limits^{t+N-1}_{i=t}(\nabla_\theta\log \pi_\theta(\mathbf{u}_i^{(m)}|\mathbf{x}_i^{(m)}) A^{\pi_\theta}(\mathbf{x}_i^{(m)}, \mathbf{u}_i^{(m)}))$

위 식에 의하면 gradient를 계산하기 위해서 동일한 policy $\pi_\theta$ 로 여러 개의 독립적인 episode를 발생시킨 후 각각의 episode에서 일정 시간스텝 동안( $N$ )의 데이터로 log-policy gradient와 Advantage 곱을 계산해 모두 더하고 Episode 평균을 내면 된다.

동일한 정책 $\pi_\theta$ 로 여러 개의 독립적인 Episode를 발생시키는 방법은 실제 세계에서 구현한 것이 바로 multi-agent를 병렬적으로 운용하여 각 agent가 각자 독립적인 env와 상호작용하면서 data를 수집하는 것이다. 이렇게 하면 각각의 agent가 서로 다른 state, reward, state-transition 등을 경험하면서 data를 모으기 때문에 학습 데이터의 연관성을 깰 수 있다.

multi-agent를 병렬적으로 운용함에 있어서 2가지 서로 다른 방식을 고려해 볼 수 있다.

1.2 동기적 Actor-Critirc

여러개의 agent가 수집한 data를 동일한 시간에 모두 모아서 한꺼번에 모든 agent의 policy와 value fucntion을 update하는 동기적인 actor-critic 방법이다. 모든 agent가 동일한 policy를 가지고 data를 만들고 이를 이용해 policy를 동시에 update한다.

1.3 비동기적 Actor-Critic

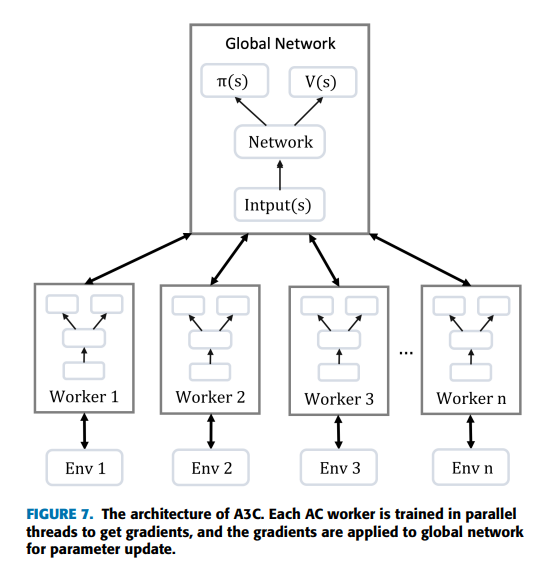
global 신경망과 worker라고 불리는 여러 개의 agent가 있다. global 신경망과 worker는 각자의 actor 신경망과 critic 신경망을 갖는다. worker가 일정시간 수집한 정보를 global 신경망에 전달하면 global 신경망은 자신의 actor와 critic 신경망을 update하고 update된 신경망 parameter를 해당 worker에 복사한다. 이러한 과정은 정해진 시간에 모든 워커가 일제히 update를 수행하는 것이 아니라, worker마다 각자의 시간에 비동기적으로 수행한다.

비동기 방식에는 어떤 정보를 global 신경망에 전달하고 objective function의 gradient를 어디서 계산하는지에 따라 2가지 접근 방법이 있다.

1.3.1 gradient parallelism

worker가 수집한 $N$ 개의 sample $(\mathbf{x}_i, \mathbf{u}_i, r(\mathbf{x}_i, \mathbf{u}_i), \mathbf{x}_{i+1})$ 로 자신의 gradient를 계산하고 그 결과를 global 신경망에 전달하는 것. global 신경망이 이를 이용해 자신의 신경망을 update하고 update된 신경망을 agent에 복사하는 방식
→ gradient의 계산을 worker에게 맡김으로써 global 신경망의 계산량을 줄일 수 있기 때문에 worker의 수를 확장하기가 비교적 쉽다.

1.3.2 data parallelism

worker가 $N$ 개의 sample $(\mathbf{x}_i, \mathbf{u}_i, r(\mathbf{x}_i, \mathbf{u}_i), \mathbf{x}_{i+1})$ 을 global 신경망에 전달하면 이 데이터를 이용해 목적함수 gradient를 계산한 후 global 신경망을 update하고 update된 신경망을 agent에 복사하는 방식
→ gradient 계산과 신경망 update를 global 신경망이 전담하고 worker는 데이터 수집만 수행.

위와 같이 다수의 worker agent를 병렬적으로 운용하며 비동기적으로 global actor, critic 신경망을 update하는 방법을 A3C라고 한다.

1.2 n-step 가치 추정

objective function의 gradient를 계산할 때 advantage를 bias 없이 작은 variance 값을 갖도록 추정하는 것이 중요하다. A2C 알고리즘에서 value 함수를 근사하는 함수인 $V_\phi(\mathbf{x}_t)$ 를 다음과 같이 1-step 관계식을 이용해 추정
$V_\phi(\mathbf{x}_t)\approx r(\mathbf{u}_t,\mathbf{r}_t)+\gamma V_\phi(\mathbf{x}_{t+1})$

advantage도 다음과 같이 1-step 관계식을 이용해 근사적으로 계산
$A_\phi(\mathbf{x}_t, \mathbf{u}_t)\approx r(\mathbf{x}_t,\mathbf{u}_t)+\gamma V_\phi(\mathbf{x}_{t+1})-V_\phi(\mathbf{x}_t)$
1-step 관계식을 이용하면 advantage 추정값의 variance는 작은 반면, state value function의 추정 정확도에 따라 advantage 추정값에 큰 bias가 있을 수 있다.
반면에, 무한 구간에서 action-value function 정의에 따라 몬테카를로 방식으로 한개의 Episode에서 아래 식과 같이 Advantage를 계산한다면,
$A_\phi(\mathbf{x}_t)\approx \sum\limits_{k=t}^{\infty}\gamma ^{k-t}r(\mathbf{x}_k,\mathbf{r}_k)-V_\phi(\mathbf{x}_t)$
bias는 작지만, 큰 분산을 갖게 된다. 수많은 step의 state와 action에서 reward가 계속 누적되기 때문

이 양극단의 중간을 취하면서 bias와 variance를 적절히 조절할 수 있는 방식이 바로 다음과 같은 n-step value-function 추정과 advantage 계산법

$V_\phi(\mathbf{x}_t)\approx r(\mathbf{x}_t, \mathbf{u}_t)+\gamma r(\mathbf{x}_{t+1}, \mathbf{u}_{t+1})+\cdots+\gamma^{n-1}r(\mathbf{x}_{t+n-1}, \mathbf{u}_{t+n-1})+\gamma^n V_\phi(\mathbf{x}_{t+n})$

$A_\phi(\mathbf{x}_t)\approx r(\mathbf{x}_t, \mathbf{u}_t)+\gamma r(\mathbf{x}_{t+1}, \mathbf{u}_{t+1})+\cdots+\gamma^{n-1}r(\mathbf{x}_{t+n-1}, \mathbf{u}_{t+n-1})+\gamma^n V_\phi(\mathbf{x}_{t+n})-V_\phi(\mathbf{x}_t)$
$=\sum\limits_{k=t}^{t+n-1}\gamma^{k-t}r(\mathbf{x}_k, \mathbf{u}_k)+\gamma^nV_\phi(\mathbf{x}_{t+n})-V_\phi(\mathbf{x}_t)$

n이 크면 advatange의 추정값의 분산은 커지고 편향이 작아지는 반면, n이 작으면 분산은 작아지고 편향이 커질 수 있다. 따라서 A3C 알고리즘에서는 n-step value function 추정과 advantage 계산 방법을 도입해 variance와 bias를 상대적으로 조절하도록 했다.

2. A3C 알고리즘

2.1 gradient 병렬화 방식의 비동기 Actor-Critic

각각의 worker는 자신의 신경망 parameter의 gradient를 계산해 global 신경망으로 보내고, global 신경망은 worker의 gradient를 사용해 자신의 신경망 parameter를 update.
각각의 worker가 그들 env와 상호작용하여 수집한 data를 이용해 global 신경망은 끊임없이 update된다.