강화학습
1.DQN(Deep Q-Network) - Experience Replay
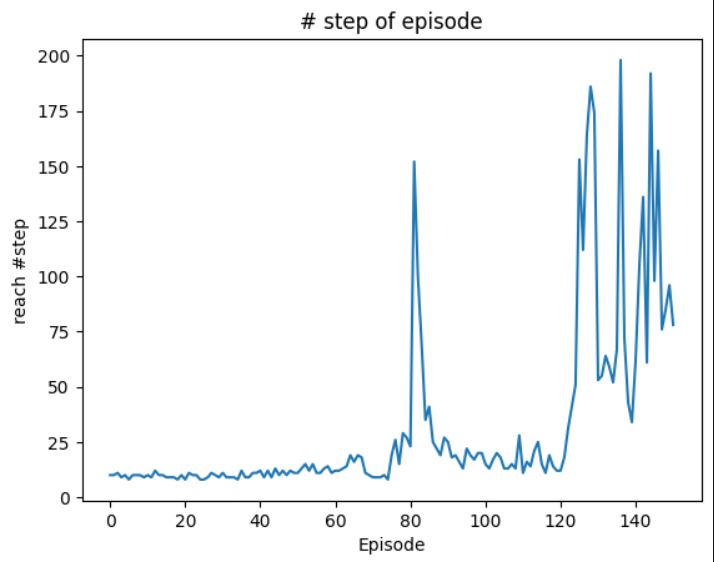
1. Replay method의 처리 개요 저장된 transition 수 확인 저장된 transition 수가 미니배치 크기보다 작으면 처리 중단 미니 배치 생성 memory 객체에서 랜덤으로 미니배치 크기와 같은 개수의 transition 추출 각 상태 변수 미
2.DDQN(Dual Deep Q-Network) 파이토치로 구현하기
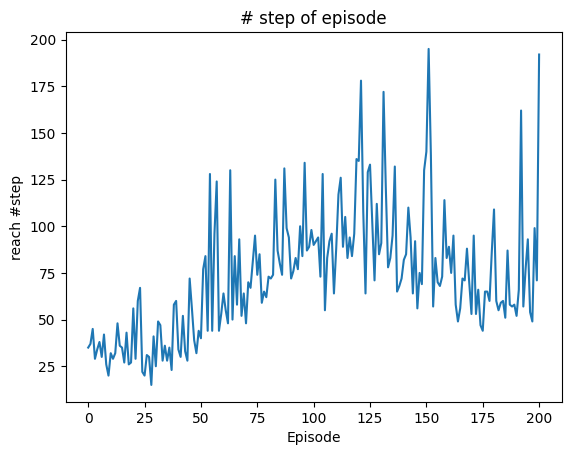
2. DDQN 코드 구현 2.1 라이브러리 포함하기 2.2 state 변수 설정 2.3 상수 정의 2.4 ReplayMemory 구현 2.5 DDQN 알고리즘 구현 2.6 Agent 정의 2.7 Environment 정의 0 Episode: Fini
3.Dueling Network with DDQN 파이토치로 구현하기
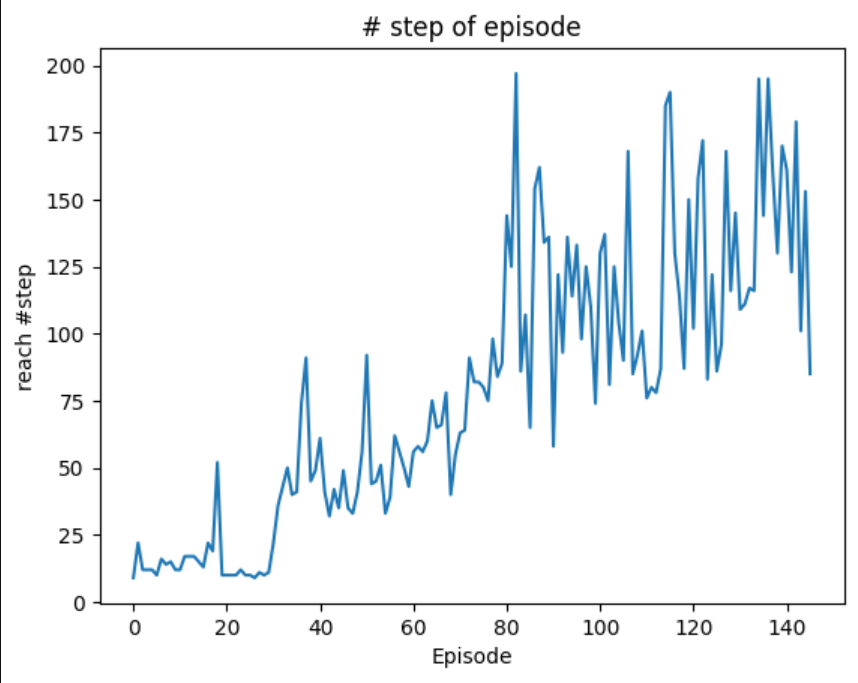
Advantage 함수 $A(s, →)=Q(s, →)-V(s)$ Advantage 함수 도입 의도 task의 action value function Q는 어떤 action을 취하든 받게 되는 할인 총 보상이 상태 s에 의해서만 결정되는 면이 있다. > Ex) 상태 s가
4.마르코프 결정 프로세스 상세 설명

1. 정의 1.1 마르코프 결정 프로세스(MDP) state( $\mathbf{x}t$ ), State Transition Probability Density Function($p$)와 행동($\mathbf{a}t$), reward function($r(\mathbf{
5.벨만 방정식과 벨만 최적 방정식

Bellman Equation은 현재 state의 value와 다음 t+1 시간의 state의 value와의 관계를 나타낸다.value function은 state가 입력값이면서 time-variant 함수이다.$V^{\\pi}(\\mathbf{x}t)=\\mathbb
6.Prioritized Experience Replay 구현하기
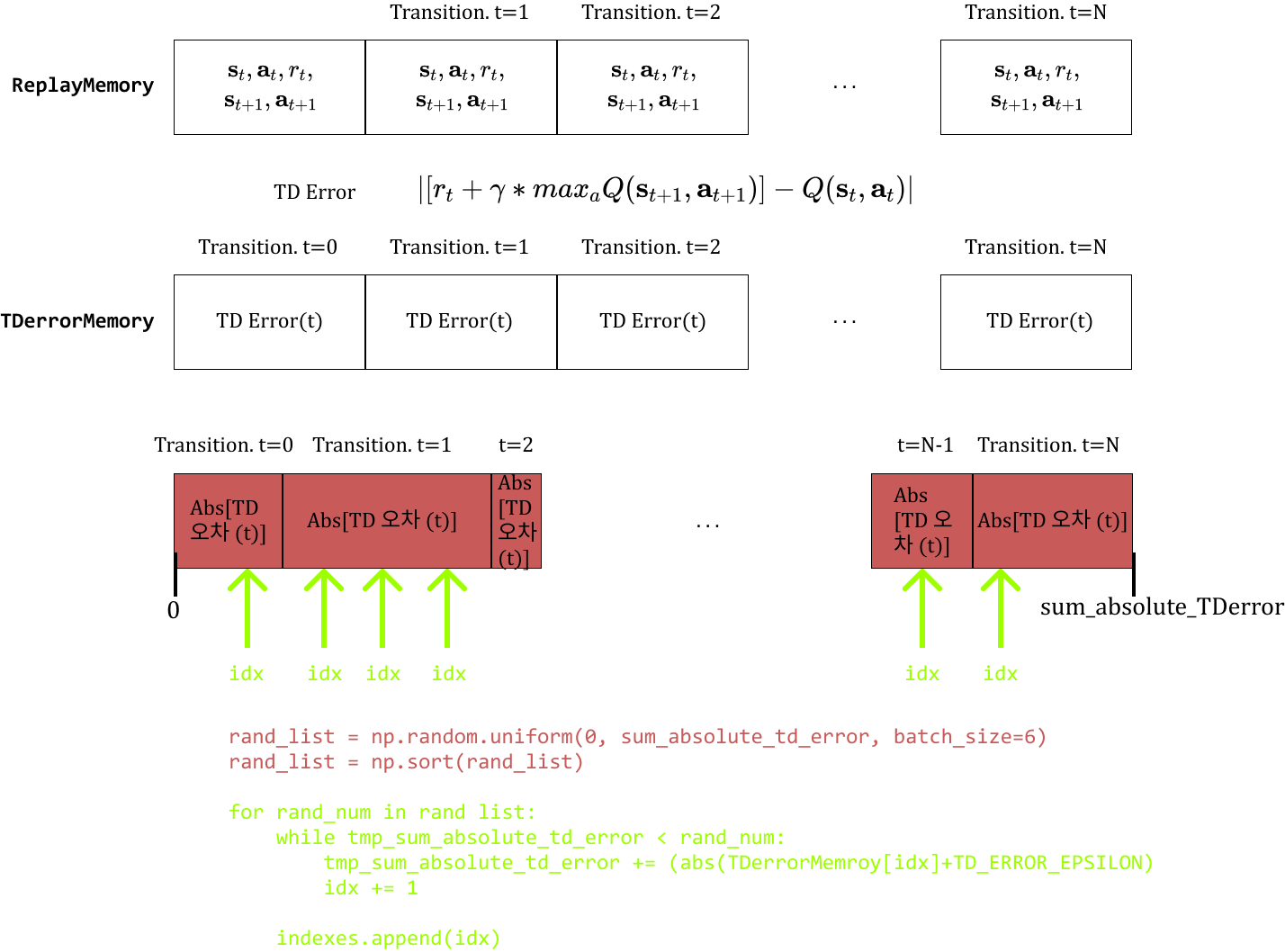
Prioritized Experience Replay Q-러닝이 제대로 지나가지 않은 state의 transition을 우선적으로 학습시키는 기법. 우선순위를 매기는 기준은 Value 함수의 벨만 방정식의 절댓값 오차. $Error = |R(t+1)+\gamma*ma
7.Policy Gradient

1. Objective Function(목적함수) 강화학습의 목표는 return 값의 기댓값으로 이루어진 $J$(목적함수)를 최대로 만드는 정책($\pi(\mathbf{xt|at})$) 구하는 것 Policy가 Parameter화된 것이 $\pi{\theta}(\mat
8.REINFORCE 알고리즘
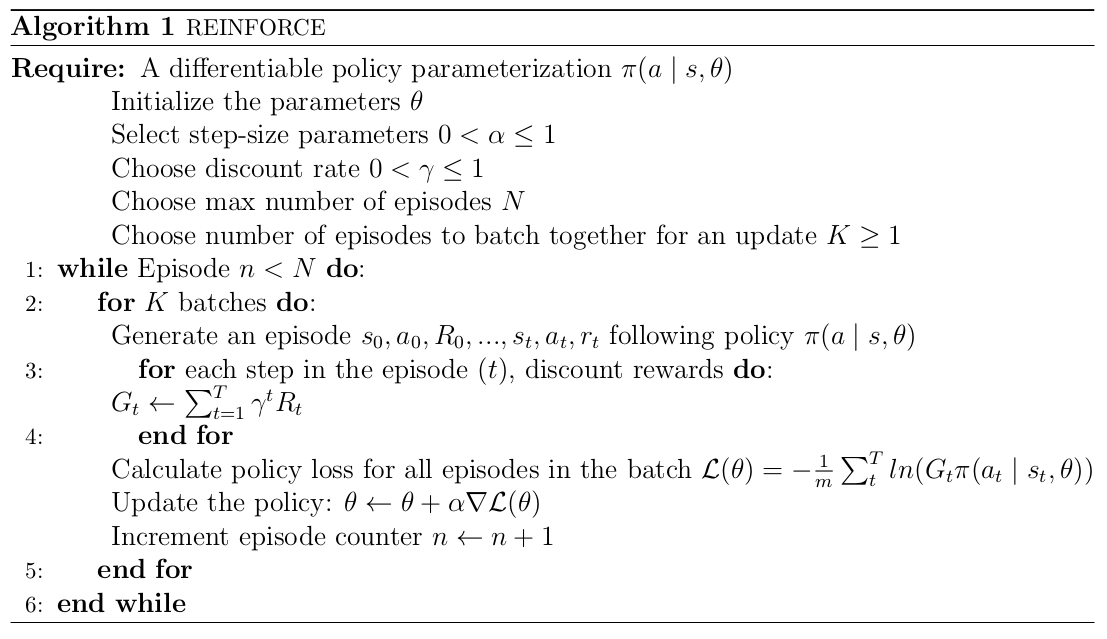
Policy Gradient를 실제 적용하는 데 있어서 trajectory($\\tau$)상의 기댓값 $\\mathbb{E}{\\tau\\ \\sim p\\theta(\\tau)}.$는 sample(policy를 실제로 실행해서 나온 episode)을 이용해 추정할 수
9.A2C(Advantage Actor-Critic)

REINFORCE 알고리즘의 단점은 policy를 update하기 위해서 Episode가 끝날 때까지 기다려야 하고, gradient의 분산이 매우 크다. A2C는 REINFORCE를 일부 고쳐 성능을 훨씬 능가했다. Asynchronous Methods for De
10.A3C(Asynchronous Advantage Actor-Critic)

A2C 알고리즘은 Episode가 끝날 때까지 기다릴 필요 없이 샘플이 보이는 대로 바로 정책을 update할 수 있게 하고 gradient의 분산을 줄였지만, 여전히 문제점을 가지고 있다. 가장 큰 문제는 policy와 value function을 학습시킬 때 사용되
11.PPO 알고리즘

1. Background A2C 알고리즘은 REINFORCE 알고리즘의 아래 2가지 단점을 개선했다. Monte-Carlo update 문제 objective function의 분산이 큰 점 하지만 A2C도 여전히 on-policy라는 단점이 있음. policy를 u