REINFORCE 알고리즘

Policy Gradient를 실제 적용하는 데 있어서 trajectory($\tau$)상의 기댓값 $\mathbb{E}_{\tau\ \sim p_\theta(\tau)}[.]$는 sample(policy를 실제로 실행해서 나온 episode)을 이용해 추정할 수 밖에 없다.
기댓값 $\mathbb{E}_{\tau \sim p_\theta(\tau)}[.]$는 Episode를 M개만큼 sampling해서 Episode 평균을 이용해서 근사적으로 계산.

$\mathbb{E}_{\tau \sim p_\theta(\tau)}[.]\approx \cfrac{1}{M}\sum^M_{m=1}\ [.]$

근사하는 경우 Gradient of Objective Function은 다음과 같이 추정.
$\nabla_\theta J(\theta) \approx \cfrac{1}{M} \sum^M_{m=1}[\sum^T_{t=0}{\nabla_\theta\ log\ \pi_\theta(\mathbf{a_t^{(m)}|x_t^{(m)}) }}(\sum^T_{k=t}\gamma^{k-t}*r(\mathbf{x_k^{(m)}, a_k^{(m)}}))]$

오른쪽 소괄호항은 t=k부터 에피소드 종료 T까지 받을 수 있는 reward 합($G_t$)이다.
$\nabla_\theta J(\theta) \approx \cfrac{1}{M} \sum^M_{m=1}[\sum^T_{t=0}{\nabla_\theta\ log\ \pi_\theta(\mathbf{a_t^{(m)}|x_t^{(m)}) }}*G^{(m)}_t]$

여기서 $G_t^{(m)}$은 $\theta$의 함수가 아니므로
$=\nabla_\theta\ \cfrac{1}{M} \sum^M_{m=1}[\sum^T_{t=0}{\ log\ \pi_\theta(\mathbf{a_t^{(m)}|x_t^{(m)}) }}*G^{(m)}_t]$

매번 Episode를 M개만큼 생성하고 $J(\theta)$가 증가하는 방향으로 $\theta$를 update(Policy Gradient update)를 할 수 있지만,
한 개의 Episode마다 Policy를 update할 수 있다.

1. loss function

parameter($\theta$)로 표현된 policy($\pi_\theta$)를 신경망으로 구성할 때,
한 개의 Episode의 loss 함수는
$loss=-\sum^T_{t=0}(log\ \pi_\theta(\mathbf{a}_t^{(m)}|\mathbf{x}_t^{(m)})*G_t^{(m)})$

$\theta \approx \theta - \alpha \nabla_\theta\sum^T_{t=0}(log\ \pi_\theta(\mathbf{a}_t^{(m)}|\mathbf{x}_t^{(m)})*G_t^{(m)})$

loss함수는 신경망 학습동안 최소화될 값. 신경망은 최소화하도록 parameter가 update되는 반면, policy gradient는 objective function을 최대로 해야하기 때문

loss 함수는 이진분류 문제에서 참값이 항상 1인 cross entropy에 return($G_t$)를 곱한 형태.
$G_t$를 크게 받은 policy를 통한 Episode는 Gradient of objective function 계산 시 더 큰 영향을 끼친다.
반대로, $G_t$를 작게 받은 policy를 통한 Episode는 Gradient 계산 시 작은 영향을 끼쳐서, 점진적으로 policy를 개선한다.

---

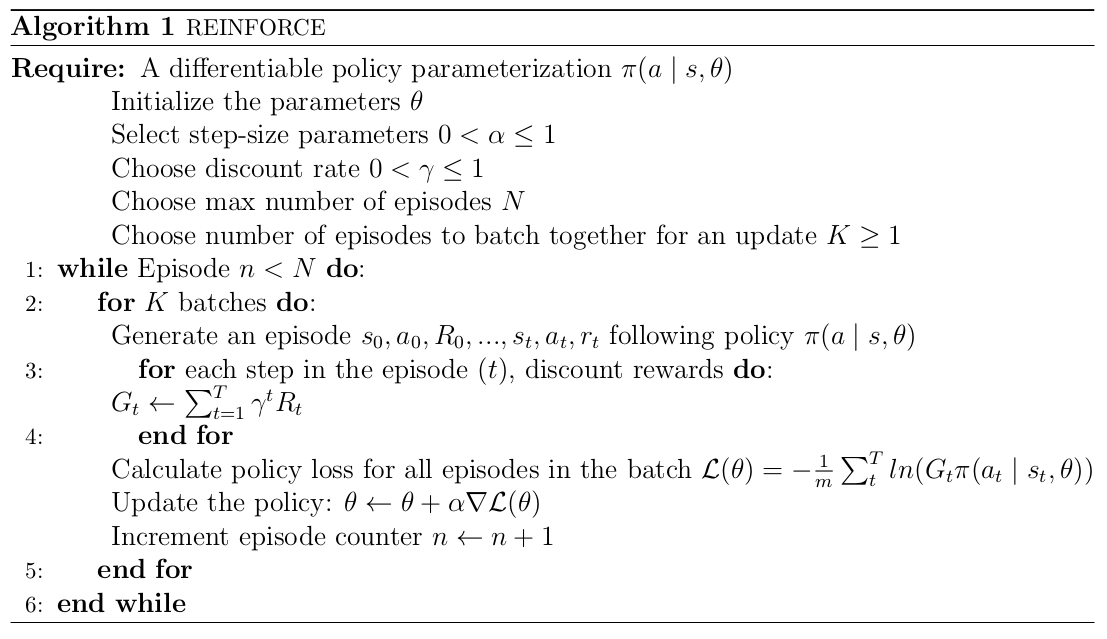
2. REINFORCE 알고리즘 프로세스

1. policy $\pi_{\theta_1}$을 Episode가 종료할 때까지 실행시켜 총 $T_1+1$개의 sample ($\mathbf{x_t, a_t}, r(\mathbf{x_t,a_t}), \mathbf{x}_{t+1})_{\ t=0,\ ...,\ T_1}$을 생성
2. 이를 바탕으로, $\pi_{\theta_1}$에서 $\pi_{\theta_2}$로 update 한다.
3. 그 후 $T_1+1$개의 sample은 바로 폐기
4. update된 policy $\pi_{\theta_2}$를 또 다른 episode가 종료할 때까지 실행시켜 다시 $T_2+1$개의 새로운 sample ($\mathbf{x_t, a_t}, r(\mathbf{x_t,a_t}), \mathbf{x}_{t+1})_{\ t=0,\ ...,\ T_2}$를 생성
5. 일정 학습 성과에 도달할 때까지 1~4 반복

---

3. REINFORCE 알고리즘의 문제점

1. 한 Episode가 끝나야 $\theta$(policy)를 update 가능
   • 이런 이유로 Monte Carlo Policy Gradient라고도 부름
   • 각 Episode가 상당히 긴 경우 신경망 학습 시간이 상당히 길어짐.
2. Gradient의 분산이 매우 큼
   • Gradient of objective function 값은 $G_t$ 값에 비례함
   • $G_t$는 Environment에 따라, 각 Episode의 길이에 따라 변화량이 상당이 큼.
     - 짧은 Episode는 긴 Episode에 비해 $G_t$ 값이 매우 작을 것
   • $G_t$가 Episode마다 크게 차이가 남에 따라 Gradient도 비례하여 값의 변동이 크며, 신경망 학습에 시간이 많이 걸리며 불안정, 학습이 안되는 결과 초래.
3. on-policy
   - policy를 update하기 위해서 해당 policy를 실행시켜 발생한 sample(Episode)이 필요하므로 효율성이 매우 떨어짐.

   on-policy, off-policy 차이점
   on-policy 학습은 agent가 현재 policy에 따라 행동하면서 학습하는 방법. agent는 현재 시점에서 수집한 데이터를 사용하여 policy update. 즉, policy의 성능을 평가하고 개선하기 위해 현재 policy를 사용하여 데이터 수집. ex. SARSA(s-a-r-s-a)와 A2C(Advantage Actor-Critic)

   off-policy 학습은 agent가 이전에 수집한 data를 사용하여 policy 학습하는 방법. agent는 과거에 수집한 data를 재사용하여 현재 policy를 평가하고 update. 이전의 policy를 통해 수집한 Experience를 이용하기 때문에 현재 policy와는 다른 policy 사용할 수 있음. ex. Q-leanring, DQN

On-policy의 장점
1. 안정적인 학습: 현재 정책에 따라 데이터를 수집하고 학습하기 때문에 학습 과정이 상대적으로 안정적
2. 수렴성 보장: 현재 정책을 평가하여 개선하기 때문에 수렴성(Convergence)을 보다 안정적으로 보장
3. 안전한 학습: 현재 정책을 기반으로 데이터를 수집하기 때문에 이전에 수집한 부실한 데이터로 인한 오류를 방지 가능