아이디어

• 약수를 에라토스테네스의 체 방식으로 더한다.
  • 주로 소수 판별에 쓰는 방법이다.
    
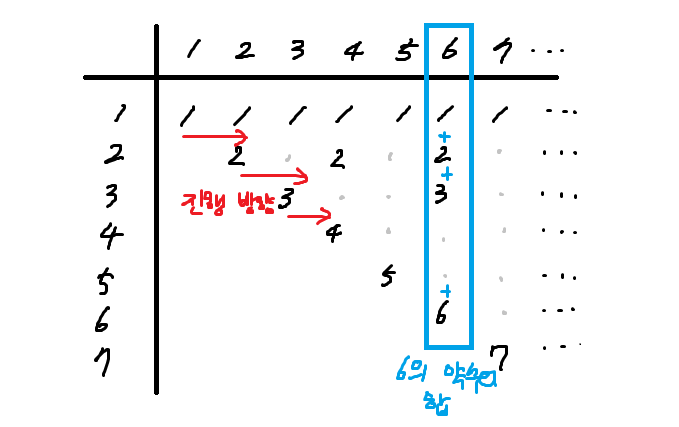
  • 1의 배수(자연수)는 모두 1을 약수로 가지므로 모두 1을 더한다.
  • 2의 배수는 모두 2를 약수로 가지므로 2의 배수번째에 모두 2를 더한다.
  • 3의 배수는 모두 3를 약수로 가지므로 3의 배수번째에 모두 3을 더한다.
  • … 이런식으로 2부터 $N$까지의 수에 대해 반복하면 약수의 합 $f(n)$을 구할 수 있다.
• $g(n)=\sum_{i=1}^n f(i)$는 누적 합 memoization을 이용해 구한다.

코드

import java.io.BufferedReader;
import java.io.InputStreamReader;

public class Main {
    static BufferedReader rd = new BufferedReader(new InputStreamReader(System.in));
    static StringBuilder sb = new StringBuilder();

    static int MAX = 1_000_000;

    static long f[] = new long[MAX + 1];
    static long g[] = new long[MAX + 1];

    public static void main(String[] args) throws Exception {

        for (int i=1; i<=MAX; i++) {
            for (int j=i; j<=MAX; j+=i) {
                f[j] += i;
            }
        }
        for (int i=1; i<=MAX; i++) {
            g[i] = g[i-1] + f[i];
        }

        int T = Integer.parseInt(rd.readLine());
        for (int t = 0; t < T; t++) {
            int n = Integer.parseInt(rd.readLine());

            sb.append(g[n]).append('\n');
        }
        System.out.println(sb);
    }
}

메모리 및 시간

• 메모리: 47836 KB
• 시간: 434 ms

리뷰

• 처음에 너무 어렵게 생각해서 못 풀 뻔했던 문제