알고리즘 문제풀이

결정하고자 하는 우리의 행은 이전 행이비어있다였으면 → 비어있다/왼쪽 칸에만 있다/오른쪽 칸에만 있다 3개 중 하나다.비어있다가 아니라면 → 비어있다/이전 칸과 다른 방향에 있다 2개 중 하나다.n번 행이 비어있다일 경우의 수를 $an$, 비어있다가 아닐 경우의 수를

주어진 그래프가 트리다. 트리는 사이클이 없으므로, 두 점을 잇는 경로가 항상 유일하게 된다. 따라서 이 문제는 외판원 문제가 아닌 단순한 탐색 문제다.문제에서도 그냥 ‘거리’라고만 명시되어 있다.인접 리스트를 나타내기 위해 Map\[] 변수를 만들었다.인접행렬로 나타

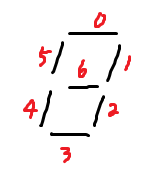
숫자의 7-segment 표현을 비트열로 옮길 것이다.각 (빨간 숫자)번 비트가 켜져 있으면 그 막대기가 켜져 있다고 한다.그 결과 길이가 최대 7인 비트열을 얻는다.이를 이용해 6자리 이하 임의의 십진수를 비트열로 나타낼 것이다.수의 각 자릿수에 대해 7-seg 비트

‘왼쪽 자식 < 부모 < 오른쪽 자식’임을 이용해 입력이 들어오면 루트부터 계속 비교하여 트리를 구성한다.부모보다 작을 경우 왼쪽으로 간다. 클 경우 오른쪽으로 간다. 같은 키를 가지는 경우는 주어지지 않는다.해당 자리가 비어있을 경우 자신이 자식이 된다.이

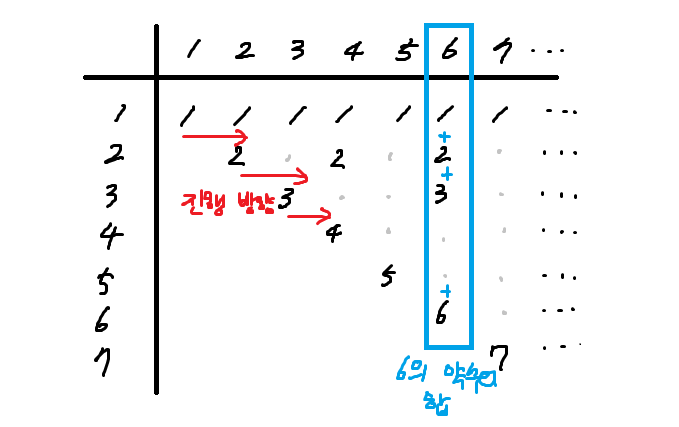
약수를 에라토스테네스의 체 방식으로 더한다.주로 소수 판별에 쓰는 방법이다.1의 배수(자연수)는 모두 1을 약수로 가지므로 모두 1을 더한다.2의 배수는 모두 2를 약수로 가지므로 2의 배수번째에 모두 2를 더한다.3의 배수는 모두 3를 약수로 가지므로 3의 배수번째에

육각수 $h_n$를 수식으로 구할 수 있다. 미리 필요한 $h_n$를 모두 구해놓았다.$n$일 때 육각형은 한 변이 $n$인 육각형이 추가되고(점 개수: $6(n-1)$) 이 중 $2n-3$개의 점이 겹친다.따라서 $hn = h{n-1} + 6(n-1) - (2n -

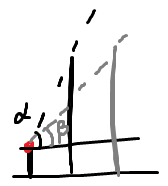
건물을 바라봤을 때의 각도가 앞의 건물을 바라봤을 때의 각도보다 작으면 그 건물은 보이지 않는다.위 그림에서 $\\beta < \\alpha$기 때문에 회색 건물은 보이지 않는다.각도가 (-)값이어도 마찬가지 (관찰자 쪽의 건물이 더 높을 때)에제 입력 3을 참고

만약 한 점부터 시작해서 연속해서 최대한 수열을 뽑으면, 최대 수열 길이와 같은 수의 시작점이 같은 연속된 수열을 얻는다.예를 들어 첫 번째 자리에서 시작해서 최대한 수열을 늘리면 1, 1, 2, 1, 2, 3 3개를 얻는다.마찬가지로 두 번째 자리에서 시작해서 최대

높은 자리에서 가장 많이 나오는 순서대로 9, 8, 7, …등을 할당한다.어떤 자릿수에 대해 나온 횟수가 동일하다면 다음으로 작은 자릿수를 비교하고, 우열이 결정될 때까지 반복한다.1의 자리에서도 결정이 안 난다면 그 둘 사이에는 어찌되도 상관 없다.각 문자가 등장할

2048 게임의 조작을 구현한다.위로 이동하는 경우를 생각해보자. 나머지도 방향만 다르게 하면 된다.우선 맨 위부터 빈 공간이 아닌 숫자가 있는지 탐색한다.숫자가 있으면 천장이나 다른 숫자에 닿을 때까지 위로 끌어 올린다.만약 끌어올린 후 위가 천장이 아니고, 위 숫자

입력을 받으며 0이 아닌 점 개수(cnt)를 세서 초기화한다.0이 아닌 아무 점을 찾는다.이때 점을 찾을 수 없었다면 빙산이 모두 물이 잠긴 상태고, 그 이전까지는 모두 연결되었다는 뜻이므로 0을 출력하고 종료한다.점을 찾았다면 그 점부터 그래프를 DFS로 탐색한다.B

문자열 패턴이 복잡하거나 없으면 Map을 쓰는 수밖에 없지만… 기왕 패턴이 주어졌으니 좌표를 정수로 매핑시켜 일반적인 그래프 탐색으로 만들기로 했다.(알파벳에 해당하는 수) \* 1000 + (숫자 좌표) 로 바꾼다.“A37” → 1037, “U238” → “21238

ㅈㄱㄴE가 V에 비해 크지 않으므로 Kruskal로 ㄱmake랑 union은 굳이 메소드 안 만들었습니다.나름 최적화한답시고 경로압축이랑 큰 번호쪽이 루트가 되도록?메모리: 49608 KB시간: 628 ms기본기는 확실히

n개 정점의 완전 그래프에 대한 MST간선의 가중치는 두 행성 간의 거리n이 작고 간선 수는 많으므로 PriorityQueue를 쓰지 않는 Prim 알고리즘을 사용해봄메모리: 14120 KB시간: 128 msn이 작을 때는 PQ를 안 쓰는게 더 빠를 수 있다.

N개의 행성을 모두 연결하는 Full graph로 풀 수 있을까?N ≤ 100,000, E = N(N-1)/2 이므로 어림도 없다.간선의 수를 줄여야 함백트래킹으로 유망성을 검사해서 미리 간선을 쳐낸다.메모리:시간:리뷰

다익스트라로 각 정점까지의 최단비용을 구해야 한다.시간복잡도: $n \\leq 10\\ 000$이므로 $O(n^2)$ 미만이어야 함우선순위 큐를 사용한 다익스트라 알고리즘(시간 복잡도: $O(n \\lg n)$)INF가 아닌 정점의 개수와 그 중 최댓값을 출력하면 끝메

경험치 보상이 작은 퀘스트부터 깨야 아케인 스톤에 최대한 많은 경험치를 누적시킬 수 있다.각 퀘스트를 깬 후 경험치와 이전까지 보유한 아케인 스톤 개수의 곱들의 누적합이 정답메모리: 57168 KB시간: 824 ms각 작업의 대기 시간의 합을 최소로 하는 방법은 처리

A1~Ai의 합을 Aacci라고 할 때, Aacc를 이진탐색하여 처음 Bi >= Aaccidx가 되는 idx를 찾으면 된다.Java의 Arrays.binarySearch()를 사용한다면, 탐색 실패 시 리턴되는 음수 값의 의미를 이용하면 빠르다. (https:

일단 예외처리: 모든 사람이 L만큼 먹어도 술이 부족(> T)하거나, R만큼 먹어도 술이 남으면(< T) S와 관계 없이 불가능한 경우이외의 경우에는 각자의 주량을 Li~Ri에서 잘 조절하면 정확히 합이 T가 되도록 할 수 있다.S는 L의 최댓값과 R의 최댓값 범

완전탐색 불가능그리디 불가능DP를 시도할 수 있나? 가능할 것 같다.'회의실 배정' 문제와 같이 종료 시각 순으로 정렬한 뒤, 가능한 모든 종료 시각에 대해 DP를 돌릴 수도 있겠다. 아래와 같은 형태가 되었을 것그러나 시각의 범위가 $2^{31}-1$까지므로 메모리

가격이 D 이상 차이나지 않도록 인접해야 한다는 점에서 투 포인터를 떠올려야 한다.선물을 가격순으로 정렬하고 투 포인터(Sliding window) 기법을 사용해야 한다.오른쪽 포인터를 옮기다 가격이 D 이상 차이나게 된다면 왼쪽 포인터를 한 칸 옮겨보는 작업을 반복하

문자열을 사전 순으로 정렬하면 어떤 단어의 접두사는 반드시 그 단어보다 위에 있게 된다.사전 순으로 정렬 후 역순으로 탐색하며 그 단어를 부분집합에 포함시킬 지 아닐지를 본다.현재 부분집합에 있는 어떤 단어에도 접두사가 되지 않으면 포함시키면 된다.메모리: 14244

아이디어 숫자 하나를 고정하고 나머지 둘을 선택해 합이 최소가 되는 것을 찾자. 케이스가 겹치지 않도록 고정하는 수는 가장 작은 수로 고정하자. 즉, 고정하는 수 i에 대해 i+1~N-1 범위만 탐색한다. 특성값 순으로 정렬해놓고, 범위의 시작과 끝에서 탐색을

구하고자 하는 '각 그룹의 합의 최솟값'을 이진탐색으로 구해보려 한다.범위는 0부터 어떤 큰 수까지 시작한다.이진 탐색의 mid 값을 최솟값으로 해서 만들 수 있는 그룹의 수를 구한다.만약 그룹의 수가 K보다 많다면, 더 큰 최솟값을 가지도록 나눌 수 있었다는 뜻이므로

위상정렬 알고리즘을 사용한다. 단, 현재까지의 건설 시간이 짧은 순으로 탐색해야 하므로 PQ를 사용한다.위상 정렬 알고리즘:각 노드의 진입 차수를 기록해 놓는다 (indeg)진입차수가 0인 노드를 큐에 넣고 시작한다.여기서는 현재까지의 건설 시간 정보도 함께 PQ에 넣

문제가 최적 부분문제의 형태를 가진다.구하고자 하는 것은 1~K번을 모두 합치는 '최소 비용'이다. \* i~j번을 모두 합쳤을 때의 최소 비용을 costi라 하자.한편, 그렇게 합쳤을 때의 파일 크기를 sizei라 하면, i ≤ k < j에 대해이 되고, 그때

문제는 부분 최적 구조를 가진다. 필요한 변수를 고려해보자.y, x: 좌표 - (1, 1)부터 (y, x)까지 오는 경우의 수를 세어야 한다.c: (y, x)까지 거쳐온 오락실 수 - (y, x)까지 오기 까지 거쳐온 오락실 수가 모두 다를 수 있다.m: (y, x)

이웃은 4방 탐색이웃이 검은 방이면 깊이가 1 증가한다.PQ를 사용한 다익스트라메모리: 14516 KB시간: 136 ms이것도 일단은 다익스트라긴 하네

문제가 중복 부분문제 구조를 가진다. DP를 적용해보자.1 ~ i 구간 중에서 길이 L의 기관차 k개 놓았을 때 최대 부분합 f(k, i)은, i번에서 끝나도록 L개를 연속해서 선택하는 경우와 아닌 경우로 나뉜다.첫 번째 경우는 1 ~ i-L 구간에서 k-1개를 놓고,

1개의 다리는 가중치가 T인 S→E 간선과 E→S 간선으로 취급한다.1개의 웜홀은 가중치가 -T인 S→E 간선으로 취급한다.그래프가 음의 간선을 포함하므로 벨만-포드 알고리즘을 사용해야 한다.벨만-포드 알고리즘: 모든 간선을 V-1번 탐색하며 최솟값으로 거리를 갱신한다

"최소 개수의 회선만을 복구, 모든 노드 연결" -> 이미 연결된 노드를 다시 연결하지 않는다."다른 컴퓨터와의 통신에 필요한 시간 평균 최소" -> 모든 노드의 최단거리(시간) 합이 최소자신과의 거리는 0이므로 자신을 포함시켜도 상관 없다.모든 두 점 간의 최단거리를

기본 베이스는 BFS로 탐색한다.BFS의 파라미터로 벽을 부술 수 있는 횟수를 같이 기록해야 한다.그러니깐 방문 체크 배열은 벽을 부술 수 있는 횟수를 나타낼 변수를 추가해 3차원으로 나타내자.만약 도착한 칸이 벽이고, 벽을 부술 수 있는 횟수가 남아있으면 횟수를 1

위상정렬 알고리즘을 사용한다. 자세한 설명은 여기 참고단, 진입차수가 0이라도 그 중에서 번호가 작은 것을 골라야 하므로 일반 큐 대신 우선순위 큐를 사용한다.메모리: 44772 KB시간: 516 ms1005번보다 더 쉽고 직관적인데 왜 골드2인지 의아한 문제

위상정렬 알고리즘을 사용한다. 자세한 설명은 여기 참고간선 연결을 끊을 때마다, 끝 정점보다 시작 정점의 Strahler 순서가 더 크면 끝 정점의 순서를 그걸로 갱신한다.간선 연결을 끊을 때마다, 끝 정점과 시작 정점의 Strahler 순서와 같으면 이전에 적어도 한

모든 컴퓨터를 연결하는 데 최소 비용이 들도록 한다. → 최소 스패닝 트리 문제Prim 알고리즘의 시간복잡도는 $O(V^2)$ 또는 $O((V+E)\\lg V)$로, 우선순위 큐를 사용하면 풀이가 가능하다.Kruskal 알고리즘의 시간복잡도는 $O(E \\lg E)$로

백준 11053 '가장 긴 증가하는 부분 수열'에서 사용할 수 있는 알고리즘, $i$에 대해 $1\\le j < i$ 중 $A_j < A_i$인 것들의 최대 memo\[j] 값을 선형 탐색하는 방법은 $O(N^2)$의 시간복잡도를 갖는다.그러나 이 문제에서는

문제의 2번, 3번 특징에서 MST 문제임을 알 수 있다.문제의 1번에서, 남초-남초 간선과 여초-여초 간선은 제외해야함을 알 수 있다.MST를 구하기 위해 Kruskal 알고리즘을 사용했다.$N \\le 1\\ 000$이므로 Prim을 써도 상관 없을 것이다.간선 개

$t$: 테스트 케이스 수길이 $n$인 배열 $a$에 대해 $f(l, r) = al \\ \\&\\ a{l+1}\\ \\&\\ \\dots \\ \\&\\ a_r$이라 하자.$1 \\le l \\le r \\le n$, $\\&$는 bitwise AND주어진 $n$

BFS를 사용한다.단, 이전에 탐색한 칸이라도 획득한 열쇠들이 다르면 재탐색해야 한다.열쇠가 있다면 문을 열 수 있기 때문이다.따라서 방문 여부 체크 배열(여기서는 enqueued)는 열쇠 상태과 좌표를 포함한 3차원 boolean 배열이 된다.여기서 열쇠 상태를 비트

문제가 어렵게 쓰여있는데, 결국 i에서 j로 가는 경로의 길이를 Di라 하면 모든 j에 대한 Di의 합 중 최솟값을 구하라는 문제이다.BFS를 써도 되고, 모든 가중치가 1인 그래프로 생각해 Floyd-Warshall 알고리즘을 써도 된다.당연히 BFS 쪽이 더 시간복

주어진 정보는 정점이 $N+2$개이고, 맥주병 20개(1000 미터)안에 갈 수 있는 정점끼리 연결된 그래프라고 생각한다.0번 정점은 상근이네 집, 1~$N$번 정점은 편의점, $N+1$번 정점은 펜타포트 락 페스티벌을 나타낸다. 해당 그래프에 대해 DFS나 BFS를

각 칸이 물에 잠기기까지 남은 시간을 구한다.초기에는 물이 있는 칸에는 0, 돌과 비버굴은 -1, -2로 따로 표시해서 예외처리를 하고, 나머지 칸은 $\\infty$로 둔다.물 칸에서 BFS를 이용해 물에 잠기기까지 남은 시간을 갱신한다.고슴도치의 위치에서 BFS로

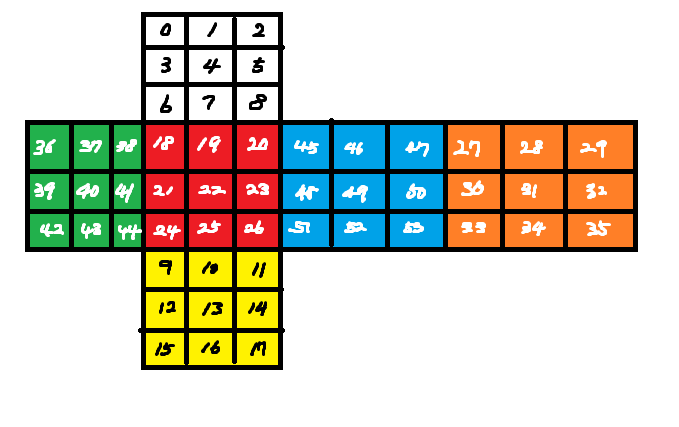
모든 54개 면에 대해 위 그림처럼 인덱스를 붙이자.모든 12개 회전에 대해 대응되는 인덱스 쌍의 집합을 하드코딩한다.입력을 회전 인덱스로 바꾸어 회전을 수행한다.인덱스 0~8번이 윗면을 나타내므로, 이 부분을 출력한다.메모리: 19804 KB시간: 208 ms아마 이

아이디어 KMP 알고리즘의 튜토리얼 격 문제 패턴 매칭 중 불일치가 발견되면 다음 탐색은 처음부터가 아닌 해당 불일치가 발견되기 전까지의 서브패턴 중 반복되는 패턴 부분으로 돌아가는 방법 이를 위해 pi[]라는 배열을 만든다. pi[i]: P[0..i] 서

맵 전체를 탐색하며 섬을 발견하면 사방 탐색으로 인접한 모든 섬 타일에 번호를 붙인다.DFS, BFS 중 DFS를 사용하였다.이 섬 번호는 그래프에서 정점 번호로 사용한다.맵 전체를 탐색하며 섬 타일이라면 4방향으로 다리를 뻗어본다.다리가 같은 섬에 이어진다면 취소한다

주어진 16진수를 4개로 끊어 정수 형태로 배열에 저장한다.회전해야하는 최소 횟수는 $N/4 - 1$번이다. 회전은 각 끝자리를 떼어 저장한 후, 16진법에서 오른쪽 밀기와 같은 효과를 가지도록 각 수를 16으로 나눈다. 이후 떼어놨던 끝자리를 오른쪽 숫자의 가장 큰

격자에서의 다익스트라$O(E \\lg V)$의 우선순위 큐 다익스트라 알고리즘을 사용하였다.정점 번호가 2차원으로 나타난다. dist 배열(시작점에서 해당 정점까지의 최단거리)도 2차원이 된다.인접한 정점 번호는 4방향에 인접한 좌표와 같다.시작 정점으로부터 자신까지의

맵 데이터의 원본을 따로 저장해놓는다.구슬을 N번 명중시킬 N개의 x좌표 쌍의 경우의 수를 모두 탐색한다. (중복순열)순열을 얻었으면, 해당 쌍을 가지고 시뮬레이션을 시작한다.당연히도 시작 전 맵을 원본 상태로 초기화시켜야 한다.시뮬레이션 과정은 아래의 과정을 N번 반

풀이가 떠오르지 않을 때는 완전탐색부터 고려해보자.$K$를 $\\max(A)$부터 $\\sum A$까지 모두 탐색하면 조건을 만족하는 $K$의 최솟값을 찾을 수 있지만, 시간복잡도가 $O(N \\times \\sum A)$이 되서 시간 내 풀이가 어렵다. ($\\sum

다익스트라로 최단경로를 구하는 메소드를 만든다.그래프는 인접 간선을 빠르게 찾기 위해 인접리스트로 나타냈다.Priority queue를 사용하는 다익스트라를 사용하였다.시간복잡도 $O(M \\lg N)$(i..X 최단경로 길이 + X..i 최단경로 길이) 중 최댓값을

$1..v_1$, $v_1..v_2$, $v_2..N$, $1..v_2$, $v_1..N$ 경로 최단거리를 구한다. (L1~L5라 하자.)인접행렬 그래프에서의 다익스트라를 이용했다.시간복잡도 $O(N^2)$$1..v_1..v_2..N$ 경로 길이 L1+L2+L3와 $1

100 단위마다 끊어서 필요 동전 수를 세자.1~100까지의 최소 동전 수는 DP로 구할 수 있다.$f(i) = \\min{(i-1), f(i-10), f(i-25)} + 1$ ($i < 0$이면 무시)메모리: 65832 KB시간: 516 ms그리디 단골로 나오는

게임 이론: 모든 플레이어가 최선의 선택을 함을 가정한다.부분문자열을 만들수 없을 때, 즉 게임판에 0~9의 수가 적혀있으면 패배한다.i의 진부분문자열 ps에 대해i - ps가 패배한다면 i는 플레이어 1이 승리하는 수다.i - ps가 승리한다면 다음 턴에서 플레이어

작업 중 변경된 내용이 반영된 값을 참조하지 않도록 원본 배열 A를 복사한 tmp 배열을 만들자.1초에서의 모든 작업이 끝날 때 마다 tmp의 변경사항을 A에 반영(commit)한다.공기청정기의 경우, 순환 경로를 미리 구성해놓자.메모리: 14908 KB시간: 272

구하고자 하는 답인 H\_{MaxHp}에 대해 매개변수 이진탐색 한다.초기 left = 1, right = 123000 \* 100만 \* 100만 + 1이다.최악의 경우 공격력이 100만인 적을 공격력 1로 싸울 때 100만 대를 버텨야하므로설정한 최대체력으로 게임을

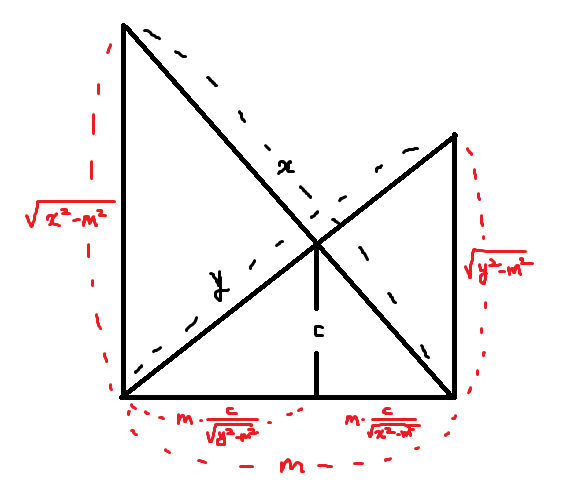
위 그림에서 $a = \\sqrt{x^2-m^2}$, $b = \\sqrt{y^2-m^2}$라 하면$m\\frac{c}{a} + m\\frac{c}{b} = m$$\\frac{1}{a} + \\frac{1}{b} = \\frac{1}{c}$$c = \\frac{1}{\

L과 R 모두 같은 자리에 '8'이 있으면 L~R 사이에 있는 수의 해당 자리는 무조건 '8'이어야 한다.단, 그 이전 자리에 '8'이 아닌 다른 숫자가 있었다면 8이 없어도 된다.메모리: 14292 KB시간: 124 ms두번째 조건을 잘 생각해봐야 하는 문제.예제 입

부분 최적문제이므로 dp로 풀어보자.memo\[날짜]\[지각횟수]\[결석횟수]와 같이 3차원 동적 테이블을 정의하자.각 날짜를 1일자부터 돌며 현재 날짜가 출석, 결석, 지각일 경우를 처리한다.출석일 때: 지각 횟수는 그대로, 결석 횟수는 0이 된다.결석일 때: 지각

같은 파티에 참여한 사람들은 같은 집합으로 묶는다.최초로 진실을 아는 사람은 집합 0에 있다고 하자.예를 들어 진실을 아는 사람과 같은 파티에 있던 모든 사람은 집합 0(진실을 앎)에 속하게 된다.진실을 알고 있을 때 항상 대표자가 집합 0이 되도록 union 함수는

갔다가 1번 장소로 돌아오는 시간을 제외하고, 남는 시간 동안 가능한 행복도 합이 높은 두 장소를 왔다갔다 하는 것이 좋다.$i$번째 장소에서 $i+1$번째 장소로 이동했다면 $i+1$번째 장소에서 $i$번째 장소로 되돌아가야 한다.따라서 이때 얻는 행복도는 반드시 $

석순에 대해서 먼저 생각해보자.높이가 $i$인(즉 $i$번째 구간까지 뻗어있는) 석순의 개수를 d\[i]라 하면 개똥벌레가 $i$번째 구간으로 날고 있을 때 부숴야 하는 석순 개수는 d\[N] + d\[N-1] + ... + d\[i]다.마찬가지로 $i$번째 구간까지

DFS로 트리의 높이(DFS의 최대 깊이)를 탐색한다.dfs() 메소드의 리턴값을 이용해 높이를 측정한다.현재 노드에서의 트리의 높이(DFS의 최대 깊이)가 $D$보다 크다면 해당 경로로 갔다 돌아와야 하므로 답에 +2를 더한다.메모리: 70236 KB시간: 568 m

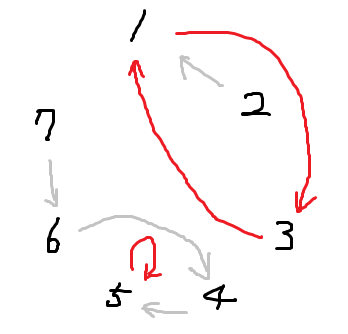
(예제 입력 1에 대한 그래프)집합 내의 원소는 순서 상관 없이 모든 원소가 중복되지 않고 포함되어야 하므로 항상 집합 크기와 같은 길이의 사이클이 생긴다.재귀적으로 표를 참조하며 경로를 이으면 위와 같이 규칙을 볼 수 있다.참조를 타고 자기 자신으로 돌아올 수 있으면

숫자를 고르는 최소 횟수를 DP로 구한다.숫자 i를 만드는 데 필요한 수의 개수 = 숫자 (i-마지막으로 사용한 정수)를 만드는 데 필요한 수의 개수 + 1\[마지막으로 사용한 정수]구하는 중 횟수가 K를 넘어가면 해당 숫자에서 승자가 결정된다. 숫자의 홀짝 여부로 승

index 0부터 순서대로, 자신보다 뒤에 있는 원소 중 남은 횟수의 swap으로 끌어올 수 있는 최대 원소를 선택해 자기 자신으로 끌어오면 된다.메모리: 14288 KB시간: 128 msLinkedList를 사용하면 시간복잡도를 개선할 수 있을 것 같다.채점이 느릿느

정답은 숫자의 길이, 현재 등장한 숫자들의 집합, 그리고 마지막으로 자리에 영향을 받는다.이전 길이와 이전 길이의 숫자 집합, 마지막 자리에 따라 부분문제 관계가 성립한다.$f(i, S, j) = f(i-1, S - {j}, j) + f(i-1, S, j)$구하는 답은

구하는 값은 이전까지 구했던 힘의 합에 새로 밟는 움직임에 대한 힘을 더하는 형태로 이루어진다.즉, 부분 중복문제, 최적 부분문제의 형태를 띄고 있다.DP를 생각하여, 필요한 변수를 생각해보면, 현재 길이, 왼발과 오른발의 위치에 영향을 받음을 알 수 있다. 따라서 3

그래프는 인접행렬로 받는다.모든 도시에 대해 연결된 도시끼리 분리집합(union-find)를 형성하자.여행 계획에서, 인접한 두 점끼리 같은 집합에 있으면 해당 두 도시 사이에는 경로가 있다는 뜻이다.중간에 경로가 끊기는 도시가 있다면 "NO", 아니면 "YES"다.메

최단경로 찾는 문제니 Dijkstra로 푼다.$O(V^2)$이어도 상관 없다.경로 찾는 방법어떤 점에 도달하는 최단경로는, 그 점의 이전 점까지 도달하기 위한 최단경로를 반드시 지난다.Dijkstra는 시점부터 종점까지 거치는 모든 경로상 점에 대해 최단거리를 구할 수

변수가 4개 있다. (현재 레벨 $n$, 빨강 $r$, 초록 $g$, 파랑 $b$)4차원 동적 테이블을 사용한다. 여기서는 $f(n, r, g, b)$라 쓰자.경우를 나눠보자.$n$이 1로 나누어 떨어지는 경우(모든 경우): 빨강, 초록, 파랑을 사용하는 3가지 경우를

각 질문에 대해, 중앙값을 기준으로 길이를 늘리다 비대칭이 되는 지점이 있으면 그 이후부터는 모두 비대칭이다.모든 가능한 S, E 조합에 대해 위와 같은 논리를 적용해 답을 구한다.길이가 홀짝인 경우로 구분하는 것이 좋다.메모리: 218628 KB시간: 892 ms루프

오른쪽으로 범위를 늘리다가, 부분합이 $S$ 이상이 되면 왼쪽 끝에서부터 부분합에서 반대로 빼보며 길이를 얼마나 낮출 수 있는 지 본다.만약 부분합이 전체 합이라도 $S$ 이상이 되지 못하면 "0"을 출력한다.메모리: 23820 KB시간: 284 ms투 포인터 문제도

기본적으로 브루트포스백트래킹을 이용해 가망이 없는 스도쿠 상태로 접근할 수 없도록 해야 한다.스도쿠의 게임 규칙을 위반하게 되는 상태가 되면 이전 상태로 되돌아간다.가로줄, 세로줄, 또는 해당 칸이 위치한 3x3 블록 내에 같은 숫자가 없어야 한다.이러한 조건은 비트마

MST는 $N-1$개의 간선을 가져야 한다.만약 여기서 하나의 간선이 끊어질 경우, 그래프가 두 개의 연결그래프로 나뉜다.따라서 기존 MST와 달리 $N-2$개의 간선을 짧은 순서대로 연결한다.Kruskal을 사용하자.메모리: 332564 KB시간: 1732 ms메모리

각 점을 분리집합으로 관리하자.분리집합을 합집합(union)할 때 서로 같은 집합에 합집합을 하게 된다면 사이클이 생기는 경우다.메모리: 150212 KB시간: 536 msUnion-find 코드를 더 효율적인 것으로 외워놔야겠다.

토네이도 표현토네이도의 바람은 방향과 세기로 나눌 수 있다. \* 방향은 ←, ↓, →, ↑ 순서로 계속 회전한다.세기는 1, 1, 2, 2, 3, 3, ..., N-2, N-2, N-1, N-1, N-1과 같이 세기가 증가하며 2번씩 등장한 후, 추가로 N-1 세기

Doubly linked list 형태로 변경 내역(hist ← history)를 관리하자. 현재 가리키고 있는 노드를 head라 하자.최초의 head는 -1 값을 가지고 있는 더미 노드다.hist\[i]에는 i번째 변경 전의 head를 가리킨다.'추가' 쿼리라면 새

크게 상어 잡기, 상어 이동, 잡아먹기로 나뉜다.해당 열의 상어를 빠르게 탐색하기 위해서는 2차원 지도 기반의 자료구조(map)가 필요하다.한편, 상어 전체를 관리하는 자료구조(sharks)가 필요하니 둘 다 사용해야 한다.상어 이동2(R-1) 또는 2(C-1) 칸 이

핵심 아이디어는 숫자를 지웠을 때 왼쪽이 가장 크도록 하는 것이다..입력은 Doubly linked list를 사용해 받았다.수의 가장 첫 자리부터 탐색한다.만약 지울 수 있는 횟수 k가 남아있고, 다음 자리보다 더 작은 숫자라면 지운다.아니라면 다음 자리로 이동한다.

아이디어 4가지 연산을 수행하는 경우를 그래프가 이어진 것으로 생각하여 풀어야 하는 문제 가장 연산 수가 짧은 것을 찾아야 하므로 BFS으로 찾아야 한다. 코드 메모리 및 시간 메모리: 24644 KB 시간: 840 ms 리뷰 이 문제를 stack을 이용해 풀 수

사이클을 감지해야한다는 점에서 위상정렬을 시도해봤다.메모리: 305408 KB시간: 1104 ms풀긴 풀었는데, 메모리와 시간을 봐서 정해는 아닌 것 같다. 더 효율적인 풀이를 찾아봐야겠다.

관계를 그래프(인접리스트)로 가지고 N번 부품(완제품)부터 해체해보자.이때, 다른 상위 제품이 남아있을 때 해체를 해버리면 상위 제품을 해체할 때 다시 재해체해야하므로, 상위 제품이 남아있지 않은 부품만 해체하자.이는 그래프의 입력차수가 0인지 아닌지를 보면 된다. 즉

고객 p\[j]명을 늘리기 위해 co\[j]의 비용이 든다고 하면...고객을 i명 늘이기 위한 최소 비용 memo\[i]는 memo\[i - p\[j]] + co\[j]의 최솟값이다.고객을 '최소' C명 이상 늘리면 되므로 memo\[C]~memo\[C + (p\[i]

기본적으로 $1, 2, ..., a-1, \\max(a, b), b-1, b-2, ..., 2, 1$ 순서를 유지하면 가희와 단비가 볼 수 있는 건물의 수에 대한 조건을 만족할 수 있다.남은 빈 자리에는 높이 1의 건물을 가능한 왼쪽부터 채우면 될 것이다.이때 $a =

모든 칸 (y, x)에 대해, 단어의 글자 수 Z에 대해 인덱스 Z-2에서 역순으로 현재 위치와 갈 수 있는 위치의 글자가 단어의 i번과 i+1번이라면 memoix에 memo\[i+1]\[new_y]\[new_x]만큼 경우의 수를 더한다.모든 칸에 대해 memo\[0]

다음 행렬식을 사용한다.$\\begin{bmatrix} F{n+1} & F{n} \\ F{n} & F{n-1} \\end{bmatrix}=\\begin{bmatrix} 1 & 1 \\ 1 & 0 \\end{bmatrix}^n$거듭제곱은 분할 정복 방식으로 구현한다.합

문제를 잘 읽고 문제에서 제시된 모듈로 연산, 모듈로 역원과 페르마의 소정리를 잘 구현하면 되는 문제$X=1\\ 000\\ 000\\ 007$일 때 $S_1N_1^{X-2} + S_2N_2^{X-2} + ... + S_MN_M^{X-2} \\pmod{X}$를 계산하면

조합과 그래프 탐색칸마다 벽을 세우는 경우와 안 세우는 경우를 모두 탐색한다.벽을 3개 세웠다면 시뮬레이션 한 후 빈 칸의 개수를 구해 답을 갱신한다.시뮬레이션은 BFS, DFS 어떤 방법으로도 상관 없다.구현이 간단하도록 모든 칸에 대해 DFS를 돌리는 방식으로 구현

각 칸의 꼭짓점을 정점으로 하고, 타일의 선으로 연결되어 있으면 가중치가 0이고 반대 방향으로 놓아져있으면 1인 그래프를 생각하자.이 그래프의 크기는 (N+1)x(M+1)이다.이때 0-1 BFS를 이용해 (0, 0)부터 (N, M)까지 가는 최단거리를 구한다.이때, e

단순히 입력 처리가 번거로운 순열 문제처럼 보이지만 핵심은 입력받은 수의 중복도만큼만 중복될 수 있다는 것에 있다.각 수의 등장 횟수는 배열 B에 기록했다.1번 이상 등장한 수만 모아 배열 A에 저장해두자.A에 대해 중복순열을 작성한다. 이때, 숫자가 등장했다면 사용할

기본적으로 BFS문인 경우, 열쇠가 있으면 큐에 넣고 없으면 임시 리스트에 넣는다.열쇠를 얻으면 임시 리스트에 있는 위치를 모두 큐로 옮긴다.메모리: 22528 KB시간: 204 ms귀찮은 구현 문제예전에 백준 1194 '달이 차오른다, 가자'와 비슷하다고 생각해서 비

백준 1697 '숨바꼭질'와 같은 원리의 BFS메모리: 34712 KB시간: 208 msint d를 이상한 데에다 놓는 실수를 해서...

거짓말 한 사람이 $k$명일 때를 생각해보자.이때, "거짓말한 사람이 "$0$명 이하", "$1$명 이하", "$2$명 이하", ..., "$k-1$명 이하"라 한 사람들과 "$k+1$명 이상", "$k+2$명 이상", ..., "$N$명 이상"이라고 한 사람이 거짓말

"비용"이 weight(cost), "메모리"가 value가 되는 가방 문제2차원 배열 memo\[i]\[j]를 사용한다.memo\[i]\[j]: 앱 $A_1$~$A_i$을 고려했을 때 비용 합이 j\`인 경우 메모리 합memo\[N]\[i]가 M일 때 i의 최솟값을

구현 문제타겟을 찾는 건 BFS로 구현하자.규칙을 적용하기 위해 PriorityQueue를 적용했다.BFS 데이터에 depth를 넣어 PQ 비교함수에 적용하거나, depth를 세기 위한 Queue와 PQ를 동시에 사용하는 방법필자는 후자를 사용했다.메모리: 14684

기본적으로 순열을 이용한 문제메모리 제한이 널널하다는 점에서 공간복잡도가 큰 방법이 가능함을 의심해볼 수 있다.만들어진 문자열을 HashSet에 저장해서 중복되는 문자열일 경우 제거한다.이것이 가능하다고 판단하기 위해서는 HashSet에 대해 이해해야 한다.해시 함수를

기본적으로 입력을 오름차순 정렬 후 순열을 이용한 브루트포스 문제문제에서 주어진 수는 모든 다른 수라고 보장하였으므로, 중복된 수열이 나오는 일은 절대 없다. 따라서 이에 대해 처리하지 않아도 된다.메모리: 123196 KB시간: 616 ms이전에 푼 'N과 M (12

$n \\le 100$ 정도이므로 Floyd-Warshall을 떠올려 볼 수 있다.Floyd-Warshall을 사용해 그래프의 모든 두 정점간 최단 거리를 구하자.각 $v_1$에 대하여 $v_1 \\rightarrow v_2$ 최단 경로가 $m$ 이하인 $v_2$의 합

기본 LCS 코드에 출력할 문자를 가지는 linked list를 추가한다.LCS DP는 코드 참고메모리: 46012 KB시간: 172 ms백준 9019 'DSLR' (리팩토링)에 이어 어떤 문자열의 길이를 구하는 방법을 문자열 자체로 구하는 문제로 치환할 수 있을 것

문자열을 한 글자씩 넣는다. 넣을 때마다 stack 맨 윗부분의 l 글자가 폭발 문자열인지 본다. (l은 폭발 문자열의 길이)시간복잡도: $O(nl)$ (n은 문자열의 길이)36×100만 정도이므로 가능주의: StringBuffer에 출력 결과를 저장할 때 sb.ins

먼저 가능성에 대해 알아보자.가장 naive한 반복: 시간 $O(Qn)$ → NO모든 $f_n(x)$ 메모이제이션: 시간 $O(Q)$ → OK, 공간 $O(mn)$ → NO그렇다면 중간은 없나?2의 제곱수에 대해서만 $f_n(x)$를 저장해두자.찾아올 때는 $n=(\\

BFS나 DFS를 사용하여 탐색하면 될 것 같다. 여기선 BFS를 사용해보겠다.이때, 도착한 점이 같더라도 이전에 갔던 경로가 다르면 다른 경우로 취급해야 한다.따라서 방문 배열을 전역적으로 사용하는 게 아닌, 각 도착점마다 가지고 있어야 한다.다행히 $1 \\le R

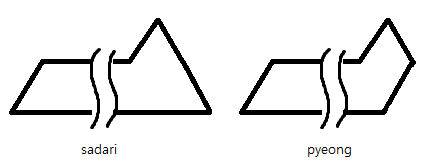
1층이 밑면이 길이 $n$인 사다리꼴, 평행사변형이 되는 경우의 수를 sadari\[n], pyeong\[n]이라 하자.이때, sadari\[i]는 다음과 같이 2가지 경우가 있다.pyeong\[i]의 오른쪽에 삼각형을 추가sadari\[i-1]의 오른쪽에 평행사변형(

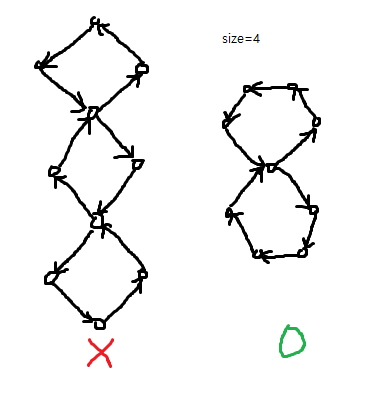
각 그래프 별 특징적인 정점을 찾으면 된다.추가된 정점 $A$: 입력차수 = 0, 출력차수 ≥ 2막대그래프다른 두 정점과 달리 경로를 따라갔을 때 끝나는 정점이 있다.끝 정점: 출력차수 = 08자 그래프8자 모양의 교차점이 있다.교차점: 입력차수 ≥ 2, 출력차수 2도

경로 내에 행성이 중복되도 상관 없다고 하였으므로, 우선 두 행성 간의 최단거리를 모두 구하자.$n \\le 10$이므로 시간복잡도 $O(n^3)$인 Floyd-Warshall 알고리즘을 사용해도 된다.이후, $K$부터 시작하여, 가능한 모든 경로를 탐색하자.시간복잡도

memo\[i]\[j]를 "$0$~$i$번째 파이프까지 봤을 때 파이프 총 길이가 $j$가 되는 경우의 수"로 정의하자.관찰이전 차례($i$-루프)의 memo값은 유지된다.추가로 $k$=$1$~$C_i$에 대해 이전 차례에서 총 길이가 $j-L_ik$가 되는 경우의 수

아이디어 문제에 나온 "GCD(n, k) = 1을 만족하는 자연수 1 ≤ k ≤ n 의 개수"를 오일러 피(phi) 함수 $\varphi(n)$이라 한다. 이에 대한 설명은 나무위키 등에 자세하게 나와 있지만, 주요한 성질을 정리해보고 가자. i) 소수 $p$에 대

이 풀이는 직전 포스트인 "백준 7569 '토마토'"의 풀이에 이어 수정된 코드를 기준으로 서술하겠다. 같이 참고하면 좋다.또한 7576번 (2차원 토마토), 7569번 (3차원 토마토)과 완전히 같은 논리로 11차원 배열과 11중 for문을 사용해서 문제를 풀 수도

dfs(y, x)가 좌표 (0, 0)~(y, x)에 대한 경로의 경우의 수를 구하는 함수라 하자.이때 dfs(y, x)는 4방향의 주변 칸 중 내리막으로 내려오는 칸 (y+dy\[d], x+dx\[d])에 대한 dfs 값의 합이다.계산이 중복될 수 있는 부분은 memo

문제에 나온 "GCD(n, k) = 1을 만족하는 자연수 1 ≤ k ≤ n 의 개수"를 오일러 피(phi) 함수 $\\varphi(n)$이라 한다. 이에 대한 설명은 나무위키 등에 자세하게 나와 있지만, 주요한 성질을 정리해보고 가자.i) 소수 $p$에 대해 $\\va