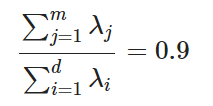Concept

• reduce the number of variables of a data set while preserving as much information as possible
• a dimensionality-reduction method which transforms a large set of variables into a smaller one that still contains most of the information in the large set
• this comes at the expense of accuracy but the trick is to trade a little accuracy for simplicity

Process

compute the covariance matrix

• What is Covariance Matrix?
  • p x p symmetric matrix that has the covariances associated with all possible pairs of initial variables
    
• How do you compute it?
  
  

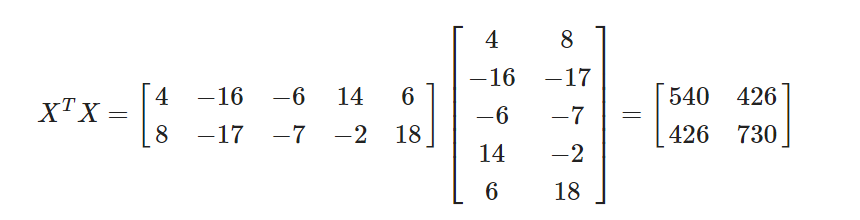
Compute the eigen vector and eigen value of the covariance matrix

• Definition of eigen vectors
  
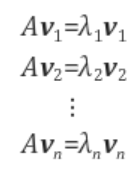
• Determinant of (A-λE)has to be zero because otherwise, eigen vector will be zero
  
  

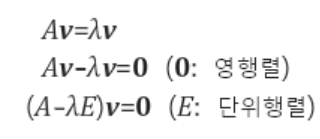
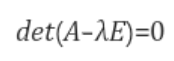
  Eigen Value is the variance of the model ( how much of the variables can be explained)

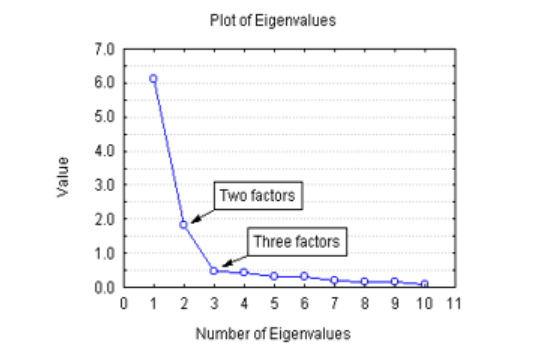
How Many Dimensions are we going to use?

1. Set a target variance

• e.g. 90% → sum of eigen value should be equal to this amount
  

2. Use the elbow method

• 

Why do we use eigen vectors and eigen values of the covariance matrix?

ref. 공돌이의 수학 노트 - 주성분 분석(PCA)