🔪소개및 개요

💎개요

안녕하세요~!!
저번에는 기본적인 경사하강법(MSE)를 사용하여 1차원의 x값만이 들어가는 선형회귀를 구현해봤습니다.

이번에는 로지스틱회귀와 행렬곱셈을 이용한 다중입력도 구현해보겠습니다.

💎환경

통합개발환경: DevCpp
언어: C++17
운영체제: Windows11 Home
컴파일러: g++

🔪로지스틱회귀

💎시그모이드 함수

우선 로지스틱회귀하면 빠뜨리면 안되는 함수 "sigmoid function"에 관하여 설명드립니다.

로지스틱회귀 특성상 된다또는 안된다라는 경우밖에없다보니, 방정식에 나오는 임의의 수가 0또는 1일 확률은 매우적습니다.
여기서 시그모이드함수는 0보다 작거나 1보다 큰 실수들을 0~1사이값으로 바꾸기위해 고안된 방법입니다.

우선 시그모이드 함수는 이렇게 생겼습니다.
$f(z) = \frac{1}{1+e^{-z}}$

보시다시피 아무리 수가 작던 크던 모두 0과 1에 근접한 값에 수렴하는것을 보실수 있습니다.

이제 이 함수를 실제 C++코드로 옮겨보겠습니다.

#include <cmath>

// 첫번째 방법
double sigmoid_1(double z){
	return (1 / (1 + std::exp(-z)));
}

// 두번째 방법
double sigmoid_2(double z){
	return (1 / (1 + std::pow(std::numbers::e, -z)));
}

두 코드는 메모리관점에서 보자면 미세하게 다르지만,
계산된 결과와 수학적관점에서 바라보면 완전히 일치합니다.

함수 sigmoid_1은 자연상수e에 첫번째인자만큼 제곱을 하는 함수인반면,
함수 sigmoid_2는 std에 포함된 자연상수e를 제곱함수 pow를 통해 제곱합니다.

실제로 아래 코드를 실행시켜보면은 모두 0과 1사이값으로 수렴하는것을 보실 수 있습니다.

#include <cmath>
#include <iostream>

double sigmoid_1(double z){
	return (1 / (1 + std::exp(-z)));
}

double sigmoid_2(double z){
	return (1 / (1 + std::pow(std::numbers::e, -z)));
}

int main() {
	std::cout.precision(13);
	std::cout << std::fixed << "(-10)Sigmoid_1: " << sigmoid_1(-10) << "\n(-10)Sigmoid_2: " << sigmoid_2(-10) << '\n';
	std::cout << std::fixed << "(10)Sigmoid_1: " << sigmoid_1(10) << "\n(10)Sigmoid_2: " << sigmoid_2(10);
}

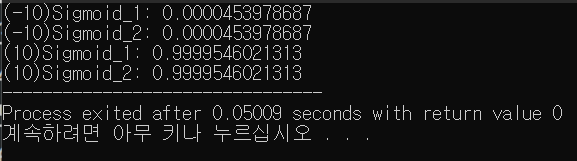
위 그림처럼 수가 아무리 작던 크던 모두 0과 1사이값안에서만 놀고있습니다.

💎Cost와 Loss함수

이번에도 저번글과 똑같은 옵티마이저를 사용할것이기 때문에 기본적으로 Cost를 계산하는 방법은 저번글과 같습니다.

저번에는 b(bias)의 고려없이 그냥 W(weight)만을 고려했습니다.
(아래 그림)

하지만 이번에는 좀더 정확한 값에 근접하기 위하여 편향(bias)도 고려할것입니다.
(아래 그림)

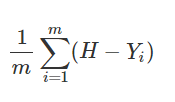
우선 위와 같은 공식이 어떻게 구성되어있는지는 저번글에서 설명했으니 이부분은 스킵하겠습니다.

다음은 로지스틱회귀의 loss function을 구하는 방법입니다.
머신러닝에서 값이 들어오면 실제값과 얼마만큼 유사한지의 기준이 필요한데 이때 사용하는것이 손실함수(loss function)입니다.

로지스틱회귀에서 사용될 손실함수는 다음과 같습니다.

y가 0이 들어올때는 $-log(1 - f(s_{1}))$이 실행되고,
y가 1이 들어올때는 $-log(f(s_{1}))$이 실행됩니다.

이제 이 함수를 실제 C++코드로 옮겨보겠습니다.

#include <cmath>
#include <iostream>

double loss(double hypothesis, double y){
	return (-y * std::log(hypothesis) - (1 - y) * std::log(1 - hypothesis));
}

int main() {
	std::cout.precision(13);
	for(double i=0;i<1;i+=0.1){
		std::cout << std::fixed << "(0)Loss: " << loss(i, 0.0) << '\n';
		std::cout << std::fixed << "(1)Loss: " << loss(i, 1.0) << "\n\n";
	}
}

위 소스코드를 실행시켜보면,

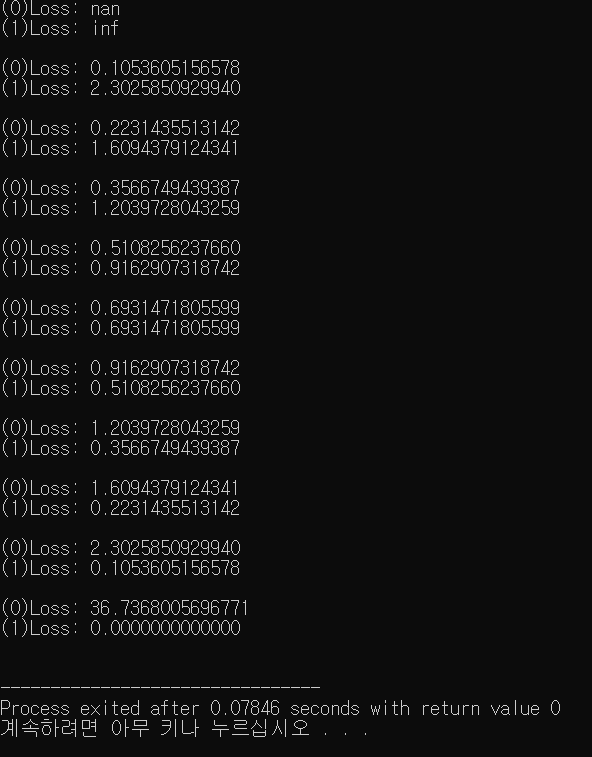
당연한 이야기지만, 실제로 y에 0이 들어갔을때와 1이 들어갔을때 다른값을 내놓게됩니다.

이제 마지막으로 이런것들을 바탕으로 로지스틱회귀를 구현해보겠습니다.

🔮소스코드

#include <iostream>
#include <vector>
#include <cmath>

using dataType = double;
constexpr double learning_rate = 1e-2;

// 시그모이드 함수
double sigmoid(double z){
	// https://www.HostMath.com/Show.aspx?Code=%5Cfrac%7B1%7D%7B1%20%2B%20e%5E%7B-z%7D%7D
	return 1.0 / (1.0 + std::exp(-z));
}

// 경사하강법
double GradientDescent(std::vector<dataType>& X, std::vector<dataType>& Y, double& W, double& b, double lr){
	const int m = Y.size();
	double loss = 0, dW = 0, db = 0;
	
	if(m != X.size()) throw std::runtime_error("The sizes of X and Y are not right");
	
	// cost function
	for(int i=0;i<m;++i){
		// Hypothesis
		double H = sigmoid(W * X[i] + b);
		
		dW += (H - Y[i]) * X[i];
		db += H - Y[i];
	}
	
	// https://www.HostMath.com/Show.aspx?Code=%5Cfrac%7B1%7D%7Bm%7D%5Csum_%20%7Bi%3D1%7D%5Em(H%20-%20Y_%7Bi%7D)%20%5Ccdot%20X_%7Bi%7D
	dW = dW / m;
	
	// https://www.HostMath.com/Show.aspx?Code=%5Cfrac%7B1%7D%7Bm%7D%5Csum_%20%7Bi%3D1%7D%5Em(H%20-%20Y_%7Bi%7D)
	db = db / m;
	
	// loss function
	for(int i=0;i<m;++i){
		// hypothesis
		double H = sigmoid(W * X[i] + b);
		
		loss += (Y[i] * std::log(H) + (1 - Y[i]) * std::log(1 - H));
	}
	
	// weight and bias Update
	W = W - lr * dW;
	b = b - lr * db;
	
	// https://www.HostMath.com/Show.aspx?Code=-%5Cfrac%7B1%7D%7Bm%7D%5Csum_%20%7Bi%3D1%7D%5Em%5By%20%5Ccdot%20%5Clog_%7B%7D%7BH_%7Bi%7D%7D%20%2B%20(1%20-%20y)%20%5Ccdot%20%5Clog_%7B%7D%7B1%20-%20H_%7Bi%7D%7D%5D
	loss = loss * -1 / m;
	
	return loss;
}

// 로지스틱회귀
void LogisticRegression(std::vector<dataType>& X, std::vector<dataType>& Y, double& W, double& b, int epochs, double lr){
	int printTry = epochs / 10;
	
	for(int i=0;i<epochs;++i){
		double loss = GradientDescent(X, Y, W, b, lr);
		if(i % printTry == 0) std::cout << "Weight: " << W << ", Bias: " << b << ", Loss: " << loss << '\n';
	}
}

// 값 예측
double predict(double& W, double& b, dataType X){
	return (sigmoid(W * X + b) < 0.5) ? 0 : 1;
}

int main() {
	std::vector<dataType> X =
	{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
	std::vector<dataType> Y =
	{ 1, 1, 1, 1, 1, 0, 0, 0, 0, 0 };
	double W = 12; // random value
	double b = 12; // random value
	
	// train 5000 times
	LogisticRegression(X, Y, W, b, 5000, learning_rate);
	
	// prediction
	const int nX = 11;
	std::cout << "Prediction: " << predict(W, b, nX);
}

네... 뭔가 심플하고, 저가 언급했던것들이 중간중간에 보입니다.
자세한 공식을 보고싶으신분들은 저가 주석에다가 걸어논 링크를 클릭해주세요.

이 코드는 1~10까지의 수를 기계에게 학습시켜서 임의의 수를 내놓았을때 그 결과가 1인지 0인지 예상하도록 기계에게 시키는 내용입니다.

위 소스코드에서는 저는 11번째에는 뭐가 나올까 기계에게 물어보니,

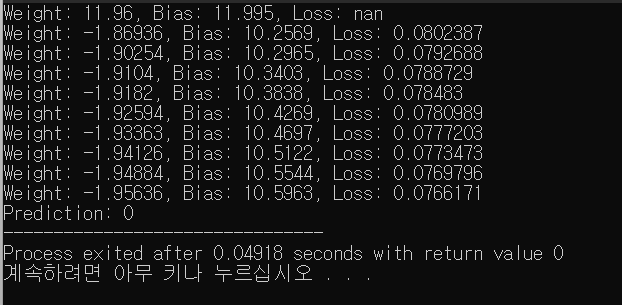
0이 나올것같다네요.

하지만, 위와 같이 단순히 한개의 입력값만으로 판단할 수 없는 문제도 존재할것입니다.

따라서 우리는 이제부터 여러개의 입력값으로부터 어떻게 로지스틱회귀를 수행하도록 하는지에 대하여 알아보겠습니다.

🔪다중입력 적용하는법

💎행렬곱셈

우선 머신러닝에서 기본적으로 다중입력에 관한 개념을 이해하기 이전에, "행렬곱셈"이라는것에 관하여 알아보겠습니다.

저가 몇일전에 티스토리에다가 관련이론과 실습내용을 올려놨는데, 여기서도 간단하게 설명하자면 아래와 같은 두 행렬이 있다고 가정합시다.

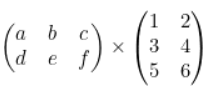
위 그림에서의 두 행렬을 곱하는것이 행렬곱셈입니다.
실제로 위 식은 아래 그림처럼 곱해집니다.

좀 더 자세한 내용을 알고싶으신분들은 위 티스토리 링크를 타고 들어가주시기 바랍니다.

행렬곱셈에서 또한 중요한 점이라고 한다면, 결과로써 나오는 행렬의 길이입니다.

자세히 보시면 각각 행렬의 크기를 (가로, 세로)로 한다면,
[3, 2] x [2, 3] = [2, 2]인것을 보실수가있고 이것을 문자로 표기하면 [a, b] x [c, d] = [b, c]가 됩니다.

이것을 실제 C++코드로 옮긴다면 다음과 같습니다.

#include <iostream>
#include <vector>

using ArrayType = double; 

/**
		@param (첫번째행렬, 세로길이1, 가로길이1, 두번째행렬, 세로길이2, 가로길이2)
*/
template<typename vecType>
std::vector<std::vector<vecType>> matmul(
		std::vector<std::vector<vecType>>& arr1, int row1, int col1,
		std::vector<std::vector<vecType>>& arr2, int row2, int col2){
			
	std::vector<std::vector<vecType>> result(row1, std::vector<vecType>(col2));
	
	for(int i=0;i<row1;++i){
		for(int j=0;j<col2;++j){
			vecType sum = 0.0;
			for(int k=0;k<row2;++k) sum += arr1[i][k] * arr2[k][j];
			result[i][j] = sum;
		}
	}
	
	return result;
}

int main() {
	const int ROW_1 = 2;
	const int COL_1 = 3;
	const int ROW_2 = 3;
	const int COL_2 = 2;
	
	std::vector<std::vector<ArrayType>> arr1 =
		{
			{ 1, 1, 3 },
			{ 3, 2, 1 },
		};
	
	std::vector<std::vector<ArrayType>> arr2 =
		{
			{ 1, 2 },
			{ 1, 1 },
			{ 1, 3 },
		};
	
	auto result = matmul<ArrayType>(arr1, ROW_1, COL_1, arr2, ROW_2, COL_2);
	
	for(int i=0;i<ROW_1;++i){
		for(int j=0;j<COL_2;++j){
			std::cout << result[i][j] << ' ';
		}
		std::cout << '\n';
	}
}

이제 이 행렬곱셈을 이용하여 다중입력을 통한 로지스틱회귀를 구현해보겠습니다.

🔮소스코드

#include <iostream>
#include <vector>
#include <cmath>

// input(X) type
using dataType = double;

// learning_rate = 0.001
constexpr double learning_rate = 1e-3;

/**
		@author https://mawile.tistory.com/202
		@param (첫번째행렬, 세로길이1, 가로길이1, 두번째행렬, 세로길이2, 가로길이2)
*/
template<typename vecType>
std::vector<std::vector<vecType>> matmul(
		std::vector<std::vector<vecType>> arr1, int row1, int col1,
		std::vector<std::vector<vecType>> arr2, int row2, int col2){
			
	std::vector<std::vector<vecType>> result(row1, std::vector<vecType>(col2));
	
	for(int i=0;i<row1;++i){
		for(int j=0;j<col2;++j){
			vecType sum = 0.0;
			for(int k=0;k<row2;++k) sum += arr1[i][k] * arr2[k][j];
			result[i][j] = sum;
		}
	}
	
	return result;
}

/**
		@brief sigmoid function
*/
double sigmoid(double z){
	// https://www.HostMath.com/Show.aspx?Code=%5Cfrac%7B1%7D%7B1%20%2B%20e%5E%7B-z%7D%7D
	return 1.0 / (1.0 + std::exp(-z));
}

/**
		@brief gradient descent
*/
std::vector<double> GradientDescent(std::vector<std::vector<dataType>>& X, std::vector<std::vector<dataType>>& Y, std::vector<std::vector<dataType>>& W, double& b, double lr){
	const int m = Y.size() * W[0].size(); // The length of the arrangement.
	const int row1 = X.size(); // axis = 0
	const int col1 = X[0].size(); // axis = 1
	const int row2 = W.size(); // axis = 0
	const int col2 = W[0].size(); // axis = 1
	
	std::vector<double> lossList; // Arrangement of the loss function result.
	
	if(m != X.size() *  W[0].size()) throw std::runtime_error("The sizes of X and Y are not right");
	
	// matrics multiplication
	auto matmulWX = matmul(X, row1, col1, W, row2, col2);
	
	// calulate dW and db
	for(int i=0;i<row1;++i){
		double loss = 0, dW = 0, db = 0;
		
		for(int j=0;j<col2;++j){
			// Hypothesis
			double H = sigmoid(matmulWX[i][j] + b);
			
			// sigma dW
			dW += (H - Y[i][j]) * X[i][j];
			
			// sigma db
			db += H - Y[i][j];
		}
		
		// https://www.HostMath.com/Show.aspx?Code=%5Cfrac%7B1%7D%7Bm%7D%5Csum_%20%7Bi%3D1%7D%5Em(H%20-%20Y_%7Bi%7D)%20%5Ccdot%20X_%7Bi%7D
		dW = dW / m; // m = row1 * col2
		
		// https://www.HostMath.com/Show.aspx?Code=%5Cfrac%7B1%7D%7Bm%7D%5Csum_%20%7Bi%3D1%7D%5Em(H%20-%20Y_%7Bi%7D)
		db = db / m; // m = row1 * col2
		
		// loss function
		for(int j=0;j<col2;++j){
			// hypothesis
			double H = sigmoid(matmulWX[i][j] + b);
		
			loss += (Y[i][j] * std::log(H) + (1 - Y[i][j]) * std::log(1 - H));
		}
		
		for(int i=0;i<row2;++i){
			for(int j=0;j<col2;++j){
				// weight and bias Update
				W[i][j] = W[i][j] - lr * dW;
				b = b - lr * db;
			}
		}
		
		// https://www.HostMath.com/Show.aspx?Code=-%5Cfrac%7B1%7D%7Bm%7D%5Csum_%20%7Bi%3D1%7D%5Em%5By%20%5Ccdot%20%5Clog_%7B%7D%7BH_%7Bi%7D%7D%20%2B%20(1%20-%20y)%20%5Ccdot%20%5Clog_%7B%7D%7B1%20-%20H_%7Bi%7D%7D%5D
		loss = loss / -m; // m = row1 * col2
		
		lossList.push_back(loss);
	}
	
	return lossList;
}

void LogisticRegression(std::vector<std::vector<dataType>>& X, std::vector<std::vector<dataType>>& Y, std::vector<std::vector<dataType>>& W, double& b, int epochs, double lr){
	int printTry = epochs / 10; // Print epochs as many times as the value divided by 10.
	
	for(int i=0;i<epochs;++i){
		auto loss = GradientDescent(X, Y, W, b, lr);
		if(i % printTry == 0){
			std::cout << "Weight: ";
			for(int i=0;i<W.size();++i) for(int j=0;j<W[0].size();++j) std::cout << W[i][j] << " ";
			std::cout << "\nBias: " << b << "\nLoss: ";
			for(int j=0;j<loss.size();++j) std::cout << loss[j] << ' ';
			std::cout << "\n\n";
		}
	}
}

std::vector<std::vector<int>> predict(std::vector<std::vector<dataType>>& W, double& b, std::vector<std::vector<dataType>> X){
	std::vector<std::vector<int>> result;
	
	// matrics multiplication
	auto matmulWX = matmul(X, X.size(), X[0].size(), W, W.size(), W[0].size());
	
	for(int i=0;i<X.size();++i){
		result.push_back(std::vector<int>());
		
		for(int j=0;j<W[0].size();++j){
			result[i].push_back((sigmoid(matmulWX[i][j] + b) < 0.5) ? 0 : 1);
		}
	}
	
	return result;
}

void printPrediction(std::vector<std::vector<int>> prediction){
	std::cout << "Prediction: ";
	for(int i=0;i<prediction.size();++i){
		for(int j=0;j<prediction[i].size();++j){
			std::cout << (prediction[i][j] == 0 ? "시험불합격예측..ㅠ" : "시험합격예측~!!") << ' ';
		}
		std::cout << '\n';
	}
}

double Accuracy(std::vector<std::vector<dataType>>& X, std::vector<std::vector<dataType>>& Y, std::vector<std::vector<dataType>>& W, double& b){
	// matrics multiplication
	auto matmulWX = matmul(X, X.size(), X[0].size(), W, W.size(), W[0].size());
	double sum = 0.0;
	
	for(int i=0;i<X.size();++i){
		for(int j=0;j<W[0].size();++j){
			// Hypothesis
			double H = sigmoid(matmulWX[i][j] + b);
			sum += (((H < 0.5) ? 0 : 1) == Y[i][j] ? 1 : 0);
		}
	}
	
	// 1/m * sigma((H < 0.5 ? 0 : 1) == Y[i][j] ? 1 : 0);
	return sum / static_cast<double>(X.size() * W[0].size());
}

int main() {
	srand(time(0));
	const dataType random_value = rand() % 20;  // random value
	
	std::vector<std::vector<dataType>> X =
	{
		{ 1.5, 2.2, 1.1 },
		{ 1.2, 3.5, 1.5 },
		{ 2.2, 2.9, 1.8 },
		{ 2.6, 2.1, 1.9 },
		{ 2.9, 1.1, 3.6 },
		{ 3.9, 0.5, 3.2 },
		{ 4.3, 4.9, 4.1 },
	};
	std::vector<std::vector<dataType>> Y =
	{
		{ 1 },
		{ 1 },
		{ 1 },
		{ 1 },
		{ 0 },
		{ 0 },
		{ 0 },
	};
	std::vector<std::vector<dataType>> W =
	{
		{ random_value },
		{ random_value },
		{ random_value },
	};
	double b = random_value;
	
	// train 30000 times
	LogisticRegression(X, Y, W, b, 30000, learning_rate);
	
	// prediction
	std::vector<std::vector<dataType>> nX = { { 3.2, 2.15, 1.9 } };
	
	printPrediction(predict(W, b, nX));
	
	auto accuracy = Accuracy(X, Y, W, b);
	
	std::cout.precision(12);
	std::cout << std::fixed  << "\nAccracy: " << accuracy << '(' << int(accuracy * 100) << "%)";
}

우선 저는 시험점수로 예를들겠습니다.
각각 1.5등급, 2.2등급, 1.1등급을 받으면 합격(1)한다고 정의하고,
2.9등급, 1.1등급, 3.6등급을 받으면 불합격(0)한다고 등등 이런식으로 정의했습니다.

그리고! 만약 3.2등급, 2.15등급. 1.9등급을 받으면 시험에 합격할까? 에관하여 기계한테 물어보니 시험에 불합격한다고 나왔습니다.

다음은 소스코드에 관한 부가적인 설명에 관하여 이야기하겠습니다.

🔑코드설명

• 라이브러리 참조

#include <iostream>
#include <vector>
#include <cmath>

위 라이브러리는 c++에서 공식으로 지원하는 공식라이브러리 입니다.
각각 입출력, 수학관련 레퍼런스, 배열을 사용할 수 있도록 포함시켜줍니다.

• 새로운 타입선언

  // input(X) type
  using dataType = double;

저는 데이터에 타입을 쉽게 바꾸기위해, 따로 dataType이라는 타입을 정의했습니다.

왜냐하면, 저가 입력하려는 데이터가 실수에서 정수로 바꾸고싶을때 위의 dataType을 int로만 바꾸면 모두 바꿀수있기때문입니다.

• 학습률

  // learning_rate = 0.001
  constexpr double learning_rate = 1e-3;

학습률은 0.001로 설정했습니다.
너무 작게설정하면 학습을 너무 많이해야하고(학습시간 증가),
너무 크게설정하면 학습이 제대로 되지않습니다(학습 불안정).

• 전체크기 m

  const int m = X.size() * W[0].size();

전체크기가 위와 같이 되어있는 경우또한 행렬곱셈에서 알아볼수있는데,

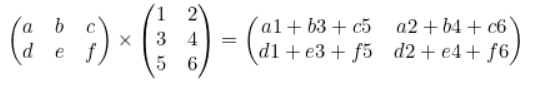
먼저 X.size()는 위 그림에서 첫번째행렬의 세로길이를 나타내구요,
W[0]는 위 그림에서 두번째행렬의 가로길이를 나타냅니다.

즉, 행렬곱셈의 결과로써 나오는 행렬의 넓이가 m이 되는거죠.

• 정확성 검사

for(int i=0;i<X.size();++i){
	for(int j=0;j<W[0].size();++j){
		// Hypothesis
		double H = sigmoid(matmulWX[i][j] + b);
		sum += (((H < 0.5) ? 0 : 1) == Y[i][j] ? 1 : 0);		}
}
	
// 1/m * sigma((H < 0.5 ? 0 : 1) == Y[i][j] ? 1 : 0);
return sum / static_cast<double>(X.size() * W[0].size());

정확성검사는 저가 위에서 언급하지 않은 내용이기 때문에 언급하자면

예를들어 시그모이드함수에서 나온 값이 0인지 1인지 판단하면서 sum에 모두 더한후 결과값행렬(X.size() * W[0].size())의 크기만큼 나눠줍니다.

보기좋게 수식으로 표현하자면..
$\frac{1}{m} \cdot \sum_{i=1}^m[sum_{i}]$ 입니다.

🔪마무리

💎느낀점

이번에도 C++로 로지스틱회귀를 직접 제로부터 구현해보면서 좀더 성장한것같다.
중간에 행렬곱셈이랑 로지스틱회귀 섞어가면서 만드는데,
머리과부화 걸려서 터질뻔했다..

결과적으로는 성취감 만땅이였고, 재미있었다 ...

💎마치며...

궁금한 부분있으면 댓글로 질문주세요!
그럼 안녕~~~~