🔪소개및 개요
💎개요
안녕하세요!
파이썬에서 tensorflow의 keras로 object detection, mnist를 이용하여 손글씨 학습하기, 등등 softmax층과 relu층을 이용한 다양한 실습을 하면서 흥미를 찾아가는 머신러닝 입문자입니다.
최근에 경사하강법에 관하여 c++에서도 갑자기 구현해보고 싶어서 방금 만들어봤는데,
진짜로 이론대로 그대로 하니까 되더라구요..!!!ㅋㅋㅋㅋㅋ
신기해서 직접 쓴 경사하강법 코드 올립니다.
코드를 즉석으로 짜고 올려서 코드는 매우 더럽습니다. (ㅈㅅ합니다..ㅎㅎ..!)
💎환경
- 통합개발환경: DevCpp
- 언어: C++17
- 운영체제: Windows11 Home
- 컴파일러: g++
🔪경사하강법
💎소스코드
// 아래 코드는 10번째까지의 값을 바탕으로 11번째의 값을 예측하는 선형회귀 코드입니다.
#include <iostream>
#include <vector>
#include <cmath>
constexpr double learning_rate = 1e-2;
double GradientDescent(std::vector<double>& X, std::vector<double>& Y, double& W){
const int m = Y.size();
double cost = 0, loss = 0;
if(m != X.size()) throw std::runtime_error("The sizes of X and Y are not right");
// cost function
for(int i=0;i<m;++i){
// Hypothesis
double H = W * X[i];
cost += (H - Y[i]) * X[i];
}
cost = cost / m;
// W assignment
W = W - (learning_rate * cost);
// loss function
for(int i=0;i<m;++i){
// Hypothesis
double H = W * X[i];
loss += std::pow(H - Y[i], 2);
}
return loss;
}
double predict(double& W, double X){
return (W * X);
}
int main() {
std::vector<double> X =
{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
std::vector<double> Y =
{ 1110, 2220, 3330, 4440, 5550, 6660, 7770, 8880, 9990, 11100 };
double W = 1; // random value
// train 30 times
for(int i=0;i<30;++i) std::cout << "loss: " << GradientDescent(X, Y, W) << ", weight: " << W << '\n';
// prediction
const int predictionX = 11;
std::cout << "prediction: " << predict(W, predictionX);
}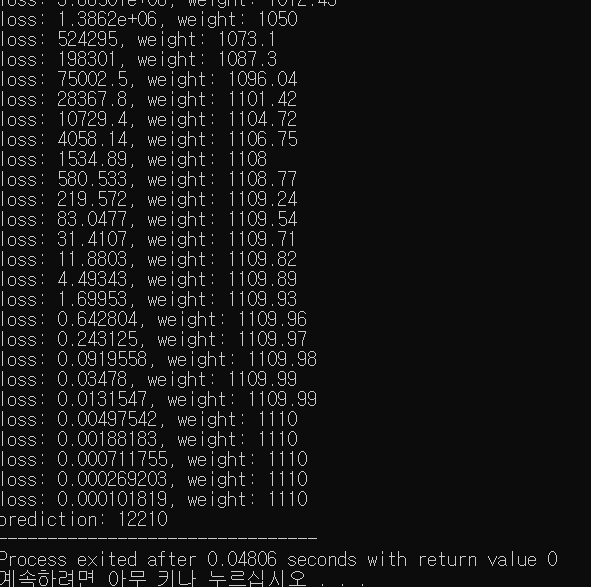
와우~! 12210이 나왔습니다!
💎이론및 설명
우선 아래그림은 위 소스코드에서 사용한 cost function을 미분한 공식입니다.
좀 기초적인 이야기지만, 미분한 공식을 사용한 이유는 특정위치에서의 기울기를 구하기위해서입니다.
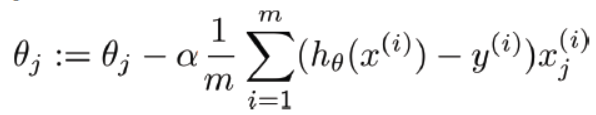
우선 a는 learning rate입니다.
경사하강법은 cost를 줄여나감으로써 최적의 W(그림에서는 오메가)를 찾는 알고리즘입니다.
이때 a는 그 cost의 기울기를 얼마만큼씩 줄여나갈것이냐를 정하는 값입니다. 저는 위코드에서는 1e-2를 줬습니다.
보통 머신러닝을 하다보면은 1e-2에서 1e-5사이로 줍니다.
이게 값을 적게 주면 W가 정교해지지만, 그만큼 학습해야될 횟수가 많아지죠.
반대로 값을 크게주면 학습은 적게해도 되지만, 그만큼 정확성(Accuracy)이 떨어집니다.
h는 hypothesis라고 해가지고, W와 Xi를 곱한값입니다.
bias는 편의성을 위해서 위 소스코드에는 포함하지 않았습니다.
위 식을 여러번씩 실행하는 과정을 우리는 "학습시킨다" 라고합니다.
그렇게 학습되서 나온 W(weight)를 바탕으로 내가 알고자하는 Xi와 곱해주면,
그것이 LinearRegression(선형회귀)이/가 되는겁니다.
loss function은 일반적으로 미분되지않은 경사하강법공식에서 m을 나누지않은 공식입니다.
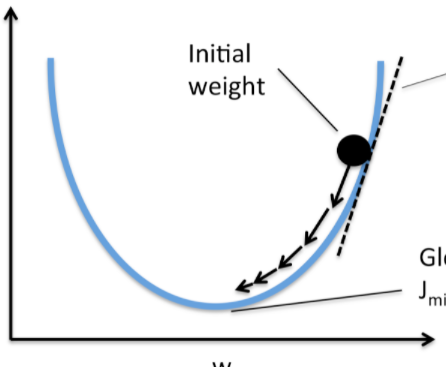
마지막으로 저기서 W(제일 위 그림에서는 오메가)를 빼는 이유를 수학적으로 설명하자면, 기울기를 조금씩 줄여나가기위함입니다.
그냥 쉽게생각하시면되는데, 만약 a와 cost function의 곱한 결과가 음수(W - (a cost))라면 저기서 W는 최종적으로 양수(W + (a cost))의 방향으로 갑니다.
반대로, a와 cost function의 곱한 결과가 양수(W - (a cost))라면 저기서 W는 최종적으로 음수(W - (a cost))의 방향으로 갑니다.
그러면 그 기울기는 점점 그래프의 중심점에 모이겠죠??
💎정리
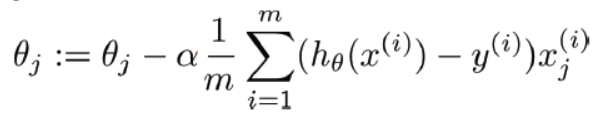
- 여러번 학습하는이유: cost를 최적화하기 위해서.
- 위 식에서 W(오메가j)를 뺀이유: 현재기울기가 양수면은 음수방향으로 더하고, 음수면은 양수방향으로 더하기위함.
- 위 식에서 a가 의미하는 것: 그래프에서 기울기를 얼마만큼씩 줄여나갈것인지 그 크기를 정하는것.
- 위 식에서 h가 의미하는것: W * Xi
- 위 식에서 :=는 무엇인가?: 크게 신경쓰지않아도된다. 그냥 왼쪽값에 대입한다는 의미.
🔪마치며...
다음에는 로지스틱회귀도 구현해보겠습니다! 오예!
궁금한 부분있으시면 댓글로 질문 부탁드립니다.

