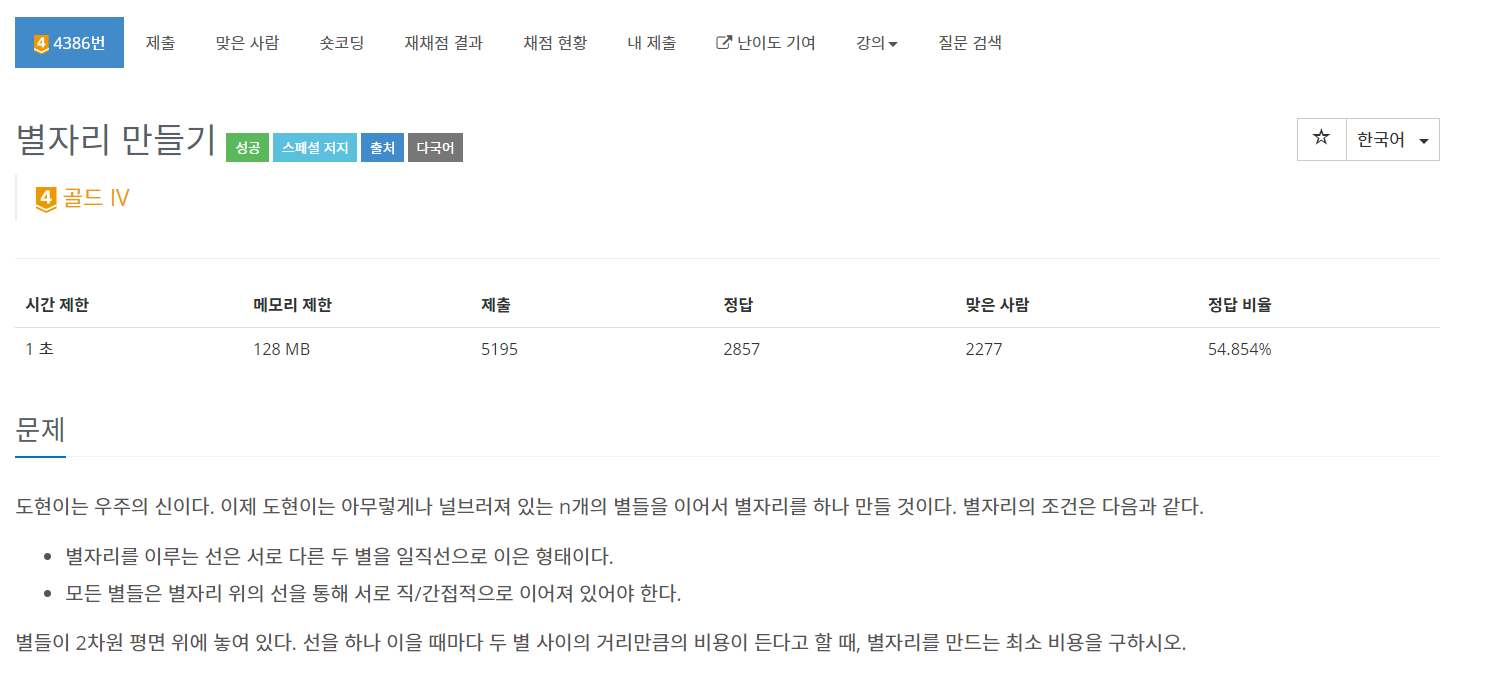
💉문제 내용

문제 풀러가기

💉입출력

🧺입력
첫째 줄에 별의 개수 n이 주어진다. (1 ≤ n ≤ 100)
둘째 줄부터 n개의 줄에 걸쳐 각 별의 x, y좌표가 실수 형태로 주어지며, 최대 소수점 둘째자리까지 주어진다. 좌표는 1000을 넘지 않는 양의 실수이다.

🧺출력
첫째 줄에 정답을 출력한다. 절대/상대 오차는 10-2까지 허용한다.

🔋예제 입출력

🔮예제 입력

3
1.0 1.0
2.0 2.0
2.0 4.0

🔮예제 출력

3.41

💉문제 분석

🔋분류

최소 스패닝 트리, 피타고라스의 정리

🔋난이도

골드IV

💉문제 풀이

🔋해법

이 문제는 피타고라스의 정리랑 MST만 알고계시면, 쉽게 풀 수 있는 문제입니다.
입력부분에 arr라는 임시배열을 만들어서 x, y좌표를 저장하게 한다음,
2중 for문과 피타고라스의 정리를 사용하여, 기존 x, y좌표말고 비용도 추가된 adj라는 배열을 만들었습니다.

그다음은 일반적인 MST라서 딱히 어려울건 없었습니다.

🔋소스코드

#include <bits/stdc++.h>

//Static variables
constexpr int MAX = 101;
constexpr int INF = 987654321;

struct pt {
	float a, b, c;

	bool operator<(pt p) {
		return c < p.c;
	}
};

//AlgoCapsule
class AlgoCapsule {
public:
	void Run() {
		Input();
		Solve();
		Output();
	}

	void Input() {
		std::cin >> N;

		for (int i = 0; i < N; ++i) {
			float x, y;
			std::cin >> x >> y;
			arr.push_back({ x, y, 0 });
		}

		for (int i = 0; i < N - 1; ++i) {
			for (int j = i + 1; j < N; ++j) {
				adj.push_back({ i, j,
				std::sqrt((int)std::pow((int)std::abs(arr[i].a - arr[j].a), 2) + (int)std::pow((int)std::abs(arr[i].b - arr[j].b), 2)) });
			}
		}
	}

	void Solve() {
		for (int i = 0; i < N; ++i) parent[i] = i;

		std::sort(adj.begin(), adj.end());

		for (int i = 0; i < adj.size(); ++i) {
			if (getParent(adj[i].a) != getParent(adj[i].b)) {
				result += adj[i].c;
				Union(adj[i].a, adj[i].b);
			}
		}
	}

	int getParent(int x) {
		if (parent[x] == x) return x;
		return parent[x] = getParent(parent[x]);
	}

	void Union(int a, int b) {
		a = getParent(a);
		b = getParent(b);

		if (a < b) parent[b] = a;
		else parent[a] = b;
	}

	void Output() {
		std::cout << result;
	}



	AlgoCapsule() { }
private:
	int parent[MAX];
	std::vector<pt> arr, adj;
	float result = 0;
	int N;
};

//Module Entry
int main() {
	std::ios_base::sync_with_stdio(0);
	std::cin.tie(0);
	std::cout.tie(0);

	AlgoCapsule AC;
	AC.Run();

	return 0;
}

쉬워서 크게 재미있진않았습니다.
풀고 자고일어나서 포스팅하는것때문에 13시간 전입니다.

💉마치며...

궁금한 부분있으시면 댓글로 질문주세요~