Why are Sensitive Functions Hard for Transformers?(2024)

0.0 Abstract

트랜스포머는 자연어 처리와 기타 다양한 분야에서 뛰어난 성능을 보여주었지만, PARITY와 같은 민감도가 높은 이진 함수를 학습하는 데 어려움을 겪습니다. 이 논문은 트랜스포머의 구조적 한계와 학습 편향을 수학적으로 분석하여, 트랜스포머가 민감도가 높은 함수를 학습하기 어려운 이유를 설명합니다.

주요 발견은 다음과 같습니다:

• 민감도가 높은 함수는 트랜스포머의 Layer Normalization 계수와 파라미터 크기가 비정상적으로 커야만 학습 가능하다는 점.
• 민감도와 모델의 손실 지형(Loss Landscape)의 날카로움(Sharpness)이 학습 최적화 과정에 직접적으로 영향을 미친다는 점.
• 기존의 Lipschitzness 이론을 확장하여 트랜스포머의 평균적 및 확률적 학습 경계를 수학적으로 도출.

결과적으로, 트랜스포머는 민감도가 낮은 함수에 대해선 강력한 학습 및 일반화 능력을 보이지만, 민감도가 높은 함수에서는 구조적 제약으로 인해 학습에 실패할 가능성이 높음을 시사합니다.

---

1.0. Introduction

트랜스포머는 주로 자연어 처리(NLP)와 이미지 처리 분야에서 성공을 거두며, 입력 데이터의 복잡한 관계를 모델링할 수 있는 강력한 표현력을 보여주었습니다. 하지만 일부 함수, 특히 PARITY와 같이 모든 입력 비트가 출력에 강하게 영향을 미치는 민감도가 높은 함수의 경우, 트랜스포머는 학습과 일반화에서 상당한 한계를 드러냅니다.

이 논문은 이러한 한계를 설명하기 위해 트랜스포머의 구조적 편향(Inductive Biases)과 손실 지형의 특성을 분석합니다. 특히 다음 두 가지 질문에 답을 제시합니다:

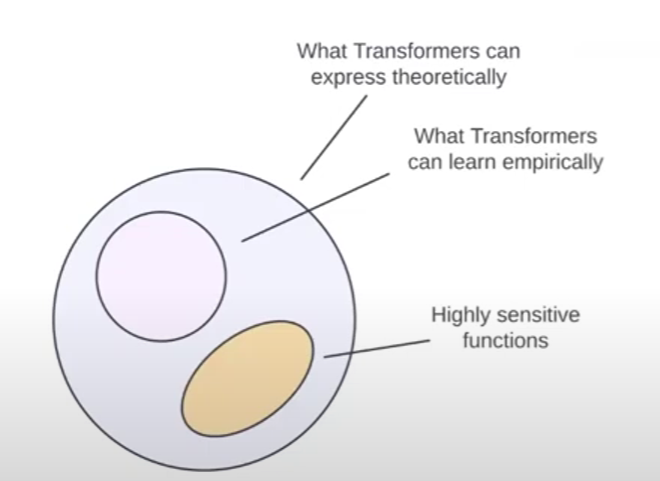
트랜스포머가 민감도가 높은 함수를 학습하기 어려운 이유는 무엇인가?
민감도와 관련된 학습 편향이 트랜스포머의 성능에 어떤 영향을 미치는가?
기존 연구는 트랜스포머의 강력한 표현 능력을 강조했지만, 이 논문은 단순한 표현 가능성만으로는 학습 가능성을 설명할 수 없음을 지적합니다. 즉, 표현력과 학습 가능성은 별개의 문제이며, 트랜스포머의 학습 능력은 loss landscape의 영향을 받습니다.

논문은 다음과 같은 주요 결과를 도출합니다:

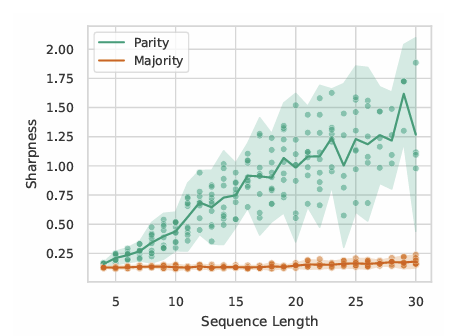
민감도가 높은 함수를 학습하려면, 트랜스포머의 Layer Norm 계수와 파라미터 크기가 기하급수적으로 증가해야 함.

• 이는 학습 최적화 과정에서 손실 지형의 극단적 날카로움을 유발해 학습을 어렵게 만듦.
• 트랜스포머는 민감도가 낮은 함수(MAJORITY, FIRST)에서 강한 학습 및 일반화 성능을 보이는 반면, PARITY와 같은 고민감도 함수에서는 학습 실패 가능성이 높음.

이 연구는 트랜스포머의 구조적 한계를 보다 깊이 이해하고, 향후 모델 설계 및 학습 전략 개선에 대한 방향성을 제공합니다.

---

2.0. Model of Transformers

이 논문에서 attention score를 어떻게 구했는지 알려주고 있습니다.
transformer는 n-길이의 binary input $x∈\{0, 1\}^n$을 받아 출력 $T(x)∈\{-1, 1\}$를 생성하는 모델입니다.

주요 구성요소는 다음과 같습니다.

1. 입력 임베딩 (Input Embedding)

   • 입력$x$를 $d$-차원의 연속 벡터 공간으로 변환:
     $y_i^{(0)} = W_E x_i + e_i$

2. 셀프 어텐션(Self-Attention)

• 어텐션 계산에 필요한 Query, Key, Value:
  $Q = W_Q \cdot y, \quad K = W_K \cdot y, \quad V = W_V \cdot y$

• 수식 정리:
  $a_{i, j}^{(k, h)}$ = $(K_{k,h}y_i^{(k-1)})^TQ_{k,h}y_i^{(k-1)}$

  j번째 token의 k-1번째 head의 key와 i번째 token의 k-1번째 head의 Query를 내적한 것이 $a_{i, j}^{(k, h)}$ 가 된다는 식입니다. 논문에서는 이것이 attention score라고 설명하고 있습니다.

주요 구성요소는 다음과 같습니다.

1. softmax 적용 -> attention weight만들기
2. $b_{i, h}^{(k)}$는 attention 결과
3. skip-connection 적용후 MLP layer통과

주요 구성요소는 다음과 같습니다.

1. Layer Normalization

2. Brittleness와 Layer Norm 계수 $N_i^{(k)}$의 관계
   $N_i^{(k)}$는 Layer Normalization의 계수입니다. 논문에서는 $N_i^{(k)}$가 input sensitivity, parameter space sharpness와 관계가 있다고 합니다.

• $N_i^{(k)}$ 값이 크다는 것
  민감도가 높은 함수 (PARITY 등)를 학습할 수 있도록 모델의 표현력을 증가시킴.
  하지만 파라미터 공간(parameter space)의 날카로움(Sharpness)이 커져 모델이 최적화 및 예측에서 불안정해질 수 있음

---

3.0. Average Sensitivity

3.1. 민감도의 정의

평균민감도(Average Sensitivity)란?

평균 민감도(Average Sensitivity)는 이진 함수가 입력의 변화, 특히 개별 비트의 변화에 얼마나 민감한지를 측정하는 지표입니다. 트랜스포머가 특정 함수(예: PARITY, MAJORITY)를 학습하는 데 얼마나 효과적인지 이해하기 위해 논문은 평균 민감도를 주요 분석 기준으로 삼습니다.

a. 개별 민감도(Sensitivity)

특정 입력 $x$와 함수 $f(x)$에 대해, 개별 민감도는 입력의 $i$-th bit를 바꿨을 때 출력 변화의 크기로 정의합니다.

• $x^{⊕i}$: 입력$x$의 $i$-th bit를 뒤집은 값
• $|f(x)-f(x^{⊕i})|^2$: 출력 변화의 크기를 나타냄

b. 평균 민감도(Average Sensitivity)

모든 가능한 입력 $x$에 대해 민감도를 평균 낸 값으로 정의됩니다:
$asn(f)$: 함수 $f$가 전체 입력 공간에서 얼마나 민감한지를 나타냄

3.2. 민감도와 학습 가능성의 관계

a. 높은 민감도를 가진 함수

• PARITY 함수
  $f(x) = \prod_{i=1}^n x_i$

  모든 입력 비트를 곱해여 출력하며, 입력 비트가 하나라도 바뀌면 출력이 완전히 반대가 된다.
  평균 민감도: $asn(f)$ = $n$. 입력 길이 $n$에 선형적으로 비례한다.
  결론: transformer가 학습하기 매우 어려운 함수임
  

b. 낮은 민감도를 가진 함수

• MAJORITY 함수
  $f(x) = \begin{cases} 1 & \text{if } \#\{i : x_i = 1\} > n / 2 \\ -1 & \text{otherwise} \end{cases}$
  입력 1의 개수가 -1보다 많으면 1을 반환함
  평균 민감도: $\text{asn}(f) = \Theta(\sqrt{n}). 비교적 낮음$
  결론: transformer가 학습하기 쉬운 함수

• FIRST 함수
  $f(x) = x_1$
  입력의 첫 번째 비트만 출력
  평균 민감도: $\text{asn}(f) = 1$. 매우 낮음
  결론: transformer가 학습하기 가장 쉬운 함수

3.3. 평균 민감도와 트랜스포머의 학습 편향

a. Low-Sensitivity Bias

• transformer는 평균 민감도가 낮은 함수(FIRST, MAJORITY)를 학습하는데 강한 편향을 가집니다.
• 이는 transformer의 설계가 입력 변화에 따른 출력의 안정성을 선호하기 때문입니다.

b. 높은 민감도의 함수 학습 한계

• 평균 민감도가 높은 함수(PARITY)는 transformer가 학습하기 어려운데, 이는 다음과 같은 요인 때문입니다.

1. Layer Norm 계수 증가
   높은 민감도를 표현하려면 Layer Norm 계수 $N_i^{(k)}$가 커져야 함.

2. Loss Landscape의 날카로움(Sharpness)
   높은 민감도는 손실 함수의 최소점 주변을 가파르게 만들어 최적화를 어렵게 만듬.

3. 일반화 성능 저하
   민감도가 높은 함수는 작은 변화에도 출력이 크게 달라져, 학습 데이터에 과적합될 위험이 큼.

💡 평균 민감도가 Transformer에 주는 시사점

• 표현력과 학습 가능성의 차이
  transformer는 이론적으로는 민감도가 높은 함수(PARITY)를 표현할 수 있지만, 실제 학습 가능성은 Loss Landscape, 최적화의 한계로 인해 제약을 받음

• 모델 설계와 학습전략
  transformer는 민감도가 낮은 함수에서 좋은 성능을 보이는 반면, 민감도가 높은 함수에서는 Layer Norm 계수 및 파라미터 크기를 늘려야만 학습이 가능함

---

4.0. Lower Bounds for Sensitive Functions

이 섹션에서는 민감도가 높은 함수(PARITY)를 트랜스포머로 표현하기 위해 필요한 구조적 제약과 학습의 어려움을 수학적으로 분석합니다. 트랜스포머가 민감도가 높은 함수를 학습하려면, 모델의 Layer Normalization 계수와 파라미터 노름(Parameter Norms)이 기하급수적으로 증가해야 하며, 이는 학습 안정성과 최적화 과정에서 심각한 문제를 초래합니다.

💡 주요 연구 질문

• 트랜스포머가 민감도가 높은 함수를 학습할 때, 필요한 구조적 자원의 최소 크기는 무엇인가?
• 이러한 제약이 손실 지형(Loss Landscape)과 학습 최적화에 어떤 영향을 미치는가?

4.1 Lipschitz 상수의 구성 요소

Lipschitz 상수

$C = \exp\left(4d \cdot \max_h \sum_{i=2}^L \|K_i^T Q_i\|_2^2 \right)$

각 기호의 의미

• C: Lipschitz 상수
• $K_i, Q_i$: transformer의 Key와 Query 행렬.
• $\|K_i^T Q_i\|_2^2$: Key-Quert 행렬의 스팩트럼 norm의 제곱
• d: 모델의 hidden dimention
• L: transformer layer의 개수
• $max_h$: Attention Head 중 최댓값을 계산

의미:

• Lipschitz 상수 C는 모델의 모든 층에서 Key-Query 행렬의 스펙트럼 노름이 클수록 기하급수적으로 증가합니다.
• 이는 민감도가 높은 함수를 표현하려면 각 층의 Key-Query 행렬의 크기가 중요하다는 점을 나타냅니다.

기존 Lipschitzness 경계

$s(f, x) \leq C \cdot \exp\left(4d \cdot \max_h \|K_1^T Q_1\|_2^2 \right) \cdot \epsilon^{L/2}$

각 기호의 의미

• $s(f, x)$: 특정 입력 $x$에서 함수 $f$의 민감도
• $\epsilon$: 안정성을 위한 작은 정규화 계수
• C: Lipschitz 상수
• $\|K_1^T Q_1\|_2^2$: 첫번째 층에서 Key-Query 행렬의 스팩트럼 norm의 제곱

의미:

• 특정 입력에 대해 민감도는 Key-Query 행렬의 스펙트럼 노름에 기하급수적으로 의존합니다.
• 민감도가 높은 함수를 학습하려면, Key-Query 행렬의 스펙트럼 norm이 기하급수적으로 증가해야 합니다.

💡 제안된 개선: 평균적 및 확률적 경계

• 기존 Lipschitzness 제약은 모든 입력에 대해 엄격한 상한을 제공했으나, 이는 현실적으로 너무 강한 제한일 수 있습니다.
• 논문에서는 대부분의 입력에 대해 더 완화된 경계를 제시합니다:
  특정 층(Key-Query 행렬의 스펙트럼 노름)에 의존하지 않고, 입력 길이에 따라 로그 계수(logarithmic factor)를 추가하여 경계를 개선합니다.

4.2 개선된 평균적 경계

수식
개선된 평균적 경계는 대부분의 입력에 대해 Lipschitzness가 더 완화된 형식으로 작동함을 보여줍니다.

$s(f, x) \leq C \cdot \log(n) \cdot \epsilon^{L/2}$

• $log(n)$: 입력 길이 $n$에 대한 로그 계수
• $C$: 기존의 Lipschitz 상수(이전 수식의 C와 동일).

해석

• 이 개선된 경계는 대다수 입력에 대해, 기존 경계에서 발생하던 지수적 증가($\exp\left(4d \cdot \max_h \|K_1^T Q_1\|_2^2 \right)$)를 로그 증가로 대체합니다.
• 이는 실제로 트랜스포머가 대부분의 입력에서 민감도를 더 낮게 유지할 수 있음을 알려줍니다.

Layer Norm과 민감도의 하한

트랜스포머가 민감도가 높은 함수를 표현하려면, 각 층의 Layer Norm 계수 $N_i^{(k)}$의 곱, 즉 Layer Norm Blowup이 커져야 합니다.

Layer Norm Blowup은 다음과 같이 정의됩니다.
$\text{Blowup}(x) = \prod_{k=1}^L \max_{w=1,\dots,n} \{1 + N_w^{(k)}(x)\}$

• $L$: transformer의 층 수.
• $n$: 입력 길이.

Blowup은 민감도가 높은 함수에서 출력이 얼마나 불안정하게 형성되는지를 보여주는 지표입니다.

Theorem 4: 민감도 $s(f, x)$는 Layer Norm의 Blowup에 의해 제한됩니다.

$s(f, x)\leq C \cdot \text{Blowup}(x)^2 + \text{(작은 값의 보정항)}$

즉, 민감도가 높은 함수를 표현하려면 Blowup이 반드시 커져야 합니다.

Corollary 5: 평균 민감도 $asn(f)$에 따라 Layer Norm Blowup의 기대값이 다음을 만족해야 합니다:

$C \cdot \mathbb{E}[\text{Blowup}(x)^2] \geq \frac{\text{asn}(f)}{\sqrt{n \log n}}$

평균 민감도가 입력 길이 𝑛에 비례하여 증가하면, Layer Norm Blowup 또는 파라미터 크기가 반드시 커져야 함을 의미합니다.

Corollary 5에 따르면

$C \cdot \mathbb{E}[\text{Blowup}(x)^2] = \Omega\left(\frac{\sqrt{n}}{\log n}\right) = \omega(1)$

최소의 증가량이 linear함수보다 크다.
-> 입력 길이가 증가할수록 Layer Norm Blowup이 기하급수적으로 증가해야 하므로, PARITY 학습이 점점 더 어려워집니다.

💡 이 섹션은 트랜스포머가 민감도가 높은 함수(PARITY)를 학습하기 위해 Layer Norm 계수와 파라미터 크기에서 극단적인 확장이 필요함을 이론적으로 증명합니다. 이는 다음을 시사합니다:

• PARITY와 같은 고민감도 함수는 트랜스포머에서 학습되기 어려운 함수입니다.
  트랜스포머의 학습 가능성은 단순한 표현력(Expressiveness) 이상의 구조적 한계(Layer Norm, 손실 지형 등)에 의해 제한됩니다.
• 트랜스포머는 민감도가 낮은 함수(MAJORITY, FIRST) 학습에 강한 편향을 가지며, 이는 모델 설계와 학습 전략에서 중요한 고려 사항이 됩니다.

5.0. Sensitive Transformers are Brittle

논문의 5장 "Sensitive Transformers are Brittle"는 Transformer 모델이 높은 민감도(sensitivity)를 가지는 함수를 학습할 때 나타나는 취약성과 불안정성 문제를 수식적으로 설명합니다. 이 섹션의 주요 요점과 관련 수식은 다음과 같습니다

5.1 높은 민감도와 매개변수 공간에서의 불안정성

논문에서는 Transformer 모델이 민감도가 높은 함수를 학습할 때, 매개변수의 작은 변화에도 예측 결과가 급격히 바뀌는 불안정한 최적화 상태(Sharp Minima)에 놓이게 됨을 보입니다. 이 현상은 다음의 수식을 통해 나타납니다.

평균 방향 예리함 (Average Direction Sharpness)

매개변수 벡터 $\theta$에 대해 Transformer $T_\theta$의 Average Direction Sharpness $L_{p, n}(T)$은 다음과 같이 표현됩니다.

$L_{\rho,n}(T) := \mathbb{E}_{x \in \{ \pm 1 \}^n} \mathbb{E}_{\|\Delta\|_2 = \rho} \left( T_{\theta + \Delta}(x) - T_{\theta}(x) \right)^2$

• $x$는 입력데이터
• Δ는 매개변수 공간에서 반경 ρ인 구(sphere) 내의 방향 벡터입니다.

이 식은 매개변수 공간에서 작은 변화가 모델 출력에 미치는 평균적인 변화를 측정합니다. 만약 특정 함수에 대해 $L_{p, n}(T)$가 크다면, 이는 Transformer 모델이 그 함수를 학습할 때 불안정하게 반응하며, 매개변수의 작은 변화에도 민감한 출력을 내놓게 된다는 것을 의미합니다.

5.2 민감도와 예리한 최소점 (Sharp Minima)

다음은 중요한 결과를 나타내는 수식으로, 높은 민감도를 가진 함수가 Transformer 모델의 Sharp Minima를 형성하는 이유를 설명합니다.

$\lim_{\rho \to 0} \liminf_{n \to \infty} L_{\rho,n}(T) \geq \liminf_{n \to \infty} \frac{\text{asn}(T_{\theta})}{2n} - L \exp(-\Omega(d))$

• $asn(T_\theta)$는 평균 민감도를 나타내며, 이는 Transformer가 특정 입력 길이에서 얼마나 민감하게 반응하는지를 나타내는 척도입니다.
• $L$과 𝑑는 Transformer의 레이어 수와 차원을 나타내며, 모델의 구조적 제약 조건을 의미합니다.

이 식은 입력 길이 𝑛이 커짐에 따라 평균 민감도가 높은 함수일수록 Transformer의 예리함(Sharpness)이 커진다는 사실을 나타냅니다. 이는 매개변수가 조금만 바뀌어도 모델의 예측이 크게 달라질 가능성을 내포합니다.

6.0 Implications (의미)

이 장에서는 Transformer 모델이 민감한 함수들을 학습할 때 나타나는 어려움과 그로 인해 발생하는 여러 현상에 대한 이론적 설명을 제시합니다.

핵심 요점은 다음과 같습니다:

• Difficulty of PARITY: PARITY와 같은 높은 민감도의 함수는 입력 길이가 길어질수록 학습이 더욱 어려워집니다. 이는 Transformer가 이러한 함수를 정확하게 일반화하려면 특정 매개변수 조합에 매우 의존하게 되어, 조그만 변화에도 모델이 불안정해지기 때문입니다.

• Length Generalization: Transformer가 민감도가 높은 함수에서 입력 길이에 따른 일반화에 실패하는 이유는, 예리한 최소점(Sharp Minima)을 찾지 못하는 경우 학습 과정에서 안정적인 일반화를 달성하기 어렵기 때문입니다.

• Intermediate Steps Reduce Sensitivity: 학습이 진행되는 동안 Transformer는 주어진 훈련 데이터에서 민감도를 최소화하려는 경향이 있으며, 이로 인해 일반화 과정에서 민감도가 낮은 함수로 편향될 가능성이 있습니다.

7.0 Experiments

실험 장에서는 6장에서 제시된 이론적 분석을 확인하기 위해 다양한 함수와 입력 길이에서 Transformer 모델의 민감도를 실험합니다.

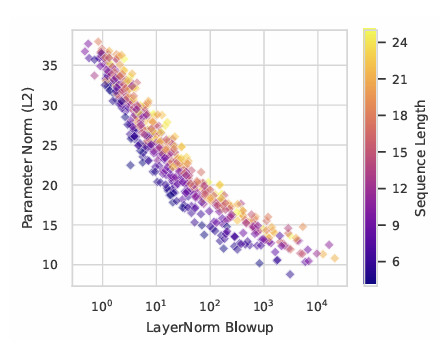
• Layer Norm Blowup 및 파라미터 크기: 실험을 통해 Layer Norm이 커지거나 파라미터가 커질수록 모델이 민감한 함수를 학습하는 데 더 효과적인 것을 발견했습니다.

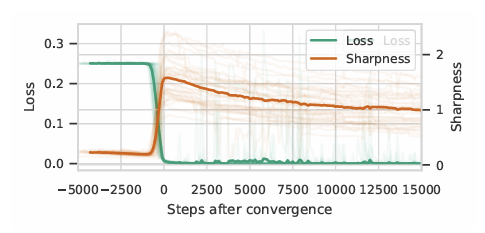
• Sharpness 측정: 민감도가 높은 함수일수록 모델의 최적화가 Sharp한 최소점에 도달하는 양상을 보이며, 이는 평균 방향 예리함(Average Direction Sharpness)을 측정함으로써 확인되었습니다.

• 길이 일반화: PARITY와 같은 함수에서 길이가 증가할수록 학습이 불안정해지고 일반화가 실패하는 현상을 실험적으로 확인했습니다.

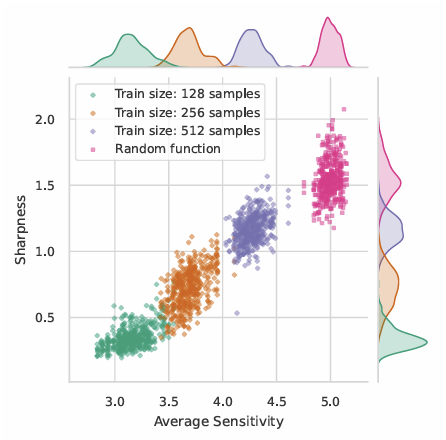
훈련 데이터의 크기가 작을수록 모델이 학습한 함수의 민감도가 낮아지는 경향을 보입니다.이는 모델이 데이터셋 외부에 대해 더 안정적으로 예측하려는 편향이 나타난 것으로 해석됩니다.

결론적으로, Figure 4는 Transformer가 훈련 데이터 크기에 따라 민감도를 최소화하는 방향으로 일반화하여, 민감도가 낮은 함수로 예측하는 경향을 실험적으로 보여준다고 생각합니다.

8.0 Conclusion

이 논문은 Transformer는 높은 민감성을 가진 input에 대해 sharp한 minima에서만 모델이 최적화 될 수 있음을 보여주는 논문이다.
종합적으로 봤을 때 이전에는 설명하지 못했던 transformer의 문제점을 loss landscape과 quantitative bound를 통해 증명을 하는 논문이다.

논문을 읽을때 Lipschitzness bounds에 대한 내용과 appendix b를 완벽하게 이해하지 못해서 관련 논문을 추후에 읽을 예정입니다.