[PL] Lexical Analysis : Sigma Representation

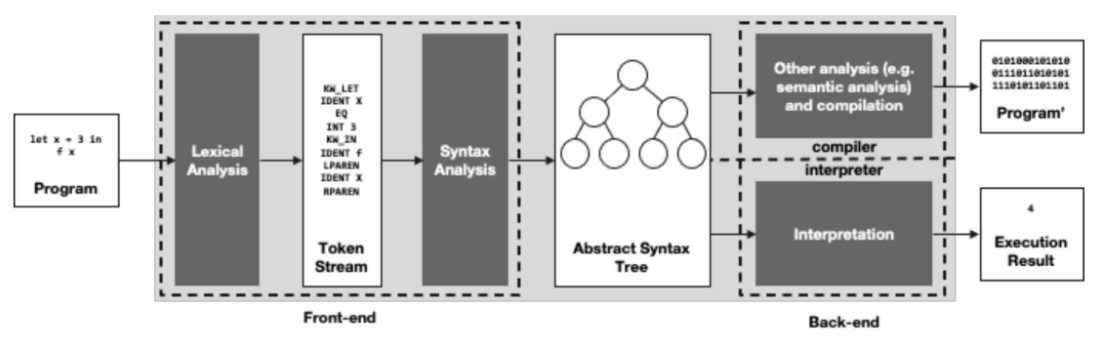
1. Higer Abstraction => 'TOKEN'

➡️ 영어는 알파벳과 특별한 문자들(!, ?, . 등)로 이루어져 있다. 그러나 우리가 영어를 읽을 때는 각각의 문자를 하나 하나 읽지 않고, 단어/문장/단락 단위로 읽는다.

ex) home을 읽을 때에 'h', 'o', 'm', 'e'로 읽는 것이 아니라 'home'으로 읽는다.

➡️ 프로그래밍 언어 역시 동일하다. 프로그래밍 언어도 알파벳과 특수한 문자들로 이루어져 있는데, 컴파일러는 각 문자별로 읽지 않고 '토큰' 단위로 읽는다.

✔️토큰이란?!

"패턴을 사용하여 정확하게 지정된, 문법적으로 의미 있는 최소 단위"

ex) == 은 하나의 토큰이고, <= 은 하나의 토큰이고, while 은 하나의 토큰이다.

ex) ocaml 의 프로그램 코드 "let x = 3 in f x"을 컴파일러가 lexical analysis 하면, 다음과 같이 변환된다.

KW_LET INDENT X EQ INT 3 KW_IN INDENT f LPAREN INDENT X RPAREN

➡️ 토큰은 정해진 '패턴'을 통해 만들어진다. Lexical Analyzer는 주어진 패턴에 따라 프로그램을 토큰의 형태로 만드는 역할을 한다. 그렇다면, 패턴은 어떻게 만들까?!

2. Language Syntax

➡️ 프로그래밍 언어는 분명하게 지정된 문법을 가지고 있어야 한다. 이 문법을 토대로 패턴을 적절하게 만들 수 있다.

문법이 명학하지 않을 경우에는 그 언어를 배우기 어려울 뿐만 아니라 컴파일러를 만들 수 없다.

✔️ 예시

이 예시에서 G 는 문법을, L은 주어진 문법을 통해 모든 유효한 문자열을 만들어 내는 함수를 의미한다.

Lexical Analyzer가 토큰을 만든다면, Syntax Analyzer는 프로그램이 올바른 문법으로 만들어져 있는지 확인한다. Syntax Analyzer는 'I have done the homework'와 같은 문법적 오류를 검사하는 역할을 하는 것이다.

3. Sigma Representation으로 나만의 언어 만들어 보기

1) 언어에 필요한 모든 Symbol을 정의해야 한다.

✔️ $\sum$ 을 이용하여 모든 Symbol을 정의한다.

Symbol 은 a, b, B, Q, 0, 5, ', '', ), _ ... 등등, 원하는 것을 정의할 수 있다.

2) Symbol들을 결합하여 만들어질 수 있는 모든 문자열들의 집합을 정의한다.

✔️ $\sum^*$ 는 $\sum$ 을 이용하여 만들어질 수 있는 모든 문자열의 집합이다.

▪️ 예시

$\sum$ = { a, b, c }
$\sum^*$ = { a, b, c, aa, aaa, ab, ac, ccc, bbb, ... }

▪️ 예시 2 : 알파벳들은 다양한 형태로 정의될 수 있다.

$\sum_{binary}$ = { 0, 1 }
$\sum_{digit}$ = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }
$\sum_{capital}$ = { A, B, C, D, E, .. Z }
$\sum_{lower-case}$ = { a, b, c, d, e, .. z }
$\sum_{alphanumeric}$ = { 0, .. 9, a .. z, A, .. Z }

3) 나만의 '집합 연산'(Set Operation)을 만들어 볼 수 있다.

✔️ 다음 3가지 Set Operation을 정의해 보자.

(1) Concatenation

$\sum_1$ $\sum_2$ = { xy | x $\in$ $\sum_1$ and y $\in$ $\sum_2$ }

▪️ 예시

$\sum_1$ = {a-z}, $\sum_2$ = {0-9} 일 때 $\sum_1$ $\sum_2$ = {a0, b8, z9 .. }

(2) Union

$\sum_1$ $\cup$ $\sum_2$ = { xy | x $\in$ $\sum_1$ or x $\in$ $\sum_2$ }

▪️ 예시
$\sum_1$ = {a-z}, $\sum_2$ = {0-9} 일 때 $\sum_1$ $\cup$ $\sum_2$ = {a, b, .. z, 0, 1, .. 9}

(3) Kleene Closure

$\sum^0$ = { $\epsilon$ }

$\sum^*$ = { X | X $\in$ $\epsilon$ or X $\in$ $\sum$ or x $\in$ $\sum$$\sum$ or ... }

▪️ 예시
$\sum$ = {0-9} 일 때 $\sum^*$ = { $\epsilon$, 1, 23, 531, 124, 9314 .. }

4) 내가 정의한 언어의 문자열은 알파벳의 유한한 Sequence이다.

따라서 알파벳 $\sum$ 으로 만들어질 수 있는 모든 가능한 문자열은 $\sum^*$ 이다.

✔️ A Language L over alphabet $\sum$ is a set of strings over $\sum$.

✔️ A Language L is a subset of $\sum^*$

▪️ 예시

$\sum^*_{binary}$ = { $\epsilon$, 0, 1, 00, 01, 00, 10, 11, 000 ... }

$\sum^*_{digit}$ = { $\epsilon$, 0, 1, .. 9, 00, .., 99, 0000 .. }

$\sum^*_{capital}$ = { $\epsilon$, A, .. Z, AA, .. ZZ, AAA, ..}

$\sum^*_{lower-case}$ = { $\epsilon$, a, .. z, aa, .. zz, aaa, ... }

4. 실습

1) $\sum_{binary}$ = { 0, 1 } 이라면, 01010001 은 $\sum^*_{binary}$ 에 속할까?

➡️ YES! 01010001 $\in$ $\sum^*_{binary}$

2) $\sum_{alphanumeric}$ = { 0, .. 9, a .. z, A, .. Z } 이라면, A0x7 은 $\sum_{alphanumeric}$에 속할까?

➡️ Yes!

3) A0x!7 은 $\sum_{alphanumeric}$ 에 속할까?

➡️ NO! Symbol ! 은 유효하게 정의된 symbol이 아니기 때문이다.

4) Email Address 를 표현하는 언어 'Lemail'을 만들어 보자 !

(단, lower-case로만 구성된 email address)

(1) 언어에 필요한 모든 Symbol을 정의 한다.

$\sum_{email}$ = { a-z, @, . }

(2) Lemail = $\sum$ . @ . $\sum$ 로 정의하자.

💬 질문: 요 . 는 Concatenation인가 먼가?!

jenny@naver.com $\in$ $\sum^*_{email}$ 인가? ➡️ Yes !

❌BUT❌ 아래와 같은 문제가 있다.

jenny1@naver.com $\in$ $\sum^*_{email}$ ➡️ NO !

a@asdf. $\in$ $\sum^*_{email}$ ➡️ Yes !

a.asdf@asdf $\in$ $\sum^*_{email}$ ➡️ Yes !

@@@@@ $\in$ $\sum^*_{email}$ ➡️ Yes !

(3) Lemail = $\sum_{alpha}$ $\sum_{at}$ $\sum_{alpha}$ $\sum_{dot}$ $\sum_{alpha}$ 로 새롭게 정의하자. (Concatenation)

$\sum_{at}$ = {@}

$\sum_{alpha}$ = {a-z, 0-9, A-Z}

$\sum_{dot}$ = {.}

jenny1@naver.com $\in$ $\sum^*_{email}$ ➡️ OK !

a.asdf@asdf $\in$ $\sum^*_{email}$ ➡️ NO !

@@@@@ $\in$ $\sum^*_{email}$ ➡️ NO !

💬 질문: 이 때 a@asdf. 도 속하는지 ?! 즉 패턴이 저런데 뒤에 시그마 알파가 안와도 되는건지?!

❌BUT❌ 아래와 같은 문제가 여전히 있다.

jenny@any.thing ➡️ OK !

5) 즉, 프로그램 언어에서 토큰을 만들어내기 위해서는 패턴의 규칙을 만들어야 하는데, Sigma Representation 만을 사용해서 Email Address 를 표현하는 Language를 만들기에는 표현력의 한계가 있다.

따라서 더 풍부한 표현력을 가진 '정규 표현식'을 이용해야 한다.

Additional Question

➡️ Does concatenation satisfies commutative property(교환 법칙)?

R1 = {a}, R2 = {b}
R1R2 = {ab}, R2R1 = {ba}
성립하지 않는다.