[PL] Lexical Analysis : Regular Expression

1. 정규 표현식 (Regular Expression)

정규 표현식은 간편하고, 표현력이 좋으며, 정확하고, 널리 사용되고 있다.
토큰들은 일반적으로 정규 표현식을 이용해서 표현된다.

2. 정규 표현식의 Syntax

정규 표현식은 다음 7가지와 같다.

1) 빈 공집합 : $\emptyset$

2) 빈 문자열 : $\epsilon$

3) 시그마 : $\sigma$

4) $R_1$과 $R_2$이 정규표현식일 때, $R_1$ | $R_2$

5) $R_1$과 $R_2$이 정규표현식일 때, $R_1$ . $R_2$

6) R이 정규표현식일 때, ($R$)

7) R이 정규표현식일 때, $R^*$

➡️ Syntax 실습

📌 $\sum$ = {a,b} 일 때, "a.b" 는 유효한 정규표현식 문법인가?

Yes.
규칙(5)에 따라서, "R1.R2"이다.
규칙(3)에 따라서, "a.R2"이다.
규칙(3)에 따라서, "a.b"이다.

📌 $\sum$ = {a,b} 일 때, "a|b" 는 유효한 정규표현식 문법인가?

Yes.
규칙(4)에 따라서, "R1|R2"이다.
규칙(3)에 따라서, "a|R2"이다.
규칙(3)에 따라서, "a|b"이다.

📌"R1 $\cup$ R2"는 유효한 정규표현식 문법인가?

NO.
$R_1$ | $R_2$ 는 정규 표현식이지만, $R_1$ $\cup$ $R_2$ 는 정규 표현식이 아니다. 이것은 Set Operation 이기 때문에, 옳지 않다.

📌$\sum$ = {a,b,c} 일 때, "a*.b|c"는 유효한 정규표현식 문법인가?

YES.

3. Regular Language

1) Regular Language란, 정규 표현식을 사용하여 나타낸 언어를 의미한다.

정규 표현식은 언어를 정의하는데, 언어는 '정규 표현식이 표현할 수 있는 모든 문자열의 집합'이다.

2) 정규표현식 R의 언어 L(R)은 다음과 같다.

(1) L($\emptyset$) = $\emptyset$

$\emptyset$ 을 이용하여 표현 가능한 모든 문자열은 $\emptyset$ 이다.

(2) L($\epsilon$) = {$\epsilon$}

$\epsilon$ 을 이용하여 표현 가능한 모든 문자열은 $\epsilon$ 이다.

(3) L($\sigma$) = {a}, where $\sigma$ is a

$\sigma$ = a 일 때, $\sigma$ 로 표현 가능한 모든 문자열은 a이다.

(4) L($R_1$ | $R_2$) = {L($R_1$) $\cup$ L($R_2$)}

$R_1$ 합집합 $R_2$ 을 이용하여 표현 가능한 모든 문자열은 L($R_1$) $\cup$ L($R_2$) 이다.

(5) L($R_1$ . $R_2$) = {L($R_1$) . L($R_2$)}

$R_1$ 접합 $R_2$ 을 이용하여 표현 가능한 모든 문자열은 {L($R_1$) . L($R_2$)} 이다.
✔️참고: 두 문자열 집합 A와 B에 대하여, A.B = {xy| x $\in$ A and y $\in$ B } 이다.

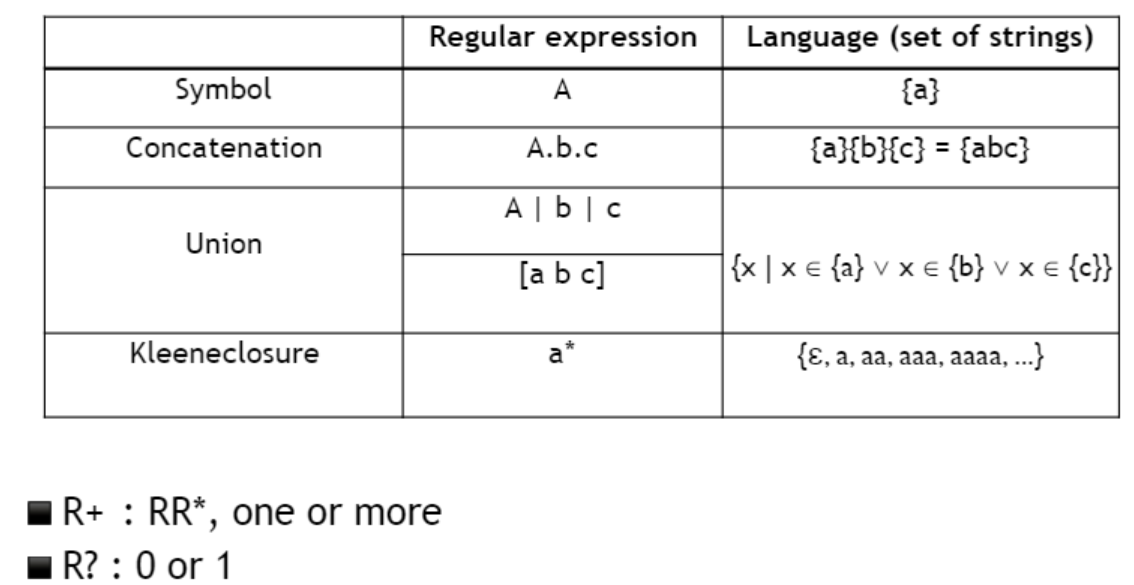
🌳주의사항

• Union은 [a b c] 와 같은 형식으로도 표현할 수 있다.
• Kleene Closure R+ 은 하나 이상으로, RR*과 같은 의미를 가진다.
• R?은 0 혹은 1을 의미한다.

➡️ 실습

📌 L($R_1$ | $R_2$) = L($R_1$) $\cup$ L($R_2$) 로, 하위 내용이 성립한다.

✔️ L(a|b) = L(a) $\cup$ L(b) = {a} $\cup$ {b} = {a,b}
✔️ L(a|b|c) = L(a|b) $\cup$ L(b) = {a, b} $\cup$ {c} = {a, b, c}
✔️ L(a|$\epsilon$) = L(a) $\cup$ L($\epsilon$) = {a} $\cup$ {$\epsilon$} = {a, $\epsilon$}
✔️ L($\epsilon$|$\epsilon$) = {$\epsilon$}
💬 왜 {$\epsilon$, $\epsilon$} 이 아님?!
✔️ {$\epsilon$} != {}
전자는 원소가 하나인 집합이고, 후자는 공집합이다.
✔️ a$\epsilon$ == a 인가?!
Yes. $\epsilon$는 빈 문자열이기 때문에 제거 가능하다. a$\epsilon$ = $\epsilon$a = a이다.

📌 L($R_1$ . $R_2$) = L($R_1$) . L($R_2$) 로, 하위 내용이 성립한다.

✔️ L(a.b)로 생성 가능한 문자열?!
L(a.b) = L(a).L(b) = {a}.{b} = ab

✔️ L((a|b).c) 로 생성 가능한 문자열?!
L((a|b).c) = L(a|b).L(c) = (L(a)$\cup$L(b)).L(c) = ({a}$\cup$ {b}).L(c) = {a,b}.{c} = {ac, bc}

✔️ L(a|b*) 으로 만들어낼 수 있는 string은 무엇이 있는가?
L(a)UL(b*) = {a}U{$\epsilon$, b, bb, bbb ... } = {a, $\epsilon$, b, bb, bbb...}

✔️ L((a|b)*) 으로 만들어낼 수 있는 string은 무엇이 있는가?
L((a|b)*) = L({a,b}*) = {$\epsilon$, a, b, aa, ab, ba, bb, aaa, aab, aba, abb, baa, bab, bba, bbb ... }

✔️ L(a.b*)으로 만들어낼 수 있는 string은 무엇이 있는가?
L(a.b*) = L(a).L(b*) = {a}.{$\epsilon$, b, bb, bbb.. } = {a, ab, abb, abbb ... }

✔️ A = {aa, b} B = {a, b} 일 때 L(A.B) = L(A).L(B) = {aa,b}.{a,b} = {aaa, aab, ba, bb}
💬 ab도 L(A.B)에 속하나?! 안 속할듯

✔️ A = {aa, b, $\epsilon$}, B = {a, b} 일 때 L(A.B) = {?!}
💬 답 = L(A.B) = L(A).L(B) = {aa, b, $\epsilon$}.{a, b} = {aaa, aab, ba, bb, $\epsilon$a, $\epsilon$b} = {aaa, aab, ba, bb, a, b} 맞나 ?!

4. 정규표현식의 Operation Precedence

* > . > |

✔️ L(a|b.c)는 a|(b.c) 를 의미한다.

✔️ L(a|b.c) = L(a|L(b).L(c)) = L(a|{b}.{c})
= L(a|{bc}) = L(a) $\cup$ {bc} = {a, bc}

✔️ L(a.b|c) = L(ab | c)

5. 정규표현식의 Parentheses

정규표현식에서 괄호를 사용할 수 있다.

✔️ L((R)) = L(R)

✔️ L((a|b).c) = L(a|b).L(c) = {a,b}.{c} = {ac, bc} 처럼 괄호가 . 보다 높은 우선 순위를 가진다.

✔️ 괄호를 'symbols'로서 사용하고 싶으면 escape sequence를 사용하여 \(, \) 로 사용할 수 있다.

6. 정규표현식의 Kleene Star

> zero or more

L($R^*$) = {$\epsilon$} $\cup$ L($R$) $\cup$ L($R$).L($R$) $\cup$ L($R$).L($R$).L($R$) $\cup$ L($R$).L($R$).L($R$).L($R$) $\cup$ ...

$L^0$($R$) = {$\epsilon$}
$L^i$($R$) = $L^{i-1}$($R$).$L$($R$)
$L^*$($R$) = $U_{i>=0}$$L^i$($R$)

➡️ 실습

📌 $R^*$ = a = {$\epsilon$, a, aa, aaa, aaaa .. } = zero or more

📌 $R$$R^*$ = aa* = {a, aa, aaa .. } = one or more

📌 정규 표현식에서 one or more을 지칭하기위해 "+" 을 사용하기도 한다.

💬$R^*$ = a 인데 $R$$R^*$ = aa* 인게 맞나?

➡️ 실습 : 정규 표현식으로 휴대폰 만들기

LphoneN = "010-7777-7777" 와 같이, 휴대폰 번호를 나타내는 언어 만들기.

(단, 010- 으로 시작한다고 가정)

📌 1) [0-9]+-[0-9]+-[0-9]+

But "12-1-1" 같은 경우도 포함된다.

📌 2) [0-9][0-9][0-9]-[0-9][0-9][0-9][0-9]-[0-9][0-9][0-9][0-9]

But "111-1111-1111"도 포함

📌 3) 010-[0-9][0-9][0-9][0-9]-[0-9][0-9][0-9][0-9]

➡️ 참고

📌 a | b 를 a + b 로 만들 수 있을까? regular expression a | b를 regular expression equation x = a + b 로 바꿀 수 있다.

regular expression => regular expression equation
x -> a | b => x = a + b
y -> c | d => y = c + d
z -> e | f => z = e + f

📌 Can a string, created out of a union be longer than two digits?

R1 = {a} R2 = {b}
R1 U R2 = {a, b}

=> 불가능하다. 2digit인 aa, ab, ba, bb 는 Union으로 만들 수 없기 때문 !

📌 이론적으로 regular exrpession은 recursive하게 정의될 수 없다. 따라서 아래와 같은 정규표현식은 invalid하다

program = statement*
statement = statement PLUS statement | NUM | parenthesis
parenthesis = (statement)