
🔔 TFAE 정의
TFAE를 정의해 보자.

expr + expr,expr - expr
ʎ.x : t.expr
함수 정의이다. expression에 대해서 type을 부여하고 있다.
expr expr
함수 application이다.
t::= num | bool | t -> t
type에는 number(int), boolean, arrow type(함수 타입) 으로, 3가지 타입이 있다.
🌳 Type Rules
타입 규칙들을 정의하여, evaluate과정 전에 잘못된 expression들을 감지할 수 있도록 할 것이다!
type system = type rule의 집합

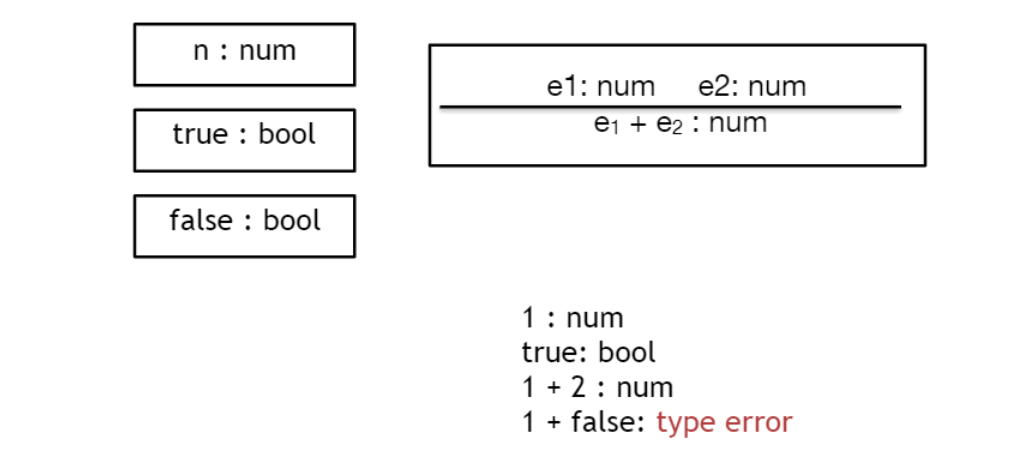
1은 num이고, true는 bool이다.
1+2는 무슨 타입일까?
+ 연산자는 num과 num을 받아서 num을 반환해야 한다.

+는 num 2개를 기대하고 있는데 false는 boolean이므로, type error이다.
🌳 type rule 만들기
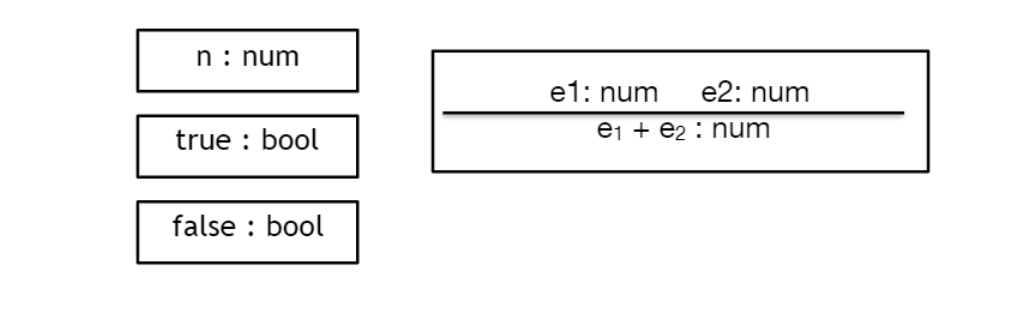
e1이 num이고 e2가 num이어야 e1 + e2 : num type이다.
위 룰을 통해 위와 같이 검증할 수 있다

위 같은 경우는 어떻게 type checking을 할 수 있을까?
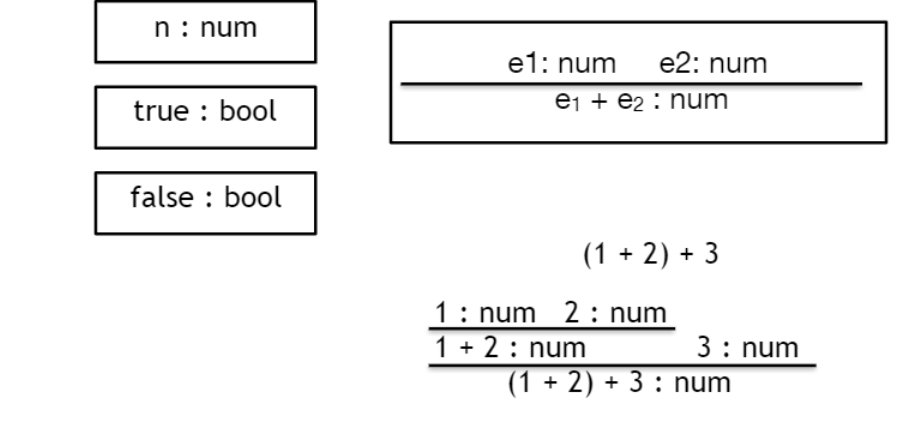
위와 같이 할 수 있다.
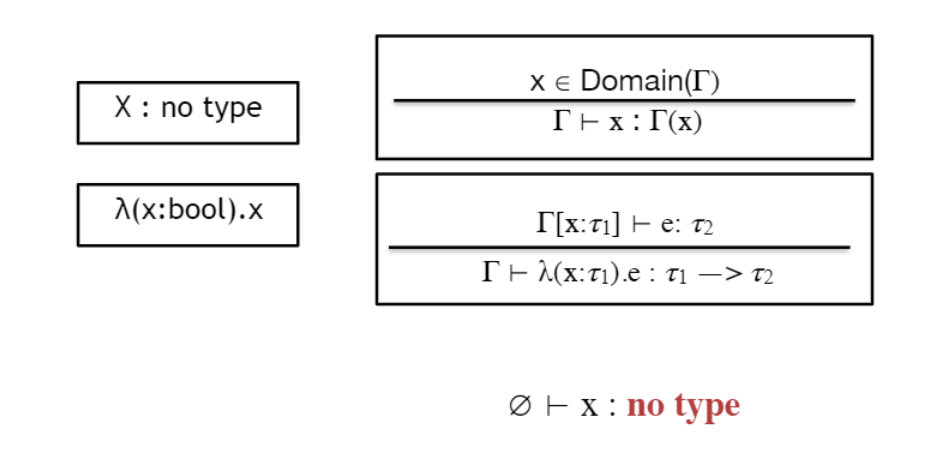
x를 아직 정의하지 않은 상태라면 x는 free identifier이다. 그 타입을 알지 못한다.
ʎ(x:bool).x 는 함수이다.
x는 파라미터이며, 그 파라미터의 type은 bool이다. 함수 바디는 x이다.
x가 bool이기 때문에, 이 함수는 bool을 인자로 받고 bool을 리턴한다.

x가 type environment Γ에 정의되어 있다면,
그 하에서 x는 Γ(x)이다.
함수에서 x:t1이라면 environment를 Γ[x:t1] 로 업데이트 시킨다.
만약 environment Γ[x:t1] 에서, 함수 바디 e의 type이 t2라면,
Γ에서, ʎ(x:t1).e 의 type은 t1 -> t2이다.
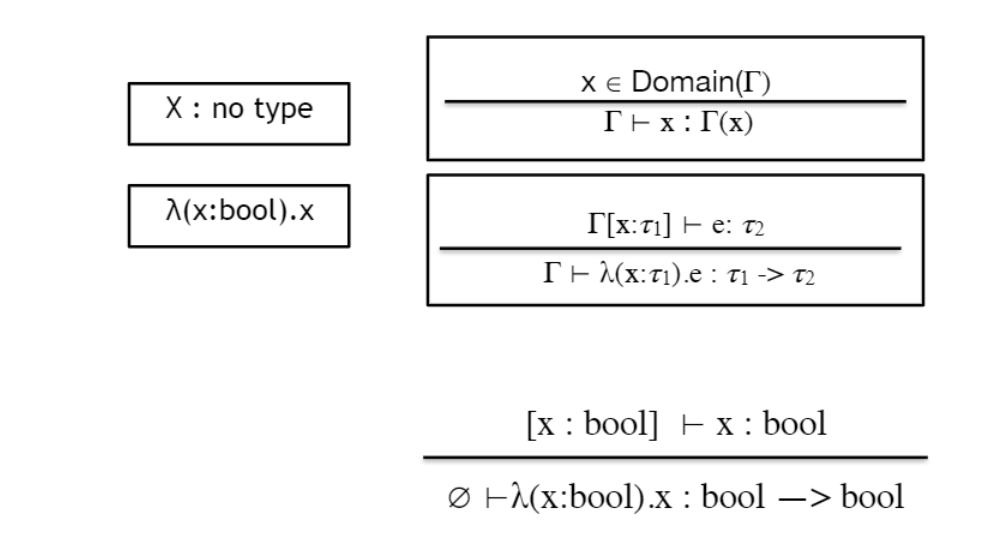
따라서 ʎ(x:bool).x는 위와 같다.
🌳 Revise Type Rules
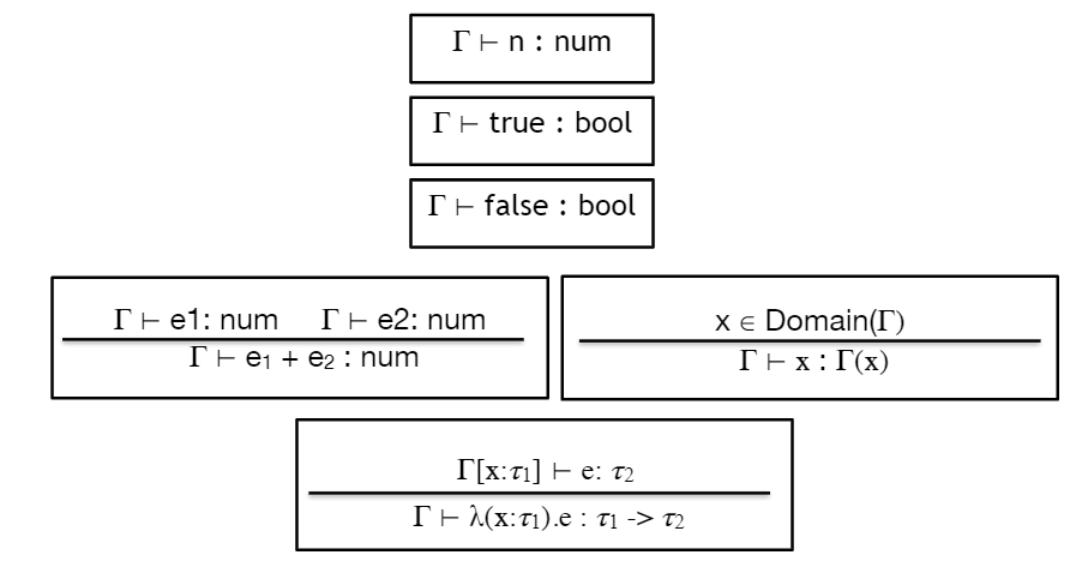
기존에 정의한 타입들에 type environment Γ를 모두 추가해 주자!

Function Call에 대한 type은 없는 상태이므로, 정의해 보자!
함수 호출e1(e2)에 대해서,
e1은 함수 타입이어야 한다.
따라서, e1의 타입이 t1 -> t2이고, e2의 타입이 t1라면, e1(e2)은 t1 -> t2 타입이다.
Example
7(5)의 경우, 7은 함수 타입이 아니므로 타입 에러가 발생한다.
-> 현재 e1(e2) 형태는 파라미터가 1개뿐이다.
따라서 multiple parameter가 가능하도록 확장해 보자!
🌳 Multiple Parameter로 확장

🌱 함수 정의
함수 ʎ 에서 multiple parameter x1, .. xn에 대해 각각 type을 지정해 준다.
그리고 type environment를 update하여, Γ[x1:t1,.. xn:tn]이 된다.
Γ[x1:t1,.. xn:tn] 환경에서 e의 타입이 t0일 때,
Γ(x1:t1,.. xn:tn).e는 (t1..tn) -> t0 타입이다.
🌱 함수 application
함수 e0이 (t1, .. t2) -> t0 타입인 환경에서, 그리고 e1은 t1이고, e2는 t2타입이고, .. en은 tn 타입인 환경에서 (각 파라미터 타입)
e0(e1, .. en)의 타입은 t0이다.
