
조건문이 가능하도록 TFAE를 확장해보자.

🌱 if expr expr expr은 조건문을 나타낸다.
Question #1: What is the type of the following expression? λx.x + 1
이것은 엄격히 말하면 옳은 expression이 아니다.
우리의 문법상
λ.x:t.expr로, argument type이 명시되어야 하는데 명시하지 않았기 때문이다.그래도 이 expression의 type을 추론할 수 있다.
x가 파라미터, x+1이 함수의 바디라는 것을 추론할 수 있다. 파라미터 하나를 받아서 1을 더하여 리턴한다.
+는 num과 num에서만 가능하므로, x는 num 타입일 것이다.따라서, 이 expression은
int -> inttype임을 추론할 수 있다.
🌳 Type Inference
Type Inference란 프로그래머가 생략했을 때, type annotation을 삽입하는 것이다.
우리는 explicit question mark를 사용하여, 어떤 부분에서 type이 생략되었는지 명시해보자.
λx.x + 1로 쓸 수도 있지만, λx.?x + 1 로 작성해 보자.
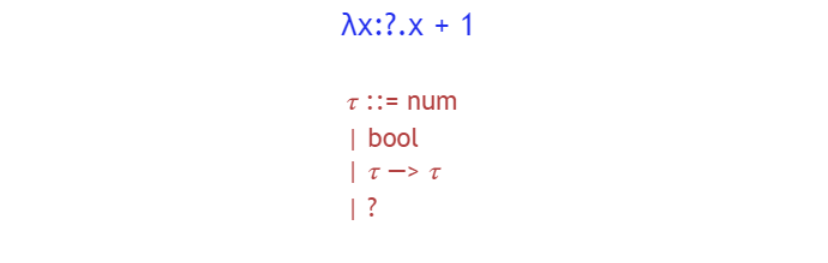
타입 추론 과정은 아래와 같이 이뤄진다.

🔔 Example

if expr expr expr에서 if 조건문 첫 브랜치 두번쨰 브랜치인데, 두브랜치는 type이 동일해야 한다.
첫 브랜치가 num이므로 두 번째 브랜치도 num이어야 한다. 따라서 t1 = num이다.
🔔 Example

if x 1 x에서, 첫 번쨰 x는 조건문으로서 condition이기 때문에 bool type이어야 한다
그런데 두번째 x는 else statement로서 1과 동일한 타입이어야 하므로 num type이어야한다.
x는 bool이면서 동시에 num일수는 없으므로, if x 1 x 는 no type이다. -> type error!
🔔 Example
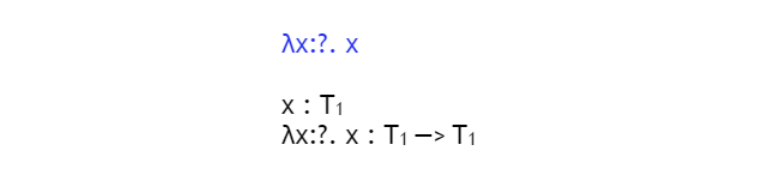
이 expression의 type은 t1 -> t1이다.
여러 케이스가 모두 가능하다.
num -> num일수도, bool -> bool일수도, (num->bool) -> (num->bool) 일 수도 있다.
따라서 타입 체커는 variable들을 reported type으로 남겨둬야 한다.
🔔 Example

function call expression이다
🔔 Example
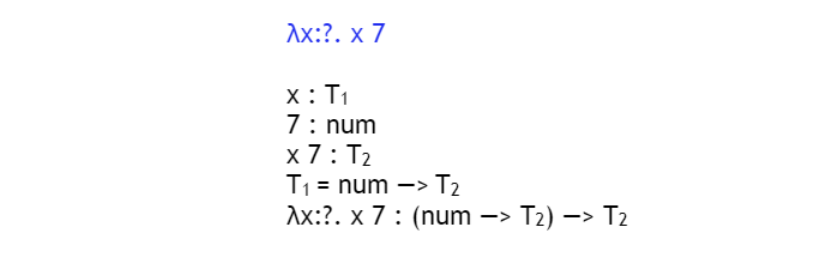
x 7는 function이다. x 7 를 t2 type이라고 해 보자.
x가 t1이라면,
t1 : num -> t2이다.
따라서 전체 표현식은 (num->t2) -> t2가 된다.
🔔 Example

x x는 function call expression이다.
x는 t1 type이라고 가정하고, t1은 t2->t3이라고 생각해 보자.
-> 계속되는 cycle이 만들어진다. = "Cylic Calls"
즉, 결국 x의 type을 알 수는 없다.
