🌳 Symbolic Execution (기호실행)
기호실행이란, 소프트웨어 테스팅 기술이다.
symbolic 변수를 사용해서, 프로그램 input을 symbolic 변수로 교체하는 것이다.
Dynamic 기호실행이란
프로그램 input을 symbolic 변수로 교체하는 것에 넘어, 실제로 프로그램을 실행해 보는 것이다.
Dynamic 기호실행의 두가지 종류
🌳 Concolic Testing (Concrete + Symbolic)
Concolic 테스팅은 3가지 정보를 유지한다.
1) concrete state 정보
프로그램의 실제 값을 저장하는 state이다.
input = (22, 7)이라면 concrete state = 22, 7이다.2) symbolic state 정보
프로그램 변수를 symbolic 변수로 대체한 것이다.
symbolic 변수 a, b로서 x => a, y => b로 표현한다.3) path condition 정보
condition 문을 만날 때마다 업데이트된다.
🌳 Concolic Testing 동작 방식
1) 1st iteration

(1) x = 22, y = 7 입력을 넣는다.
z = 14로, concolic state는 update 된다.
(2) symbolic state update
(3) 조건문 만나지 않았으니, PC = True(초기값)

(1) z == x 문에서 해당하지 않으므로 마지막 코드로 이동한다.
(2) z != x 를 업데이트 해야 한다.
따라서 Path Condition에 symbolic 변수로 변환되어 2b != a로 쌓이게 된다.
🔔 SMT SOLVER
if 문을 통과시키기 위해, Path Condition을 뒤집어서 2b = a 인 input을 만들어내게 한다.
a = 2, b = 1의 테스트 케이스를 새로 생성한다.
2) 2nd iteration

(1) x = 2, y = 1 입력을 넣는다.
z = 2로, concolic state는 update 된다.
(2) symbolic state update
(3) 조건문 만나지 않았으니, PC = True(초기값)

(1) z == x이므로, if문 안으로 들어간다.
(2) path condition에 2 * b = a 가 쌓이게 된다.
(3) x > y+10이 아니므로, 마지막 코드로 이동한다.
(4) path condition = (2 * b = a) ∩ (a <= b + 10)이 쌓이게 된다.
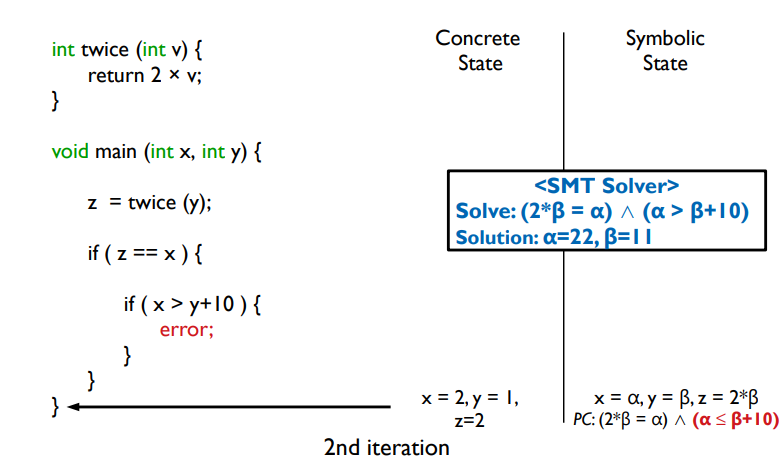
🔔 SMT SOLVER
If문을 통과하지 못한 해당 조건을 뒤집는다.
SMT Solver에게 (2 * b = a) ∩ (a > b + 10) 를 주면, 이를 만족하는 입력을 만들어 낸다. 결과적으로 a = 22, b = 11인 테스트 케이스를 생성한다.
3) 3rd Iteration


내부 if문까지 통과하여, error 지점까지 도달할 수 있게 된다!
🌱 Concolic Testing의 핵심 아이디어
concrete state, symbolic state, path condition 정보를 유지하면서 프로그램이 끝날 때마다 SMT Solver에 방정식을 주고, 방정식을 만족하는 해를 받아서 다음에 필요한 테스트케이스를 생성한다.
🌳 Non-linear Constraint : SMT Solver의 한계
값을 두배 해주는 twice 함수를, 값을 '제곱'하는 함수로 바꿔보자.
1) 1st iteration

(1) x = 22, y = 7 입력을 넣는다.
z = 49로, concolic state는 update 된다.
(2) symbolic state update
(3) 조건문 만나지 않았으니, PC = True(초기값)

(1) z == x 문에서 해당하지 않으므로 마지막 코드로 이동한다.
(2) z != x 를 업데이트 해야 한다.
따라서 Path Condition에 symbolic 변수로 변환되어 b * b != a로 쌓이게 된다.

SMT Solver에게
b * b = a방정식을 전달한다.
그러나 SMT Solver가 linear 방정식은 잘 해결하지만 non linear 의 경우는 잘 해결하지 못한다.
따라서 이렇게 풀기 어려운 방정식의 경우에는, condition을 특정 concrete 값으로 바꾸어서 해를 구하기 쉽도록 한다.
예를 들어, b = 7로 바꾸어서7 * 7 = 49로 해 (49, 7)를 찾을 수 있게 했다.
2nd iteration

(1) 첫 번째 그림
Symbolic state 빈칸 : 모두 b * b
path condition 빈칸 : 전자 b * b = a / 후자(b * b = a ) ( a >= b +10)
(2) 두번째 그림
두번째 if문을 통과하지 못한다.
path condition = (b * b = a ) ( a >= b +10)이 쌓이게 된다.
🔔 SMT Solver가 풀어야 할 것
(b * b = a ) ( a < b +10)
역시 nonlinear하기에, concrete 값으로 바꾸어보면 49 == a, a < 17이 된다. -> 불가능
이러한 경우 SMT Solver가 concrete 값으로 교체하더라도, 에러 지점에 도달하는 입력을 만들어내지 못한다. 이것이 SMT Solver의 한계이다.
🌳 external function
실제 코드에서는 함수의 바디가 없는 외부 함수들을 호출하는 경우가 많다.
이런 경우 어떻게 할까?
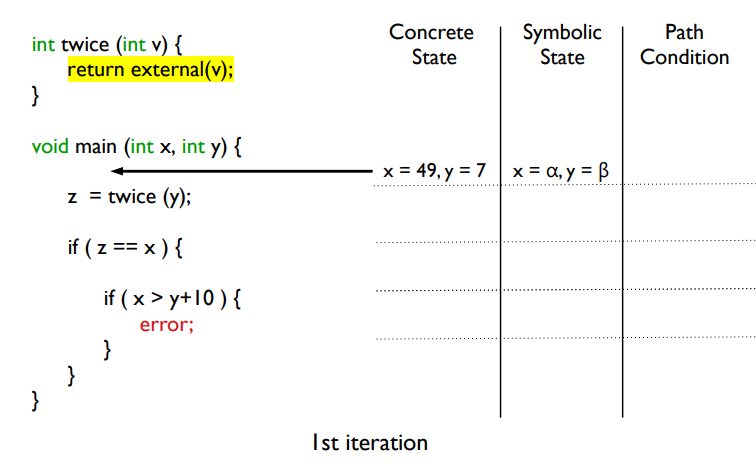
external 함수를 hash 함수로서, 매우 큰 값을 반환하는 함수라고 생각해 보자.
(1) concrete state : x = 49, y = 7
symbolic state : x = a, y = b
path condition : true
(2) concrete state : x = 49, y = 7, z = 3712345
symbolic state : x = a, y = b, z = hash(b)
path condition : true
(3) 첫 if문을 만난다.
concrete state : x = 49, y = 7, z = 3712345
symbolic state : x = a, y = b, z = hash(b)
path condition : hash(b) != a
프로그램 종료된다.
SMT Solver의 입력은 hash(b)==a 이 된다.
b가 7일때 리턴되는 값을 알고 있으므로, hash(b) = 3712345이므로, a = 3712345이다.
따라서 다음 x = 3712345, b = 7 이 된다.-> 이처럼 외부함수의 바디를 알지 못하더라도, 실제 실행하여 알아낸 값으로 다음의 테스트케이스 입력값을 만들어낼 수 있다는 장점이 있다.