
🌳 SMT(Satisfiability Modulo Theories) Solver의 동작 방식
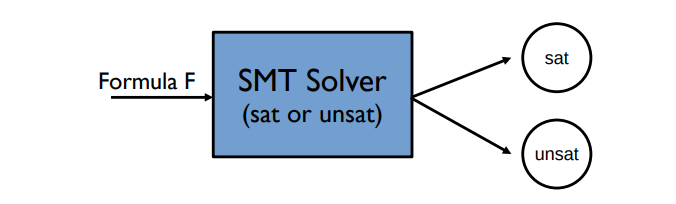
formula F를 입력받고, F가 Satisfiable한지 아닌지를 체크하는 역할을 한다.
ex) F가 boolean formula라고 할 때,
p와 q의 값이 F를 참으로 만드는 p와 q의 값이 존재한다면 F가 Satisfiable 하다
어떠한 p, q로도 F를 참으로 만들 수 없을 경우 Unsatisfiable하다.
ex 1. 위 formula는 satisfiable한가?

satisfiable 하다! p, q = (F, F)인 경우 위 Formula는 satisfiable하다.
ex 2. 위 formula는 satisfiable한가?
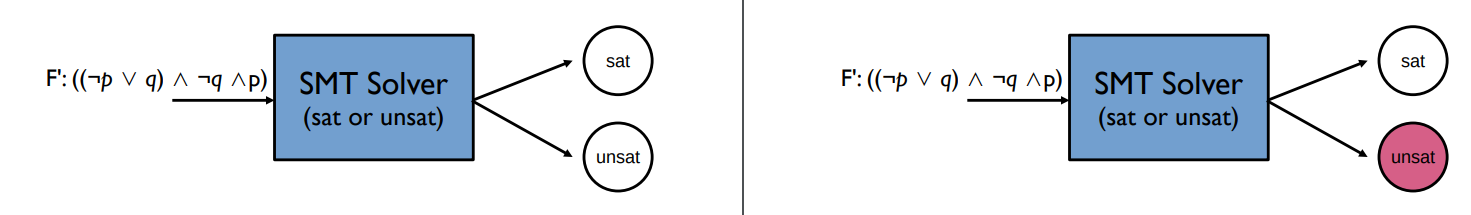
위 경우 만족시키는 p, q의 조합은 없기 때문에 Unsatisfiable하다.
ex 3. 위 formula는 satisfiable한가?
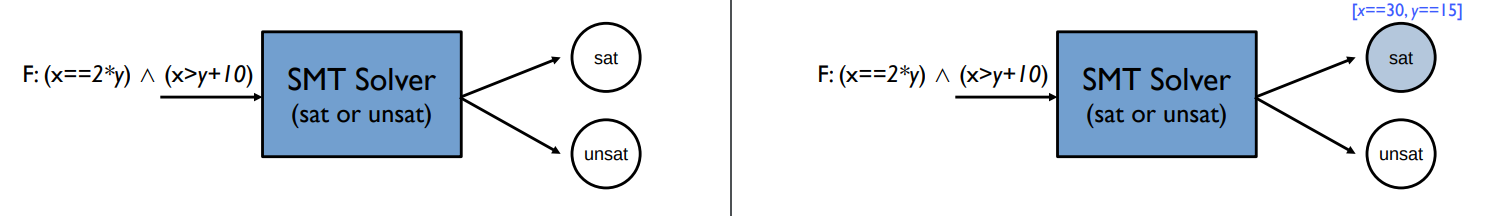
satisfiable 하다! 위 방정식을 풀어 보면 가능한 것을 알 수 있다.
📌 현실적인 문제
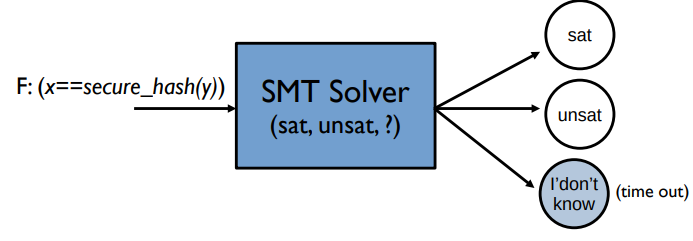
그러나 현실에서 모든 방정식을 풀 수 있는 SMT Solver는 존재하지 않는다.
따라서 특정 시간 내에 판단하기 어려우면, 'i don't know'라고 리포트한다.따라서 path condition을 잘 준다고 하더라도, SMT Solver가 이를 풀지 못한다면 input을 만들 수 없기 때문에 SMT solver가 concolic testing의 중요한 부분이다.
🌳 Concolic Testing의 동작 방식
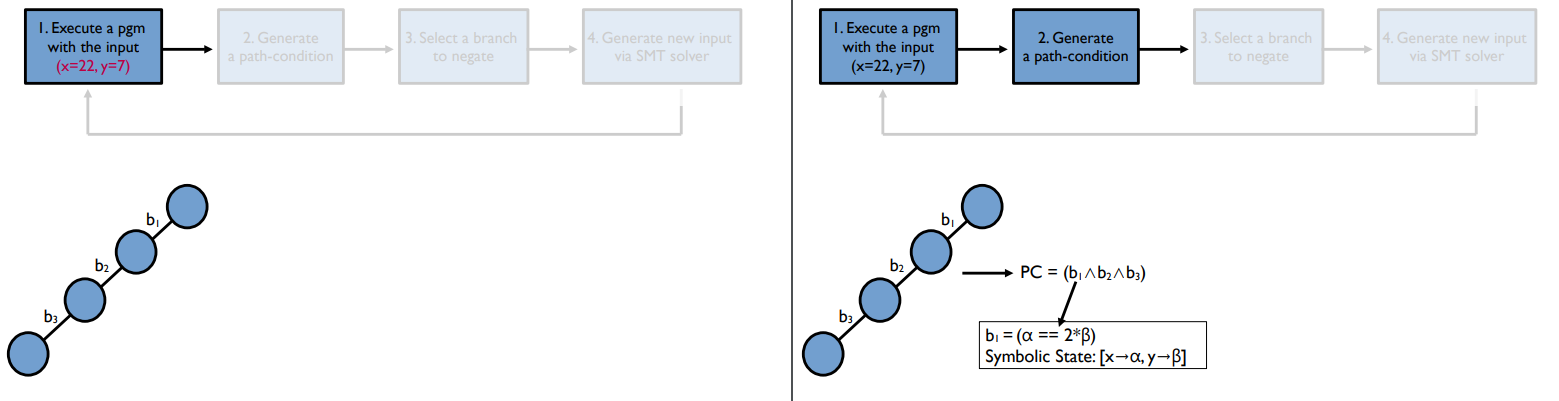
1) program을 특정 input으로 실행시킨다.
2) path condition을 generate한다.
각 브랜치가 3개 있고, 그 3개의 조건문에 대해 path conditon이 위와 같이 쌓이게 된다.
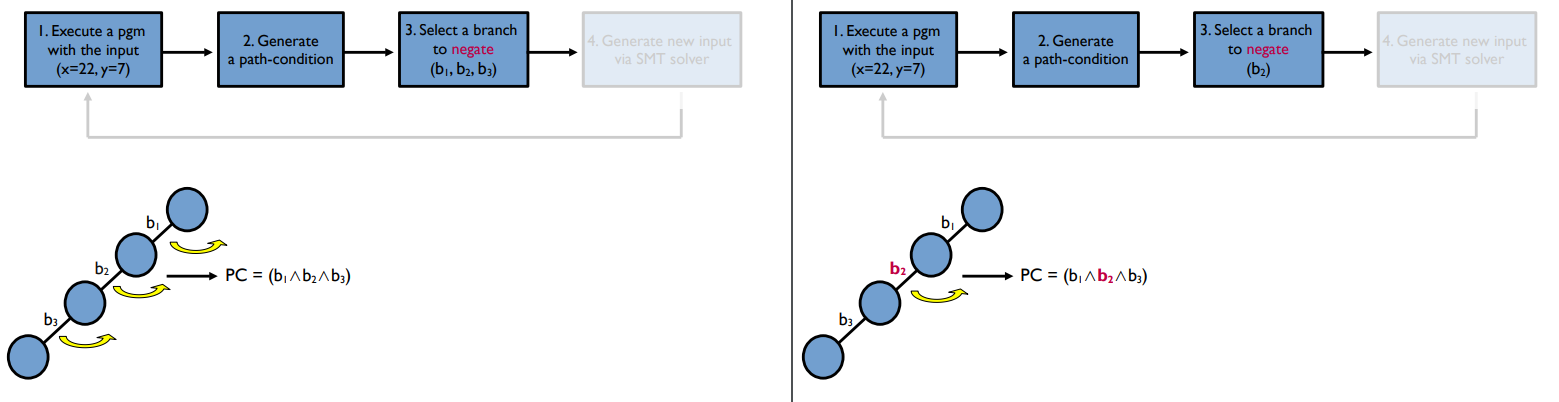
3) 뒤집을 path condition(branch)를 선택한다.
b2와 반대되는 path를 가보고 싶다면, b2를 뒤집으면 된다.
4) SMT Solver를 통해 새로운 인풋을 만든다.
SMT Solver의 input으로 b1은 참이면서, b2는 negate한 condition을 준다. SMT Solver는 new input (22, 11)을 generate한다.
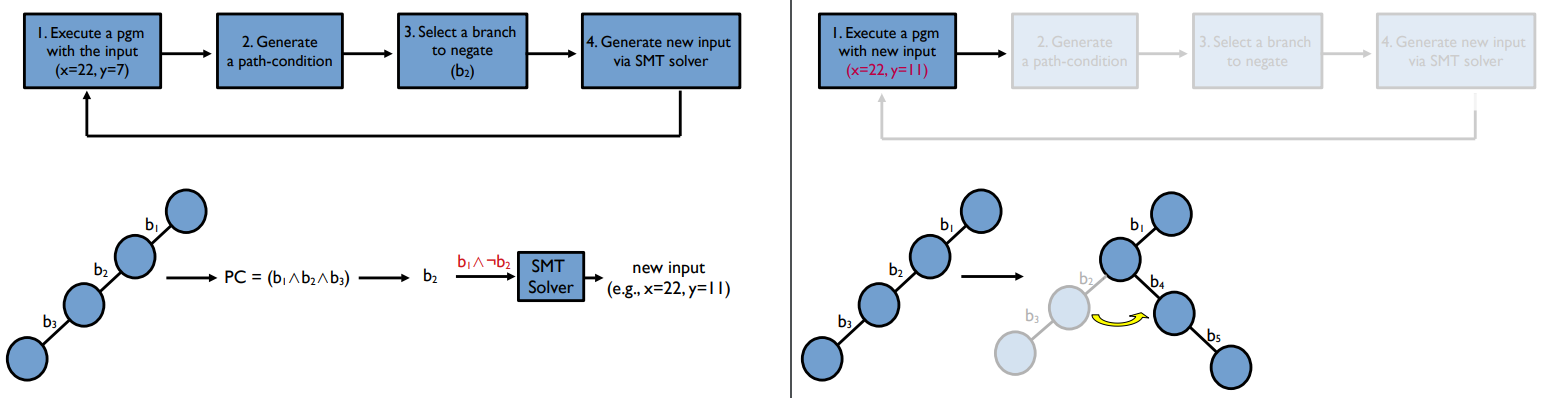
반복 1) program을 새 input으로 실행시킨다.
뒤집은 condition에 대해 다른 branch를 갈 수 있게 된다.
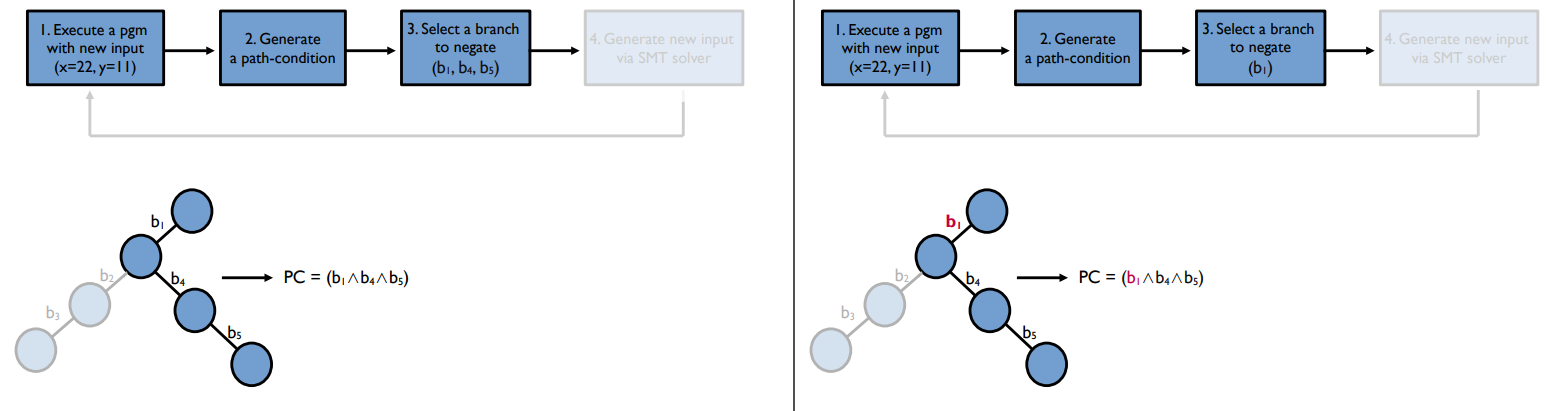
2) path condition을 generate한다.
이 경우 b1, b4, b5의 branch가 path condition으로 쌓이게 된다.
3) 뒤집을 path condition(branch)를 선택한다.
b1과 반대되는 path를 가보고 싶다면 b1을 뒤집는다.
4) SMT Solver를 통해 새로운 인풋을 만든다.
SMT Solver의 input으로 b1을 negate한 condition을 주고, new input을 generate한다.

🌳 Concolic Testing Algorithm
Input = 프로그램 p, 초기값 v, 실행 횟수(budget) n
1: 초기 입력을 v로 준다.
2: for문으로 총 실행 횟수만큼 루프를 돈다.
3: 값 v로 프로그램을 돌려서 실행한 후, path condition Ø 을 생성하게 된다.
5: 그 path condition Ø 중 뒤집을 condition 하나를 고른다.(Choose)
6: condition이 c1, c2, c3가 있다고 할 때 c2를 뒤집으면 path condition = c1 ∩ ~c2 가 된다. (c3는 그대로 둔다)
즉, ci를 고르면 i보다 작은 j는 모두 ∩ 조건으로 묶고, 마지막 ci만 뒤집는다.
이 때 이 조건이 satisfiable한 조건인지 체크해야 한다❗❗ 만약 unsatisfiable하면 테스트케이스를 만들어내지 못하기 때문이다.
7: satisfiable 하다면, 테스트케이스를 generate한다. 루프를 돌게 된다.
