1. 비모수 통계

1. 비모수통계(Non-parametric Statistics)

• 표본 데이터의 일정한 특징에 대한 가정이 위배되는 경우에 사용
• 소규모 표본일 경우 ('표본이 모집단을 대표하기 충분히 크다라는 가정이 위배되는 경우)에 사용
• 모수에 대한 가정이나 추정을 전제로 하지 않음
  • 모집단의 형태에 관계없이 주어진 자료에서 직접 확률을 계산하여 통계적 검증을 하는 분석 방법
  • 분포에 구애받지 않는 분포 자유 검증이라고도 알려짐
• 모집단의 모수에 대한 추론이 아닌 빈도, 비율, 기호, 순위와 같은 질적인 자료를 다루는 통계 분석 방법
• 모집단 모수에 대한 아무런 가정을 하지 않음

2. 모수 vs 비모수 검정

• 모수적 검정
  • 모집단의 분포에 대해 가정하고 검정을 수행
  • 특정 표본에에서 얻은 통계량을 통해 모집단의 특성을 유추
  • 예. t검정, 대응표본 t검정, ANOVA 등
• 비모수 검정
  • 모집단의 분포를 가정하지 않고 검정을 수행
  • 모수 검정의 조건이 만족되지 않거나 표본의 크기가 작을 경우 사용
  • 표본의 중심 위치로 평균 대신 중양값 사용

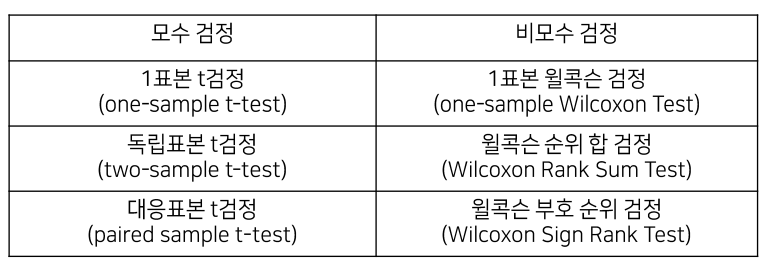
2-1. 모집단 1개 (표본 1개)

• 모수적 검정 : 단일표본 t-검정 (모집단의 분산을 알면 z-test)
• 비모수검정 : 부호(sign) 검정,월콕슨(WiIcoxon) 검정

2-2. 모집단 2개 (표본 2개)

• 모수적 검정 : 독립표본t-검정 (two-sample t-test)
• 비모수 검정 : 월콕슨 순위 합 검정(Wilcoxon Rank Sum Test),
  맨휘트니 U검정 (Mann-Whitney IJTest)

2-3. 모집단 전/후 동일 개체 (대응 표본)

• 모수적 검정 . 대응표본t-검정 (paired t-test)
• 비모수 검정 : 월콕슨부호 순위 검정(WiIcoxon Sign Rank Test)

2-4. 모집단 3개 이상 & 요인 1개 (표본 3개 이상 &요인 1개)

• 모수적 검정 . 일원분산분석(one-way ANOVA)
• 비모수 검정 : 크루스칼왈리스 검정(Kruskal-Wallis Test)

2-5. 모집단 3개 이상 & 요인 2개 (표본 3개 이상 & 요인 2개)

• 모수적 검정 : 이원분산분석(two-way ANOVA)
• 비모수 검정 : 프리드먼 검정(Friedman Test)

2-6. 범주형 데이터 분석: 2ⅹ2

• 모수적 검정 : 카이제곱검정(Chi-square Test)
• 비모수 검정 : 피서의 정확도 검정(Fisher's Exact Test)

3. 월콕슨 검정

• 월콕슨 검정(Wilcoxon Test) : 표본의 정규성이 확보되지 않을 때
  두 집단의 사이를 비교할 경우 t검정 대신 사용하는 비모수 검정 방
  법 중 하나
  

• t-test : 두 집단 비교시 평균, 표준오자에 따라 분석

  • 정규성 가정 필요

• 월콕슨검정 : 너무 작은 표본수의 평균을 비교하면 소수의 극단치에 의해 평균이 크게 영향을 받음

  • t검정 수행 시 유의하다는 결론 유도
  • 두 개의 자료를 '순위(rank)'에 따라 새로운 자료를 만들어 이용
  • 극단치의 영향을 줄일 수 있음.

• 두 집단의크기에따른부호(sign)에서 순위(rank)를고러

• signed rank:

1. 두 값을 비교(차이)하여 부호(sign)을 만든다.이때 부호는 3가지 경
   우 (증가(+), 감소(-), 동일) 중 하나를 가짐.
2. 이 값들의 크기(절대값)에 따라 순위(rank)를 정해준다. 절대값이 증가함에 따라 순위도 증가.

4. R을 이용한 Wilcoxon Test

다음 자료는 갑과 을, 두 지역에신호등을 설치할 것인가를알아보기 위해
10일간 일정한 시간 동안 통과하는 차량 수를 조사한 것이다. 지역에 따라
통과 차량의 수가 다른지를 검정하라

• 관련 함수: wilcox.test(x~factor, data=data 이름, correct=FALSE,
  exact=FALSE, paired=T)
• Ⅹ: 정량적인 수치
• factor: 요인변수
• data : data 이름
• correct, exact : 입력 data에 동일 순위가 있을 경우 계산을 위해
  FALSE로 명시적으로 입력
• paired : defaut는 FALSE

# 지역별 통행량 data 입력
countA <- c(592,625,777,613,587,637,629,843,544,668)
countB <- c(622,644,664,853,608,635,885,668,649,714)
countAll <- c(countA,countB)
# 지역 label 만들기
region <-c(rep('regionA',10),rep('regionB',10))
# 지역별 통행량을 data frame으로 전환
sampleData <- data.frame(region,countAll)
sampleData

# 지역별 평균값 구하기
tapply(sampleData$countAll, sampleData$region, mean)
regionA regionB
651.5 694.2
# 지역별 표준편차 구하기
tapply(sampleData$countAll, sampleData$region, sd)
regionA region
91.19728 96.79509

# 지역별 통행량 boxplot
boxplot(countA,countB, main ='지역별 통행량', xlab='지역',ylab='통행량')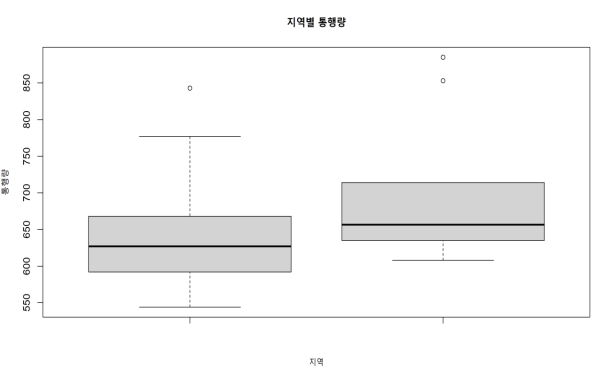

# Wilcoxon 순위 합 검정
wilcox.test(countAll~region, data=sampleData, correct = FALSE, exact=FALSE,
paired=FALSE)
Wilcoxon rank sum test
data: countAll by region
W = 30.5, p-value = 0.1403
alternative hypothesis: true location shift is not equal to 0

5. R을 이용한 Kruskal-Wallis Test

• 세 개 이상의 집단을 비교하기 위한 방법

다음 자료는 4 종류 복사기에 대한 평균 고장 시간을 측정한 자료이다.
4 종류 복사기에 대한 평균 고장 시간에 사이가 있는지 검정하라.

• 관련 함수: KruskaI.test(x~factor, data=data이름)
• Ⅹ: 정량적인 수치
• factor: 요인변수
• data : data 이름

# 고장시간 입력
failureTimeA <- c(28,41,34,52,25)
failureTimeB <- c(5,16,20,24,15)
failureTimeC <- c(10,8,18,14,26)
failureTimeD <- c(45,30,49,32,36)
failureTimeAll<- c(failureTimeA,failureTimeB,failureTimeC,failureTimeD)
# 기기 별 label 만들기
machine <- c(rep('A',5),rep('B',5),rep('C',5),rep('D',5))
# data frame 형태로 변환
sampleData<- data.frame(machine,failureTimeAll)
sampleData

# 기기별 평균값 구하기
tapply(sampleData$failureTimeAll, sampleData$machine, mean)
A B C D
36.0 16.0 15.2 38.4
# 기기별 표준편차 구하기
tapply(sampleData$failureTimeAll, sampleData$machine, sd)
A B C D
10.839742 7.106335 7.155418 8.264381

# 기기별 고장시간 boxplot
boxplot(failureTimeA, failureTimeB, failureTimeC, failureTimeD,
 main='기기별고장시간', xlab='기기', ylab='고장시간‘)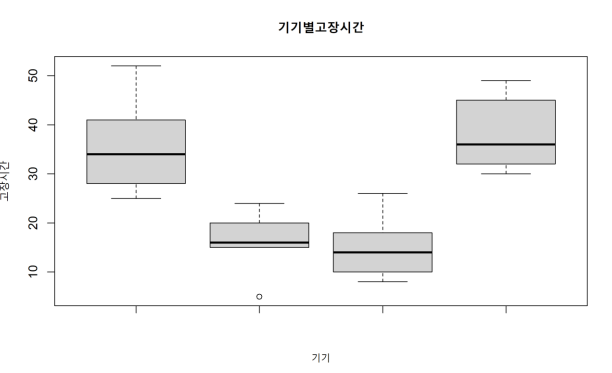

# Kruskal –Wallis 검정
kruskal.test(failureTimeAll ~ machine, data = sampleData)
Kruskal-Wallis rank sum test
data: failureTimeAll by machine
Kruskal-Wallis chi-squared = 13.834, df = 3,
p-value = 0.00314

6. R을 이용한 Friedman Test

• 세 개 이상의 집단을 비교하기 위한 방법, 요인이 두개

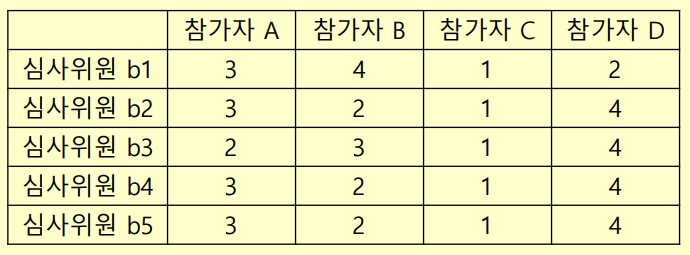
  다음은 콩쿨에서 5 명의 심사위원들이 4 명의 참가자를 대상으로 평가한 심
  사 자료이다. 참가자들의 점수에 유의한 사이가 있는지 검정하라
  

• 관련함수:
  friedman.test(x~group A \ block B,data=data이름)
  friedman.test(data$ y, data$ groupA, data$bIockB)

• y: 정량적인수치

• group A : a vector giving the group for the corresponding
  elements Of y

• block B : a vector giving the block for the corresponding
  elements Of y

# 점수 입력
y <- c(3,4,1,2,3,2,1,4,2,3,1,4,3,2,1,4,3,2,1,4)
# group에 해당하는 참가자 입력
groupA <- rep(c('A','B','C','D'),5)
# block에 해당하는 심사위원 입력
blockB <- c(rep('b1',4),rep('b2',4),rep('b3',4),rep('b4',4),rep('b5',4))

# Friedman 검정
friedman.test(y~groupA|blockB)
Friedman rank sum test
data: y and groupA and blockB
Friedman chi-squared = 10.68, df = 3, p-value =0.01359

7. Run Test

• 표본의 무작위성에 대한 검정
• 귀무가설 : 표본이 무작위로 추출되었다.

어떤 제품을 사용한 경험이 있는가를 알아보기 위해 26 명에게 물어보았다.
경험이 있는 경우는 C, 경험이 없는 경우는 D로 표기하였다. 이 표본이 무작위 추출이 되었는가를 검정하라.
DCCCCCDCCDCCCCDCDCCCDDDCCC

• 관련 함수: RunsTest(x, alternative="two.sided")
• Ⅹ: 정량적인 수치
• alternative : 검정관련 option ("two.sided"가 default, "less"
  "greater")

library(DescTools)
# 입력 data를 vector 형태로 받기
queue <- factor(c("d","c","c","c","c","d","c","c","d","c","c","c","c","d","c",
"d","c","c","c","d","d","d","c","c","c"))
# run 검정
RunsTest(queue, alternative="two.sided")
Runs Test for Randomness
data: queue
runs = 12, m = 17, n = 8, p-value = 1
alternative hypothesis: true number of runs is not equal the expected
number
# p-value=1 : 무작위로 추출된 표본이다.