문제

---

문제 분석

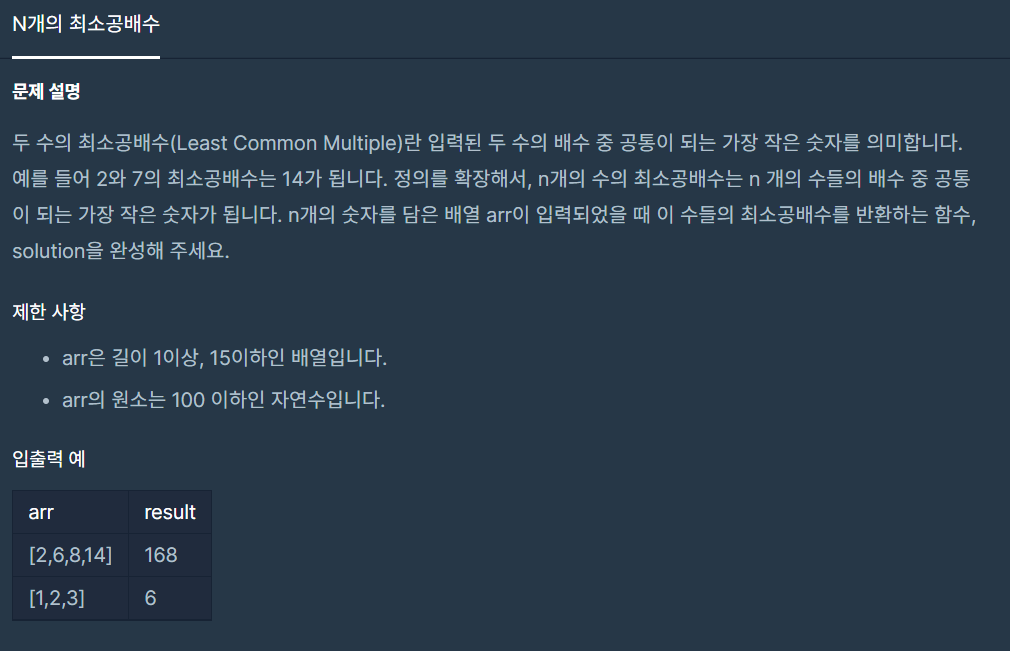
유클리드 호제법을 활용하여 GCD(최대 공약수)을 구하고 GCD를 활용하여 LCM(최소 공배수)을 구하는 문제다....
유클리드 호제법 https://namu.wiki/w/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C%20%ED%98%B8%EC%A0%9C%EB%B2%95

---

풀이

GCD(최대 공약수)

우선 GCD(최대 공약수)를 먼저 구현해야 한다. GCD를 구현해보자

public static int gcd(int a,int b){  //두 수를 입력 받음
        int r = 1; // 나머지 값
   
        while(b!=0){ //b가 0일때까지
            r = a % b; //a와 b를 나눈 나머지를 r에
            a = b; //a는 b의 값
            b = r;  //b는 r의 값
        }
        return a; //b기 0일때의 a가 최대공약수
    }

LCM(최소 공배수)

GCD를 활용하면 LCM을 쉽게 구할수 있다. 두 수를 곱한 수에서 최대 공약수를 나눠주면 최소 공배수이다.(예: 6,8은 각각 6=2x3, 8=2x2x2이므로 gcd=2 이고 lcm=24이다. 6x8/gcd(2)는 lcm(24))

public static int lcm(int a, int b){
        return a * b / gcd(a,b); //두 수를 곱한 값에서 gcd를 나눈다.
    }

---

코드

class Solution {
    public int solution(int[] arr) {
        int answer = 1;
        
        for(int i=0;i<arr.length;i++){
            answer = lcm(answer,arr[i]);
        }
        
        return answer;
    }
    
    
	public static int gcd(int a,int b){  //두 수를 입력 받음
        int r = 1; // 나머지 값

        while(b!=0){ //b가 0일때까지
            r = a % b; //a와 b를 나눈 나머지를 r에
            a = b; //a는 b의 값
            b = r;  //b는 r의 값
        }
        return a; //b기 0일때의 a가 최대공약수
    }
    
	public static int lcm(int a, int b){
        return a * b / gcd(a,b); //두 수를 곱한 값에서 gcd를 나눈다.
    }
}

---

GitHub

https://github.com/ds02168/Study_Algorithm/blob/master/%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%A8%B8%EC%8A%A4/%EC%9E%90%EB%B0%94/Level2/N%EA%B0%9C%EC%9D%98%20%EC%B5%9C%EC%86%8C%EA%B3%B5%EB%B0%B0%EC%88%98.txt