알고리즘 - Python

파이썬은 다른 프로그래밍 언어의 같은 데이터 타입만 모아 둘 수 있는 배열과 다르게 다른 데이터 타입들도 모을 수 있는 리스트(List)가 존재한다.리스트.append(요소) : 리스트의 마지막에 요소 추가리스트.pop() : 리스트의 마지막 요소 출력후 제거리스트.i

선형 탐색과 정렬, 이진 탐색에 대하여 알아보고 이진 탐색과 선형 탐색의 차이를 알아보았다. 성능면에선 이진 탐색이 선형탐색보단 뛰어났지만 항상 사용할 수 없는 단점이 존재한다.여러가지 옵션을 두고 선택할 수 있다.1.기존 리스트를 수정할지 새로운 리스트를 만들지2.오

재귀 알고리즘의 원리에 대해 알 수 있었다. 함수에서 종결조건에 다다를 때 까지 함수를 호출하고 합을 도출한다.와 같이 n부터 1까지의 합을 구할때 자기자신을 호출하여 구할 수 있을 것이다.이때 if n<=1 : return 1;과 같이 조건문 걸어두어 무한히 자

시간복잡도는 여러가지 기준에 따라 구분이 있다.시간에 따라 구분 할 것인지 <-> 공간에 따라 구분 할 것인지평균 시간에 따를 것인지 <-> 최악의 시간에 따를 것인지시간복잡도(Time Complexity) : 문제의 크기와 이를 해결하는데 걸리는 시간 간의

데이터 + 링크로 합쳐진 추상적 자료 구조다. 데이터는 값을 가지는 부분이고 링크는 다음 노드를 가리키는 주소이다. 크게보면 노드 -> 노드 -> 노드 ->....->노드 구조라고 생각하면 쉬울듯 하다.노드는 데이터와 링크로 이루어져 있다.연결리스트는 첫 노드를 가리키

이전의 단방향 연결리스트와 다르게 이전노드도 이어서 이동할 수있고, 헤드에만 더미노드를 넣었던 반면 tail에도 더미너드를 두어 좀더 수월하게 사이드 조건들을 처리할 수 있다.1.노드 구조2.리스트 구조3.달라진getAt4.insertAfter노드로 next와 더블어

스택 자료구조에 대한 강의, 자료를 넣고 빼고 확인할 수 있다. 배열로도, 이전에 배웠던 연결리스트로도 구현 가능선입 후출(LIFO)의 입출력을 가지는 자료구조로 스택의 top(가장 최근 자료를 가리킴)의 위치에 따라 늦게 들어온 순서대로 입력,삭제를 수행한다.http

연산자의 위치에 따라 중위연산자와 후위연산자에 대해 알아보고 중위연산자를 스택을 이용하여 후위연산자로 전환피연산자 연산자 피연산자 구조인 중위여산자와 달리 피연산자 피연산자 연산자 구조로 연산자가 가장 마지막에 위치함, 또 중위연산자와 달리 괄호를 사용하지 않아도 되는

후위연산은 중위연산과 다르게 괄호가 필요없고 좌측부터 순서대로 2개의 피연산자와 1개의 연산자를 차례대로 연산한다.1.중위연산자의 요소들을 뽑아내기2.중위연산자를 후위연산자로 전환3.후위연산자를 계산val을 주의해서 봐야한다 문자열로 숫자가 여러개 이어져있다고 가정하자

LIFO 입출력인 스택과 반대로 FIFO 입출력 형식인 큐(QUEUE)는 먼저 들어온 순서대로 출력된다. 즉 한쪽 방향으로 들어오고 나온다. 코딩테스트 문제를 풀면서도 스택은 본적이 몇번 있어도 큐는 잘 없던것 같다. 하지만 자주 사용되니 확실히 짚고 넘어가면 유익할듯

큐는 입력방향과 출력방향이 동일하기 때문에 스택과 다르게 자료의 크기가 커지거나, 오래 사용 될수록 O(n)이 커지는 단점이 존재한다. 이를 해결하기 위해 원형으로 큐를 이용하는것이 환형 큐(Circular Queue)이다.정해진 개수의 저장공간을 빙 돌아가며 이용하는

우선순위 큐는 일반적인 큐가 처리하는 순서인 FIFO와 다르게 우선순위에 따라 처리하는 데이터의 순서가 다릅니다.각각 다른 우선순위가 저장된 데이터들중 어느것을 먼저 실행하는지는 두단계에 선택적으로 선정될 수 있습니다.enqueue : 데이터가 저장될 때 우선순위에 맞

이진 트리는, 트리에 포함되는 모든 노드의 차수가 2 이하인 트리를 말합니다. 즉, 모든 노드는 자식이 없거나 (리프 노드의 경우), 하나만 있거나, 아니면 둘 있는 세 경우 중 하나에 해당합니다. 해당 노드의 노드수, 깊이를 출려해보고 순서에 따른 트리의 순회를 해봅

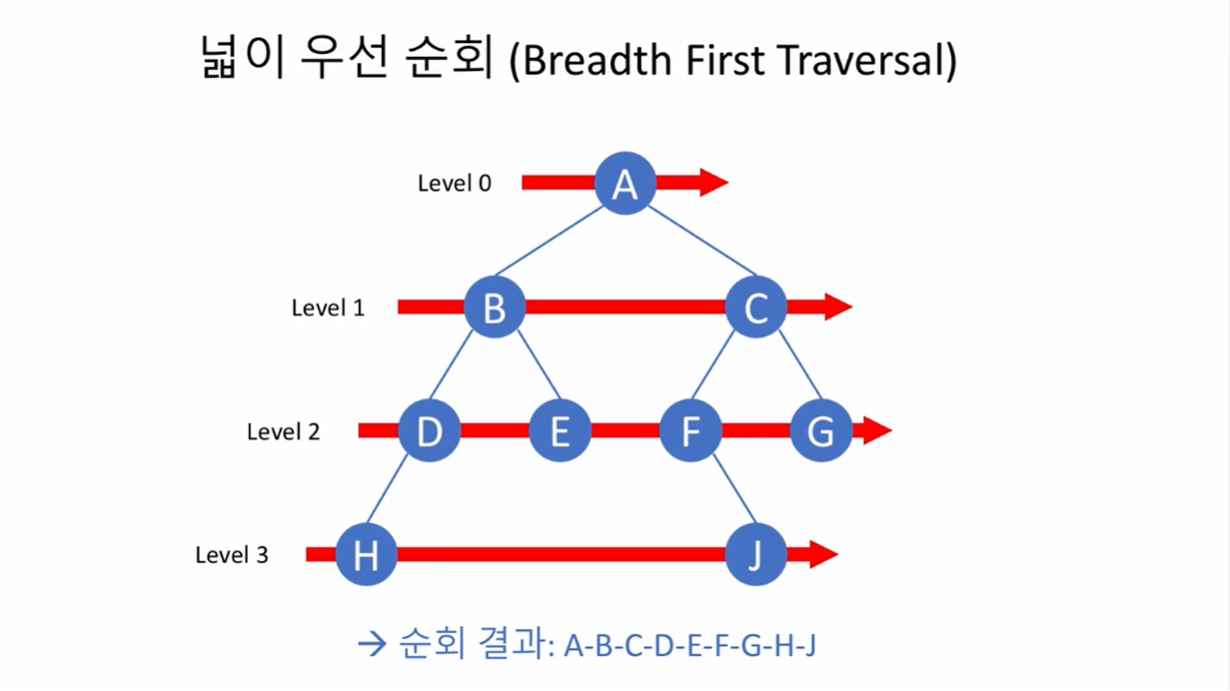
전,중,후위 탐색과 다르게 트리의 level별로, 또 같은 level에선 좌측노드부터 우측노드로 탐색 한다.큐를 이용하여 트리의 노드를 level별 순으로 방문 한다.순서에 맞게 정의 하면1\. 큐와 출력순서를 저장할 리스트 선언2\. 빈 트리일 경우 빈 리스트 출력3

이진트리의 탐색,삽입등을 구현해봄lookup() : 특정 원소를 검색 (탐색)max() : 최대 키를 가지는 원소를 탐색min() : 최소 키를 가지는 원소를 탐색insert() : 트리에 주어진 데이터 원소를 추가이진 탐색 트리의 원소 삽입 연산 구현이진 탐색 트리에

힙이랑 무엇인지, 또 어떻게 정렬되는지, 실제로 데이터를 삽입하고 힙을 유지시키기 위해 정렬 해봄이진 트리의 한 종류1\. 루트(root)노드가 언제나 최댓값 또는 최솟값을 가짐 \-최대 힙(max heap), 최소 힙(min heap)2\. 완전 이진 트리 여야 함힙