가장 큰 정사각형 찾기

유태형·2022년 2월 13일

코딩테스트 프로그래머스

프로그래머스 - Level 2

목록 보기

13/36

문제

문제 분석

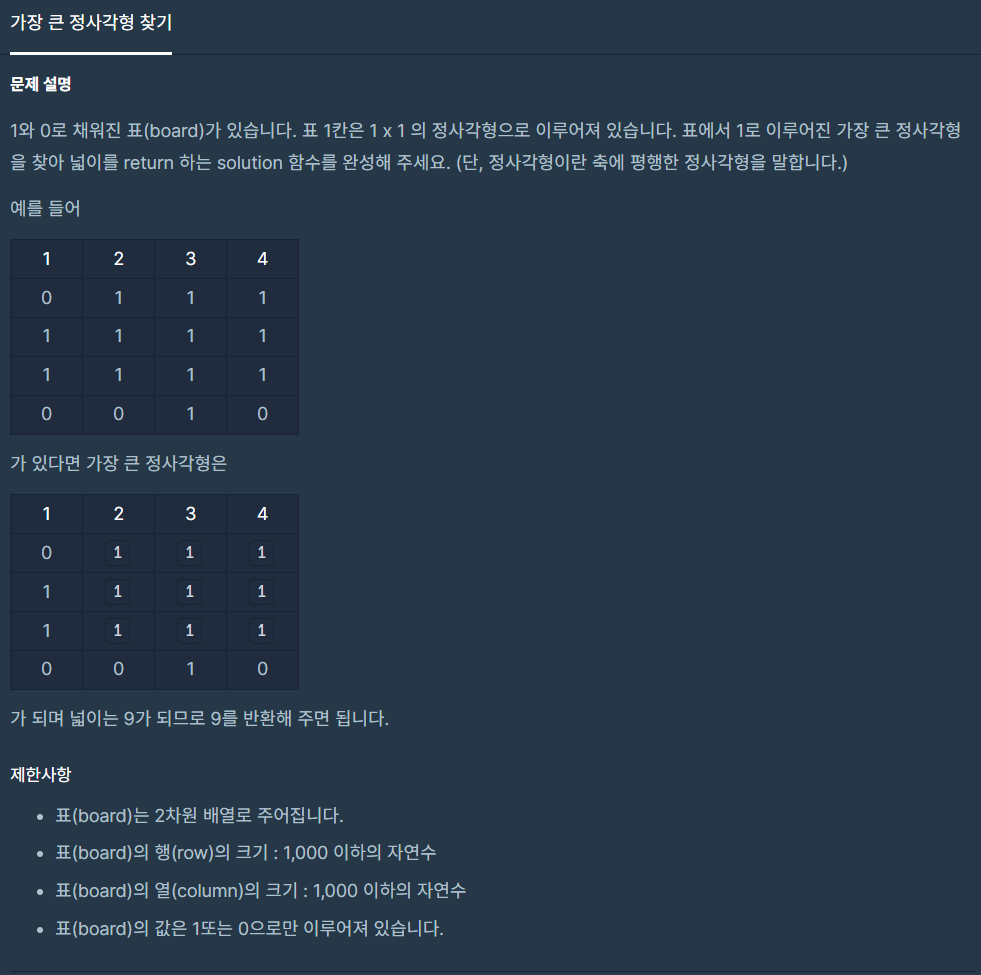
최대한 큰 1로 이루어진 정사각의 크기를 구하는 문제이다. 0이면 패스 1이면 점점 크기를 증가시켜가며 정사각형을 구성하고 있는지 체크 해야하므로 반복문이 아주 많이 겹칠것 같다.

풀이

효율성의 한계

for(행){
	for(열){
    	if(1일때){
        	for(행){
            	for(열){
                	정사각형 구분

1인 위치를 찾고 행과 열을 +1 씩 해 가며 정사각형 여부를 판단하였으나, if() break;문의 적극 활용에도 불구하고 효율성이 좋지 않았다.

Dynamic Programming

뒤에 나올 1들을 하나씩 세기보단 그전에 있었던 결과들을 비교하며 정사각형 여부를 확인하는것이 훨씬 빠를 것이다. 그러므로 이전 결과 + 현재 값으로 연산을 하는 다이나믹 프로그래밍이 필요하다.

	for(int i=1;i<board.length;i++){
       for(int j=1;j<board[i].length;j++){
           if(board[i][j] == 0) continue;
           board[i][j] = Math.min(Math.min(board[i][j-1],board[i-1][j]),board[i-1][j-1]) + 1;
           answer = Math.max(answer,board[i][j]);
       }
  	}

1.윗 셀, 왼 셀, 대각선 셀중 작은 값을 골라 +1 한다.
(우측아래 대각선으로 이동하며 이전결과(위,왼,대각)와 현재 값을 비교후 +1씩하며 정사각형 크기 가중치를 부가하는 동적 프로그래밍)
2.최대 값이면 바꾼다.

코드

class Solution
{
    public int solution(int [][]board)
    {
        int answer = 1;
        //모든 값이 0이면 0반환
        if(isAllZero(board)) return 0;
        
        for(int i =1; i< board.length; i++){
            for(int j = 1; j < board[i].length; j++){
                if(board[i][j] == 0) continue; //0이면 사각형 영역x
                //왼쪽, 위쪽, 대각선 중 최솟값에서 +1
                board[i][j] = Math.min(Math.min(board[i][j-1],board[i-1][j]),board[i-1][j-1]) + 1;
                //answer < board[i][j]면 바꿈
                answer = Math.max(answer,board[i][j]);
            }
        }
       
        //정사각형 넓이
        return answer * answer;
    }
    
    //0으로만 이루어진 배열
    private boolean isAllZero(int[][] board){
        for(int i = 0; i < board.length; i++)
            for(int j = 0; j < board[i].length; j++)
                if(board[i][j] == 1) return false;
        return true;
    }
}