피보나치 수

유태형·2022년 2월 8일

코딩테스트 프로그래머스

프로그래머스 - Level 2

목록 보기

4/36

문제

문제 분석

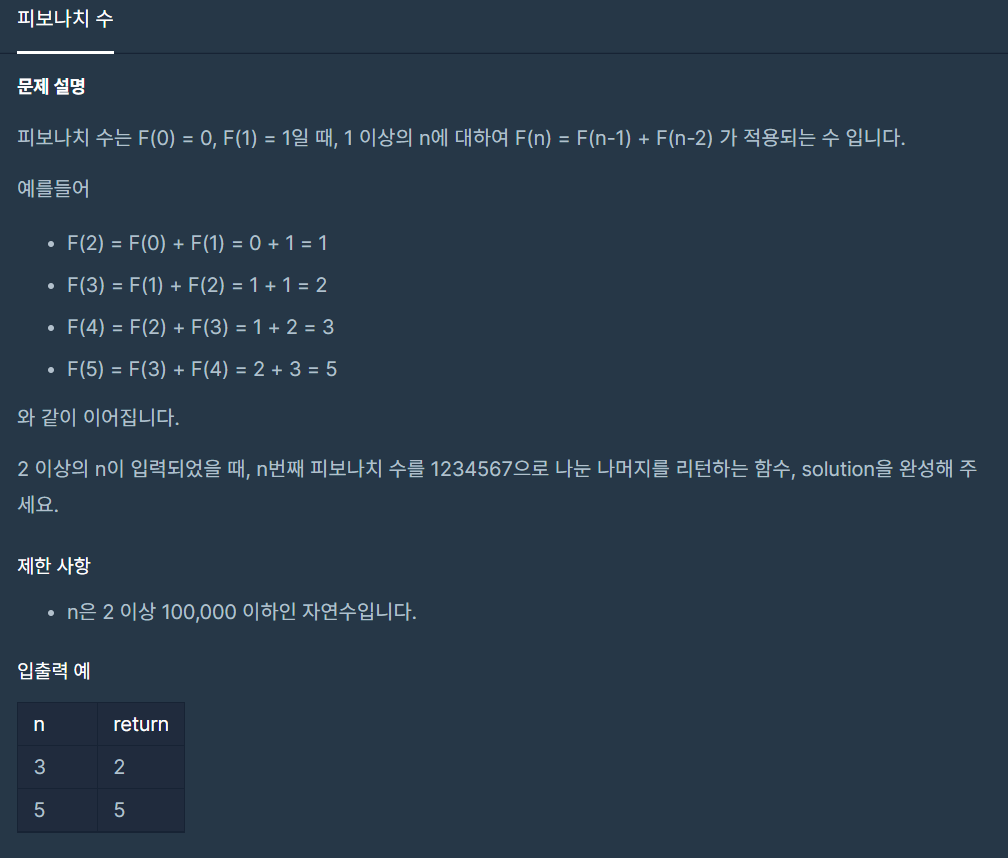
반복문을 이용하여 피보나치 수열을 구해야 하는 문제이다. 피보나치 수열은 0,1,1,2,3,5,8,13,....등 현재 값과 이전값을 더하여 다음값을 구하는 반복 수열 문제이다.

풀이

피보나치

반복문을 이용하여 피보나치 수열을 구해야 하므로

		int f0 = 0; //이전 값
        int f1 = 1; //현재 값
        int f2 = 1; //다음 값

로 변수를 선언하고

if(n < 2) //0,1일땐 n값 리턴
       return n;
   
   for(int i=2;i<=n;i++){ 
       f2 = f0 + f1 ; 
       f0 = f1;
       f1 = f2;
   }

for문으로 다음 값을 구해야 한다.

나머지

1234567로 나눈 나머지를 준 이유를 생각 해 봐야 한다.
나도 처음에 단순히 최종값에 나머지 연산만 했다가 오답나서 다른분이 공유한 정보를 보고 알았다.
https://programmers.co.kr/questions/11991
(정말 감사합니다 ㅠㅠ)

피보나치 수는 엄청나게 빠르게 증가하고 44번째만 되어도 int범위를 넘어 버린다.
즉. 44번째가 넘어가면 오버플로가 발생해서 연산이 무의미 해져버린다.
그래서 나머지를 일부러 넣어준 것이다.

(A+B+C+....+N) % X = ((A % X) + (B % X) + (C % X ) + ..... + (N % X)) % X

공식이 성립 한다.

0~1234566은 항상 int범위 안이다. 좌항의 A+B+C+....+N은 int범위가 벗어날 수 있지만 우항은 항상 0~1234566안의 수만 가지게 되므로 오버플로가 발생하지 않음을 보장할 수 있다.

for(int i=2;i<=n;i++){ //%1234567은 int와 long자료형으론 담아 낼 수 없다
       f2 = ((f0 % 1234567) + (f1 % 1234567)) % 1234567; //대신 더할때마다 
       f0 = f1 % 1234567; //%1234567하여 int자료형 내에서 나누어진다는걸 보장
       f1 = f2 % 1234567;
}

코드

class Solution {
    public int solution(int n) {
        int f0 = 0;
        int f1 = 1;
        int f2 = 1;
        
        if(n < 2) //0,1일땐 n값 리턴
            return n;
        
        for(int i=2;i<=n;i++){ //%1234567은 int와 long자료형으론 담아 낼 수 없다
            f2 = ((f0 % 1234567) + (f1 % 1234567)) % 1234567; //대신 더할때마다 %1234567하여 int자료형 내에서 나누어진다는걸
            f0 = f1 % 1234567; //보장
            f1 = f2 % 1234567;
        }
        
        return f2;
    }
}